7.2 Перевірка лінійної регресії.

Позначимо через частинне середнє, що відповідає j-тому значенню пояснювальної змінної:

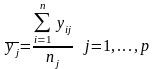(47) де 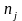- число значень y, що відносяться до x_jk ( );

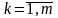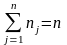.Знайдемо тепер сер. квадр. відхилень y_ij від їх частинних сер.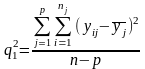 (48)

Показник(48)є мірою розсіювання дослідних даних навколо своїх частинних середніх,тобто мірою, що не залежить від вибраного вигляду регресії.В якості міри розсіювання дослідних даних навколо емпір. регрес. прямої вибирається сер. квадр. відхилень: (49)

Обидва показники 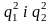є незалежними статистичними оцінками однієї і тієї ж дисперсії 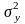. Якщо 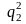не набагато більше 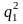, то в якості гіпотетичної залежності може бути взята лінійна.

Якщо в генеральній сукупності існує лінійна регресія і умовні розподіли змінної y хоч би приблизно нормальні, то відношення середній квадратів 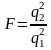(50)

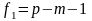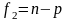має F розподіл з і степенями вільності.

Значення F пораховане за формулою (50) порівняне з критичним 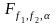знайденим за таблицею F-розподілу при заданому рівні значущості і 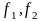степенями вільності. Якщо 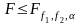, то різниця між обома середніми квадратами відхилень статистично незначна і вибрана нами лінійна регресійна залежність може бути прийнята, як правдоподібна.

7.3 Розв’язок задач у випадку порушення класичних припущень(мультиколінеарність)

При вивченні матричної лінійної регресії часто зустрічаються з наявністю лінійного зв’язку між всіма чи деякими пояснювальними змінними. Це явище називається мультиколінеарністю.

1. Для вимірювання стохастичної мультиколінеарності можна використати коефіцієнт множинної детермінації. При відсутності кореляції між пояснювальними змінними, тобто при відсутності мультиколінеарності, коефіцієнт множинної детермінації дорівнює сумі відповідних коефіцієнтів парної детермінації: 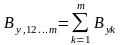(51)

При наявності мультиколін. співвідношення(1)не виконується.Тому в якості міри мультиколін. можна запропонувати різницю: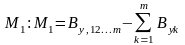 (52)

Чим менша ця різниця, тим менша мультиколінеарність.

2. Інший показник базується на використанні для вимірювання мультиколін.чисельн. формули коеф. множи. детермінації.

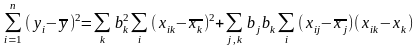
для 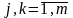, 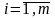(53) Вираз 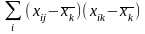(54)

є чисельником формули коефіцієнта парної кореляції між змінними 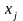та 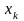. При відсутності колінеарності загального показника мультиколінеарності можна використовувати різницю М₂:

(55)

3. Також в якості показника мультиколінеарності можна також використати вираз (52), розділивши його на 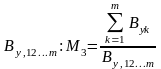(56)

Чим більше М₃, тим інтенсивніша мультиколінеарність.

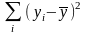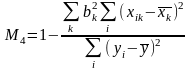4. Відомий показник мультиколінеарності, отримують з формули (5). Розділивши праву і ліву частини формули на , отримаємо: (57)

Розроблені ряд методів виключення чи зменшення мультиколінеарності:

• виключення змінних;

• лінійне перетворення змінних;

• виключення тренду;

• використання попередньої інформації;

• покрокова регресія;

• метод головних компонентів.

Якщо зменшити мультиколінеарність не вдається, то до оцінок коефіцієнтів регресії і до значень регресії треба відноситись з великою обережністю.