
- •Етапи аналізу даних.
- •Класифікація типів змінних.
- •Залежні змінні і незалежні.
- •Групування даних.
- •Етапи попередньої обробки даних .
- •2.2 Числові характеристики вибірки.
- •2.3 Перевірка основних гіпотез.
- •Видалення аномальних спостережень.
- •Перевірка випадковості (стохастичності) вибірки.
- •Графічне представлення даних.
- •3.1. Суть кореляційного аналізу
- •3.2 Коефіцієнт детермінації – це є квадрат коефіцієнта кореляції, долю варіації, спільну для двох змінних, іншими словами “степінь” залежності двох змінних.
- •3.3 Частинні коефіцієнти кореляції.
- •3.4. Нелінійна кореляція.
- •4.1 Коефіцієнт рангової кореляції.
- •4.2 Індекс Фехнера.
- •4.3. Кореляційне відношення Пірсона
- •4.4.Коефіцієнт конкордації.
- •Тема: „Регресійний аналіз”.
- •Регресійний аналіз – сукупність статистичних методів, що орієнтовані на дослідження стохастичної залежності однієї змінної y від набору інших змінних .
- •.1Метод найменших квадратів
- •6.1.2 Алгоритм ручного рахунку:
- •6.2 Лінеаризації у випадку криволінійних залежностей
- •6.3 Визначення параметрів парної лінійної регресії для згрупованих даних
- •6.4 Множинна лінійна регресія
- •7.2 Перевірка лінійної регресії.
- •7.3 Розв’язок задач у випадку порушення класичних припущень(мультиколінеарність)
- •Дисперсійний аналіз
- •8.3 Модель 1. Однофакторний дисперсійний аналіз
- •8.4 Двофактоний да
- •8.4.1 Загальна схема двофакторного дисперсійного аналізу(перехідна класифікація з повтореннями)
- •8.4.2 Модель іі
- •Модель ііi.
- •9.1 Коваріаційний аналіз.
- •III. Перевірка гіпотези в умовах ;
- •10.1 Поняття класифікації, задача класифікації
- •10.2. Основні поняття кластерного аналізу та їх застосування
- •10.3 Типи відстаней і мір подібностей
.1Метод найменших квадратів
Графічно цю задачу можна представити так – у полі розсіювання ( xi, yi) площини хоу необхідно провести пряму так, щоб величина всіх відхилень відповідна умові :
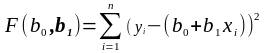 (9)
(9)
Тому цей метод регресійного аналізу називається методом найменших квадратів (МНК).
Для знаходження коефіцієнтів залежності (8), необхідно знайти часткові похідні по b0 та b1 від функції (9) і прирівняти їх до нуля
 (10)
(10)
Після простих перетворень отримаємо систему нормальних рівнянь:
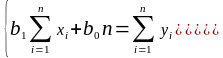 (11)
(11)
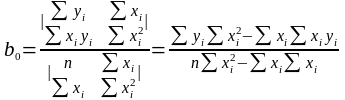 (12)
(12)
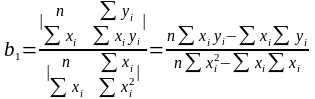 (13)
(13)
Визначивши b0 та b1, можна по (8) обчислити значення регресії для заданої області пояснювальної змінної х.
Зауваження. На практиці коефіцієнти b0 та b1 частіше знаходять з використанням коефіцієнтів кореляції та коваріації.
6.1.2 Алгоритм ручного рахунку:
1) знаходимо середні значення масивів Х та У:
 ,
,
 (14)
(14)
2) знаходимо вибіркові відхилення:
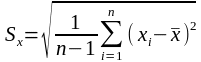 ,
,
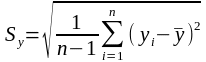 (15)
(15)
3) знаходимо коефіцієнт коваріації:
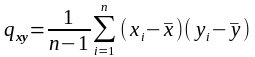 (16)
(16)
4) знаходимо коефіцієнт кореляції:
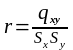 (17)
(17)
5) знаходимо коефіцієнт рівняння регресії:
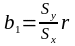
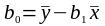 (18)
(18)
6) знаходимо теоретичні значення змінної У:
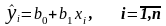 (19)
(19)
7)
знаходимо
середнє відхилення, смугу відхилення
та інтервал довір’я:
 (20)
(20)
 - смуга;
- смуга;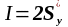 (21)
(21)
6.2 Лінеаризації у випадку криволінійних залежностей
На практиці дуже часто зв’язок між двома параметрами носить нелінійний(криволінійний) характер. У більшості випадків за допомогою простих перетворень можна нелінійну залежність до лінійної, тобто провести лінеаризацію.
6.3 Визначення параметрів парної лінійної регресії для згрупованих даних
Для кореляційної таблиці, яку розглянули раніше, мають місце наступні співвідношення:
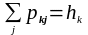
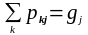 (23)
(23)
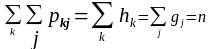 (24)
(24)
Середні
значення
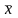 та
та
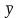 визначаються, як середні зважені за
серединами інтервалів:
визначаються, як середні зважені за
серединами інтервалів:
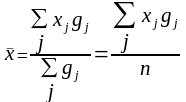 (25)
(25)
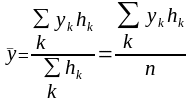 (26)
(26)
Шляхом заміни в (12) і (13) окремих значень хі та уі серединами інтервалів, що зважені за відповідними частотами, отримаємо формули для обчислення оцінок параметрів за згрупованими дуними:
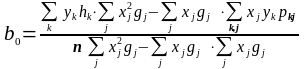 (27)
(27)
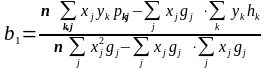 (28)
(28)
6.4 Множинна лінійна регресія
При існуванні лінійного співвідношення між змінними, загальний вираз рівняння множинної регресії (1) записується у вигляді:
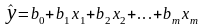 (29)
(29)
Підставляючи (34) в (30) маємо:
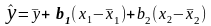
або (35)
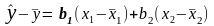
З системи нормальних рівняннь отримуємо b0 та b1:
 (36)
(36)
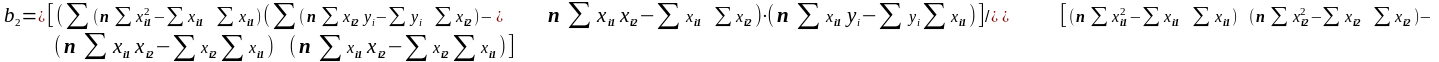 (37)
(37)
(Хз)Загальна процедура проведення регресійного аналізу включає в себе наступні етапи:
Формулювання економічної проблеми. На даному етапі формулюються гіпотези про залежність економічних явищ. Потім залежність кількісно оцінюється за допомогою методів регресійного аналізу, а саме яку форму і який вид може дана залежність.
Ідентифікація змінних. Визначають найбільш оптимальну кількість змінних, і класифікують їх на залежні і пояснювальні змінні.
Збір статичних даних. Приймається рішення про проведення досліджень за всією генеральною сукупністю чи за її вибіркою. Після цього приступають до збору даних для кожної змінної, включеної в аналіз.
Специфікація функції регресії. На цьому етапі дослідження, висувається конкретна гіпотеза про форму зв’язку.
Оцінка функції регресії. Визначаються числові значення параметрів регресії. Крім того, обчислюється ряд статичних показників, що характеризують точність регресійного аналізу.
Оцінка точності регресійного аналізу. На цьому етапі повинні бути зроблені висновки про точність результатів.
Економічна інтерпретація. Результати регресійного аналізу порівнюються з гіпотезами, що були сформульовані на першому етапі дослідження, і оцінюється їх правдоподібність з економічної точки зору.
Передбачення невідомих значень залежної змінної(прогноз).
