4.2 Індекс Фехнера.

Ще одним простим показником ступеня взаємозв’язку між двома статистичними рядами є індекс Фехнера. Для його визначення по кожному ряду обчислюють середні 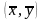, і визначають знаки відхилень 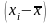та 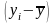. Позначимо через v кількість співпадань, а через w- кількість неспівпадань знаків різниць. Індекс Фехнера і визначається за формулою

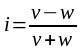(7)

Відхилення, що дорівнюють 0, відносять пополам до v і до w. Легко переконатись, що 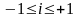. При і>0 маємо додатню кореляцію, а при і<0 – від’ємну, а при і=0 зв’язок відсутній.

Первага індекса Фехнера- простота обчислень. Але великий недолік в тому, що він враховує тільки кількість співвідношень і неспівпадань знаків відхилень. Тому рекомендується лише для приблизної оцінки зв’язку.

4.3. Кореляційне відношення Пірсона

Для вимірювання тісноти зв’язку між двома явищами використовується кореляційне відношення 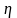запропоноване Пірсоном.

Процедури обчислень кореляційного відношення та індекса кореляції дуже схожі. Відмінність полягає в тому, що при обчисленні кореляційного відношення виходять із частинних середніх, а не з відповідних значень регресії.

Кореляційне відношення Пірсона

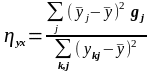
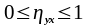(8)

g_j – частота j-ї групи (інтервала) значень змінної х, j=1,2,…,t.

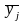- частинне середнє змінної у для j-ї групи (інтервала) значень пояснювальної змінної х;

у_kj - k-те значення залежної змінної у в j-й групі (інтервалі) значень пояснювальної змінної х, k=1,2,…,5.

Якщо числовий матеріал поданий у вигляді кореляційної таблиці, то на практиці зручно користуватись формулою:

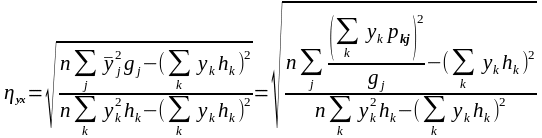(9)

.

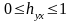
Частіше всього кореляційне відношення тим більше, чим більш дифиренційоване групування по залежній змінній. Оскільки при обчисленні виходять із середніх, тому очевидно, що .

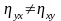4.4.Коефіцієнт конкордації.

В економіці існує велике число явищ, ознаки яких не піддаються точній кількісній оцінці. Це так звані атрибутні ознаки. Наприклад, професія, форма власності, якість виробу, техноолгічні операції і так далі. Дослідник ранжирує елементи сукупності, приписуючи кожному з них порядковий номер, що відповідає підсумкам порівнянь по даній ознаці з іншими елементами. Якщо кількість ознак- змінних більше двох, то в результаті ранжировок п елементів (підприємств чи установ) мають справу з т послідовностями рангів. Для перевірки, чи добре узгоджуються ці т ранжировок одна з одною, використовують коефіцієнт конкордації Кендела:

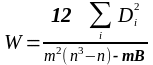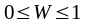(10) , (11)

При наявності зв’язних (об’єднаних рангів) коефіцієнт конкордації W обчислюється за формулою(11): де 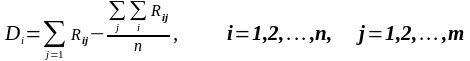(12)

j – сума рангів, приписаних всіми експертами і-му елементу вибірки, мінус середнє значення цих сум рангів;

т – число експертів чи ознак, зв’язок між якими оцінюється;

п - об’єм вибірки (кількість підприємств чи установ), іншими словами, це кількість членів послідовності рангів;

, В_k – число зв’язаних рангів, k=1,…,z.

Коефіцієнт W приймає значення: .

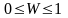Тема: „Регресійний аналіз”.

5.1 Поняття регресії.

Регресія – це одностороння стохастична залежність. Вона встановлює відповідність між випадковими змінними.

Одностороння стохастична залежність виражається за допомогою функції, яка, для відмінності її від строго математичної функції, називається функцією регресії або просто регресією.

види регресії:

1. Відносно числа явищ (змінних), що враховуються в регресії, розрізняють:

   • просту регресію (між двома змінними);

   • множинну чи частинну регресію (між залежною змінної у і декількома (пояснювальними) незалежними змінними х₁,х₂,...,х_m).

2. Відносно форми залежності розрізняють:

   • лінійну регресію, що виражається лінійною функцією;

   • нелінійну регресію, виражається нелінійною функцією.

3. В залежності від характеру регресії розрізняють:

   • додатну регресію (якщо із збільшенням чи зменшенням значень пояснювальної змінної значення залежної змінної також відносно від’ємну регресію збільшуються чи зменшуються).

4. Відносно типу з’єднань явищ розрізняють:

   • безпосередню регресію (явища з’єднані безпосередньо між собою);

   • опосередковану регресію (пояснювальна змінна діє на результативну змінну через деяку третю або через ряд інших змінних);

   • нонсенс-регресію (хибна або абсурдна регресія).