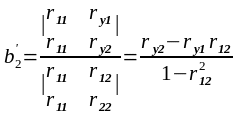4. Видалення аномальних спостережень.

Видалення спостережень, величина яких не порівнюються (узгоджуються) з розподілом основної маси даних.

Ідентифікація аномальних спостережень дозволяє ще раз перевірити умови їх реєстрації і тим самим знайти і виправити помилку. Якщо ж помилку виправити не вдається, то дані просто виключаються із подальшої обробки як нетипові.

Розглянута задача поділяється на два етапи:

1. Вияв „підозрілих” спостережень;

2. Перевірка статистичної значимості їх відмінності від основного набору даних

4. Перевірка випадковості (стохастичності) вибірки.

Для перевірки, чи вибірка випадково вибрана із нормальної генеральної сукупності, чи вибірка випадково вибрана із нормальної генеральної сукупності, чи незалежні нормально розподілені випадкові величини, можна скористатись критерієм Аббе. Статистика критерія підраховується за формулою: .

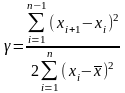4. Графічне представлення даних.

Гістограма служить для зображення варіаційного ряду розподілу, полігон – для дискретного варіаційного ряду.Для побудови графіка емпіричної щільності ймовірності на кожному інтервалі, як на основі, будують прямокутник, площа якого дорівнює або числу випадків, або відносній частоті. Графіки такого вигляду називають гістограмами. Іноді замість гістограми будують полігон, який отримують із гістограми якщо з'єднати відрізками прямих середини верхніх сторін прямокутника

3.1. Суть кореляційного аналізу

Кореляція – це залежність між двома випадковоми величинами. Вона характеризується коефіцієнтами кореляції.

Кореляційний аналіз полягає у визначенні тісноти зв’язку між двома випадковими величинами.

Тіснота лінійного зв’язку в кореляційному аналізі характеризується спеціальним відносним показником, який називається коефіцієнтом кореляції. Значення коефіцієнта кореляції р належить відрізку [-1,1]. Якщо 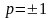, то між випадковими величинами існує лінійний функціональний зв’язок. Якщо р=0, то між величинами x і y кореляції немає і їх називають некорельованими. Якщо р=1, то зв’язок називається функціональним. Для нормально розподіленої сукупності x і y некорельованість означає, що величини x і y незалежні. Додатний знак р вказує на прямий зв’язок між x і y, а від’ємний – на обернений зв’язок. Чим ближче коефіцієнт кореляції до одиниці, тим зв’язок між x і y тісніший.

вибірковим коефіцієнтом кореляції, його позначають r і обчислюють за формулою

(1)

Значення r_xy=0 говорить про відсутність лінійного зв’язку, можливо існує тісний нелінійний зв’язок, навіть нелінійний функціональний.

Для перевірки нульової гіпотези обчислюють статистику 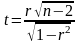, де п-обсяг вибірки. Статистика t має розподіл Стьюдента з степенями вільності. Обчислене за формулою (3) значення t-критерію порівнюють порівнюють з критичним значенням , знайденим за таблицею розподілу Стьюдента при заданому рівні значущості і числі ступенів вільності .

3.2 Коефіцієнт детермінації – це є квадрат коефіцієнта кореляції, долю варіації, спільну для двох змінних, іншими словами “степінь” залежності двох змінних.

Коефіцієнт множинної кореляції характеризує тісноту зв’язку однієї змінної із сукупністю інших.

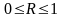(7)

де r_і – парні лінійні коефіцієнти. По аналогії з парною кореляцією:R²- коефіцієнт детермінації.

З допомогою коефіцієнта множинної кореляції не можна зробити висновок про характер взаємозв’язку, тобто про додатність чи від’ємність кореляції між змінними.

Формула коефіцієнта множинної кореляції для будь-якого числа змінних має вигляд:

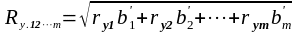, де (9)

,
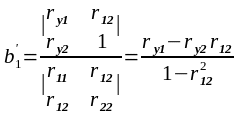