III. Перевірка гіпотези в умовах ;
.
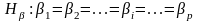Суми квадратів „між групами” і „всередині груп” повинні бути скореговані так, щоб вплив незалежної змінної z було б виключено:
а=а1+а2 ; b=b1+b2 ; c=c1+c2 (14)
Відповідно:
;
; 
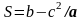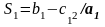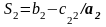(15)
Статистика
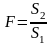в
умовах гіпотези
має
F-розподіл
з
f1=p-1,
f2=N-p-1
степенями
вільності.
Розглянуту схему можна узагальнити на випадок, коли класифікація спостережень виконана за двома і більше факторами.
10.1 Поняття класифікації, задача класифікації
Під терміном класифікація розум розподіл предметів за заг. класами згідно най б. суттєвих ознак, які притаманні предметам даного типу і які відрізняють їх від предметів інших типів. Правила класифік: 1. в одній класиф. викор. Одна основа; 2. об’єм класу = сумі об’ємів підкласів коли і підкласи пересікаються; 3. поділ на підкласи пр неперервно.
Задачі класифік: 1. Виявлення природного розп. вихідних спостережень на чітко виражені групи. 2. Типізація, при якій об’єкти розбиваються на порівняно невелику к-сть обл.. групування
Класиф. об’єктів можна пров. за допомогою якісних , кількісних і інших ознак. Викор-ся формальні мат. Методи розбиття на класи є експериментальним метод, при якому розб. на класи проводять спеціалісти з однієї області, використовуючи проф. знання, доск.
Кластерний аналіз – це сукупність методів, але розбиття спостер. на однорідні групи. Техніка класиф. викор. в різних областях.
Задачі класт. аналізу є 2-х видів:за об’ємом – класиф. відносно невеликих за об’ємом сукупностей; -класиф. великих об’ємів багатовимірних спостережень.
Задачі класиф. ділять за типом апріорної інф-ції: 1. кількість класів задана; 2. кількість класів невідана і її треба визнач.; 3. кількість класів непотрібна.
Дерева – агломеративне та дивизивне
10.2. Основні поняття кластерного аналізу та їх застосування
Виділяють 3 основні кластерні процедури: 1. ієрархія алгоритмів ідомезивні;2. паралельна процедура за допомогою ітераційних алгоритмів; 3. послідовні процедури з малою кількістю спостережень.
Кластер – накопичення, група елементів, які хар-ся деякою заг. властивістю, методи їх знаходження і є кластер ний аналіз.
Таксон – систематизована група б-я категорії, методи їх знаходження назив. чисельною таксономією.
Матричний простір – пара (х,d), яка склад-ся з деякої множини елементів простору Хі і відстані d.
Функція відстані – однозначна, невідємна, дійсна ф-ція для якої викон-ся аксіоми: 1. d(xu, xs)≥0; 2. d(xu, xs)=0 – максимальна близькість елементів з самим собою, коли xu=xs; 3. d(xu, xs)= d(xs, xu,) – симетрія; 4. d(xu, xs)≤ d(xu, xz)+ d(xz, xs).
Міра подібності - однозначна, невідємна, дійсна ф-я Г(xu, xs), яка визначена для б-я xs, якщо виконується аксіома: а). 0≤ r(xu, xs)<1, б-я xu≠xs; б). r(xu, xs)=1, xu=xs; в). r(xu, xs)= r(xs, xu), г). d(xs, xv)>d(xu, xs) =>r(xz, xv)≤ r(xu, xs).
10.3 Типи відстаней і мір подібностей
Агломеративна кластерна процедура пов’язана з обчисленням міри між всіма парами об’єктів і обєдн. на кожному кроці тієї пари для якої досягається min і max даних ф-й. Кластиризація здійснюється шляхом обєднаня спочатку роз’єднаних к об’єктів.
Дивизивна кластерна процедура. пов’язана з обчисленням мір залежності між парами об’єктів і виділенням на кожному кроці тієї пари об’єктів для якої досягається min max даних ф-й. Кластер. здійснюється шляхом розбиття однієї групи об’єктів.
Коефіцієнт подібності чи відмінності між і-ми спостереженнями діляться на 3 типи:
dr
(xut
,xst
)=(
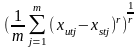);коеф.
відстані;
r(xut,xst
)=
коеф.
асоц.
r
=
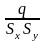.Коеф.
кореляції
10.4 Дискримінантний аналіз. Методи дискр. аналізу виробл. деякі виріш. правила, що дозв. віднести запропоновані об’єкти до заданих класів. Вирішальні правила можуть бути стр. у вигляді ймов. (метод Баєса); простих функ. класиф. як у лін. дискр. анал. Фішера. Дискримін. ф-цій; у вигляді деяких характеристик; у вигляді ваг і зміщень нейронів.