8.4 Двофактоний да

Складнішою моделлю дисперсійного аналізу є вивчення впливу на результати експерименту кількох факторів. Зокрема при аналізі впливу двох факторів структура моделі набуває вигляду:

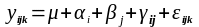(27)

де, 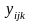- значення ознаки y в і-му експеременті j-му рівні впливу фактора А і на k-му рівні впливу фактора В; -загальна середня величина ознаки у; 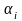-ефект впливу факторів А на і-му рівні,

-ефект впливу фактора В на j-му рівні;

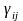-ефект одночасного впливу факторів А і В;

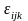-випадкова компонента ( варіація в середині окремої групи ).

В двофакторному аналізі розрізняють багатосторонню (перехресну) класифікацію, коли таблиці вхідних даних 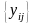кожний j-й стовпець (j-та градація фактора В) містить однакову кількість груп, що відповідають градаціям і-го фактора А, та ієрахічну класифікацію, коли фактор В (другосторонній в рамках даної задачі) згрупований всередині головного А. В ієрархічній класифікації число градацій фактора В, що фіксуються всередині різних градацій фактора А, може бути поодиноким.

В умовах моделі 1 фактори А, В, 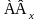розглядаються, як фіксовані, щодо моделі 2 – як випадкові. Для змішаної моделі одному із факторів приписується систематичний вплив, другому випадковий. Для визначеності, допускають, що в моделі 3 фактор В- фіксований, а фактор А, і їх взаємодія АВ- випадковий.

8.4.1 Загальна схема двофакторного дисперсійного аналізу(перехідна класифікація з повтореннями)

1. обчислюються вибіркові середні:

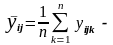середнє значення ознаки у для кожного блока; (28)

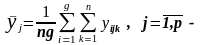середнє значення ознаки у за (29)

стовпцями;

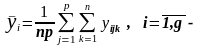середнє значення ознаки у за (30)

рядками;

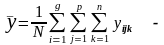загальна середня ознаки у (31)

де .

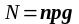2. Визначаються суми квадратів відхилень, що обумовлені впливом різних факторів:

а) 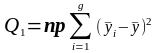- вплив фактору А; (32)

б) 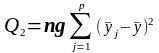- вплив фактору В; (33)

в) - вплив взаємодії факторів АВ; (34)

г) 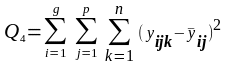-зміни, пов’язані з (35) відмінностями всеридині комірки;

д) 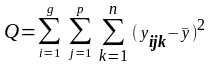-загальна зміна, даної ознаки. (36)

Справедлива рівність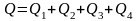 . Величина відповідає (g-1)-степеней вільностей;

.

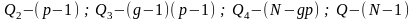3.Тепер неважко знайти середні квадрати відхилень:

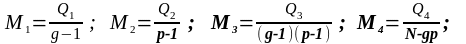(37)

Перевірка гіпотез

Модель 1.

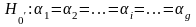
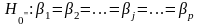
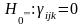
Перевірка гіпотез здійснюється за критерієм:

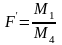
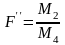
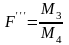
Якщо 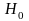вірна то дані величини підлягають F розподілу.

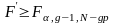
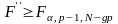
Якщо виконується то вплив відповідно факторів а,в і їх взаємодія вважаються суттєвими.

8.4.2 Модель іі

Нульові гіпотези, що перевіряються запишемо так:

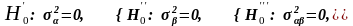(41)

Відповідні критерії мають вигляд:

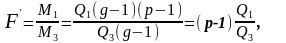
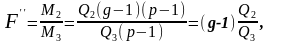
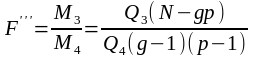,(42)

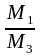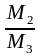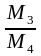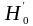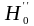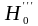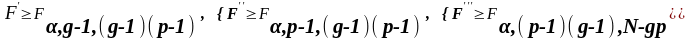В умовах нульової гіпотези відношення , і мають F-розподіл з відповідними степенями вільності. Гіпотези , , відхиляються (при заданому рівні значущості ), якщо (43)