2. Постановка задачи

Необходимо решить задачу отражения земных радиоволн , падающих под произвольным углом на плоскую границу льда, расположенного на морской воде . Границы между средами считаем плоскими. Задача можно рассматривать в двух случаях.

1. При температуре воздуха выше – 22 градуса в морском льду не происходит кристаллизация хлорида натрия, и лед имеет существенно поглощение , относительно стабильное по толщине льда. ,тот слой вносит основной вклад в ослабление .

2. При температуре воздуха ниже -22 градуса верхний слой льда теряет хлорид натрия, создавая слой приближающийся по электромагнитным характеристикам к пресному льду с малыми потерями.

Рассмотрим первую( основную) задачу.

На рисунке 2.1 приведена модель данной среды распространения земных радиоволн, а та же показан процесс падения. Заметим, что задачу мы рассматриваем для горизонтальной поляризации!

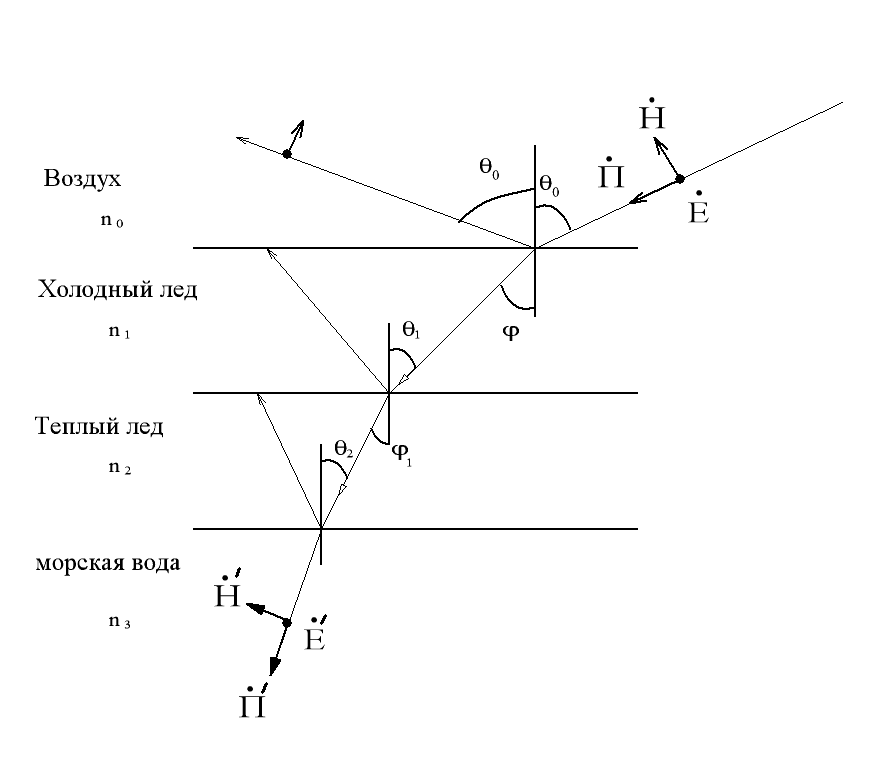
Рис. 2.1. Падение радиоволны под произвольным углом на границу раздела сред, с последующим распространением в двух средах

Каждую границу раздела можно представить как эквивалентный четырехполюсник, со своими коэффициентами передачи и отражения.

На рис.2.2 показана структурная схема, где границами сред являются четырехполюсники. Граница между средами воздух и холодный лед - четырехполюсник -1, между холодный лет и теплый лед – четырехполюсник -2. Граница между средами теплый лед - вода, является нагрузкой, для данного каскадного соединения четырехполюсников.

Длина линий между четырехполюсниками и четырехполюсником-2 и нагрузкой, это физический путь волны в среде, т.е. расстояние, которое проходит радиоволна в каждой среде.

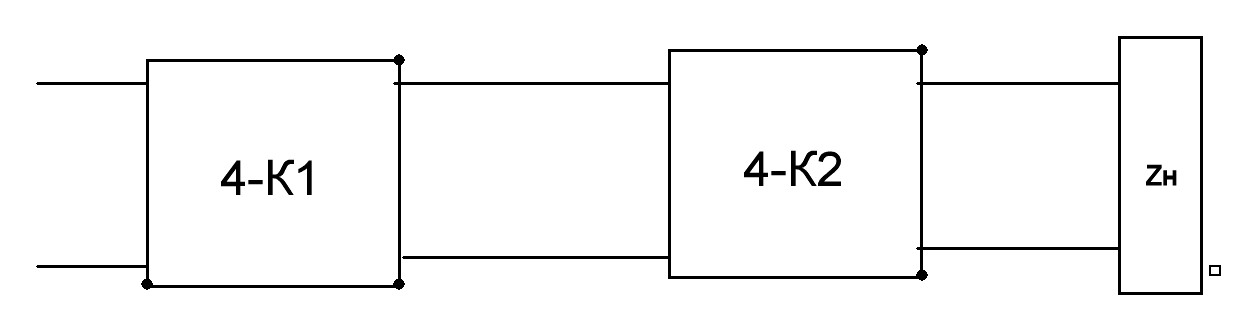
Рис.2.2. Структурная схема физической среды

3 Математическая модель физической структуры

Теперь можно непосредственно приступить к математическому описанию данной физической структуры. Заменим структурную схему направленным графом и обозначим соответствующие коэффициенты отражения на зажимах четырехполюсника, а также коэффициенты передачи.

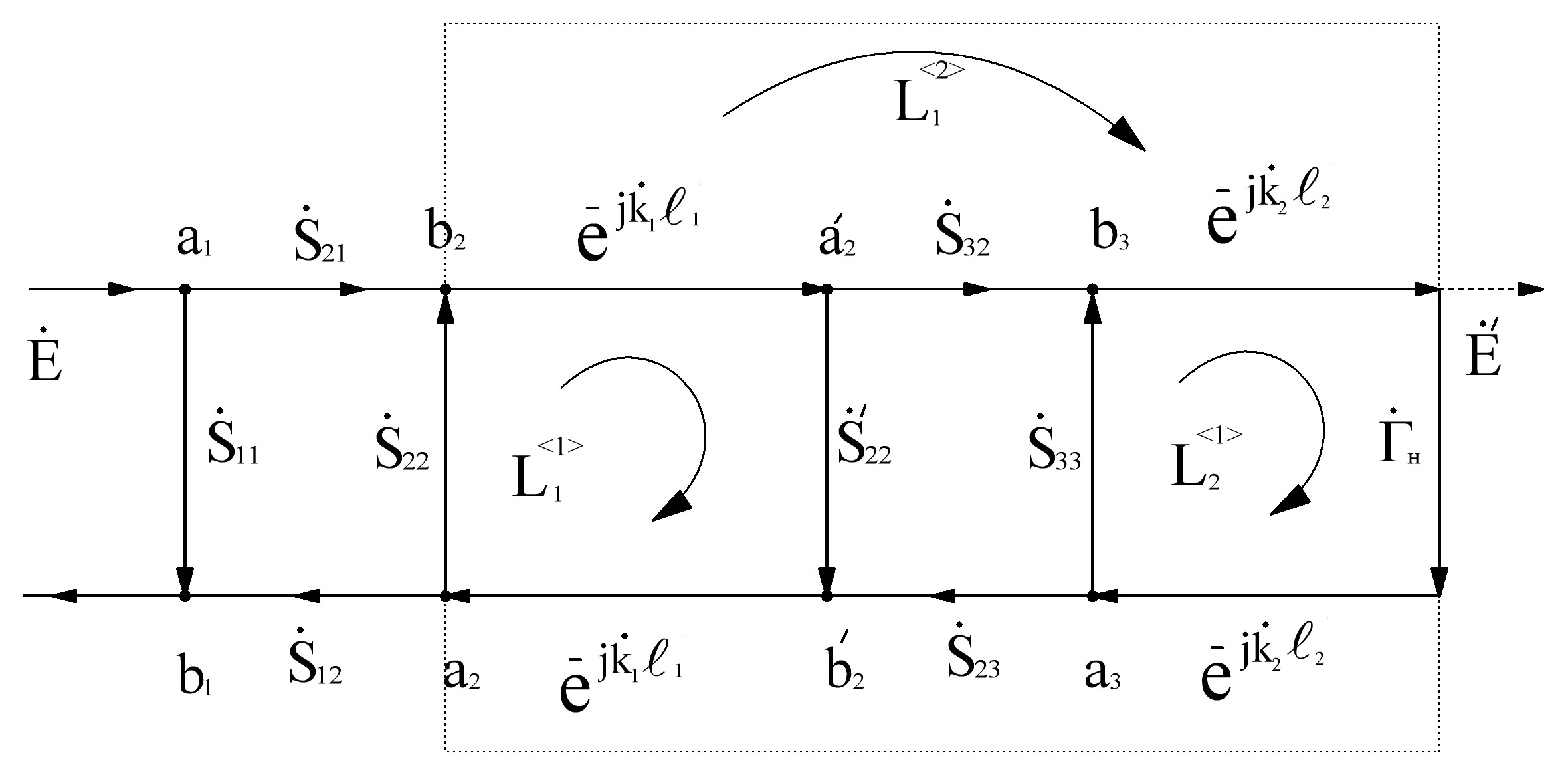
Рис.3.3 Граф структурной схемы

Граф сформирован в соответствии с теорией, которая была приведена выше. Где, S- Параметры рассеяния(коэффициенты отражения и передачи), a_i ,b_i зажимы четырехполюсника, - коэффициент отражения от воды, , комплексная амплитуда падающей и прошедшей среду волны соответственно. Для каждого четырехполюсника можно составить матрицу рассеяния.

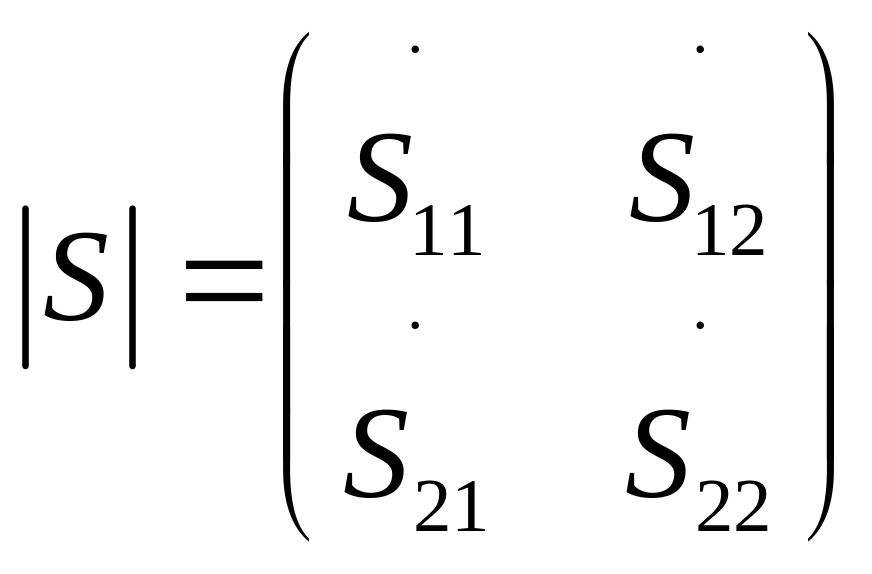
Матрица рассеяния для первого четырехполюсника.

Аналогично можно составить матрицу и для 2-го четырехполюсника, и для общего каскадного соединения в целом, но нам нет необходимости делать это.

4. Расчет коэффициента отражения земных радиоволн

Рассчитывать полный коэффициент отражение удобно по правилу не касающихся контуров.

Для этого проделаем два последовательных действия:

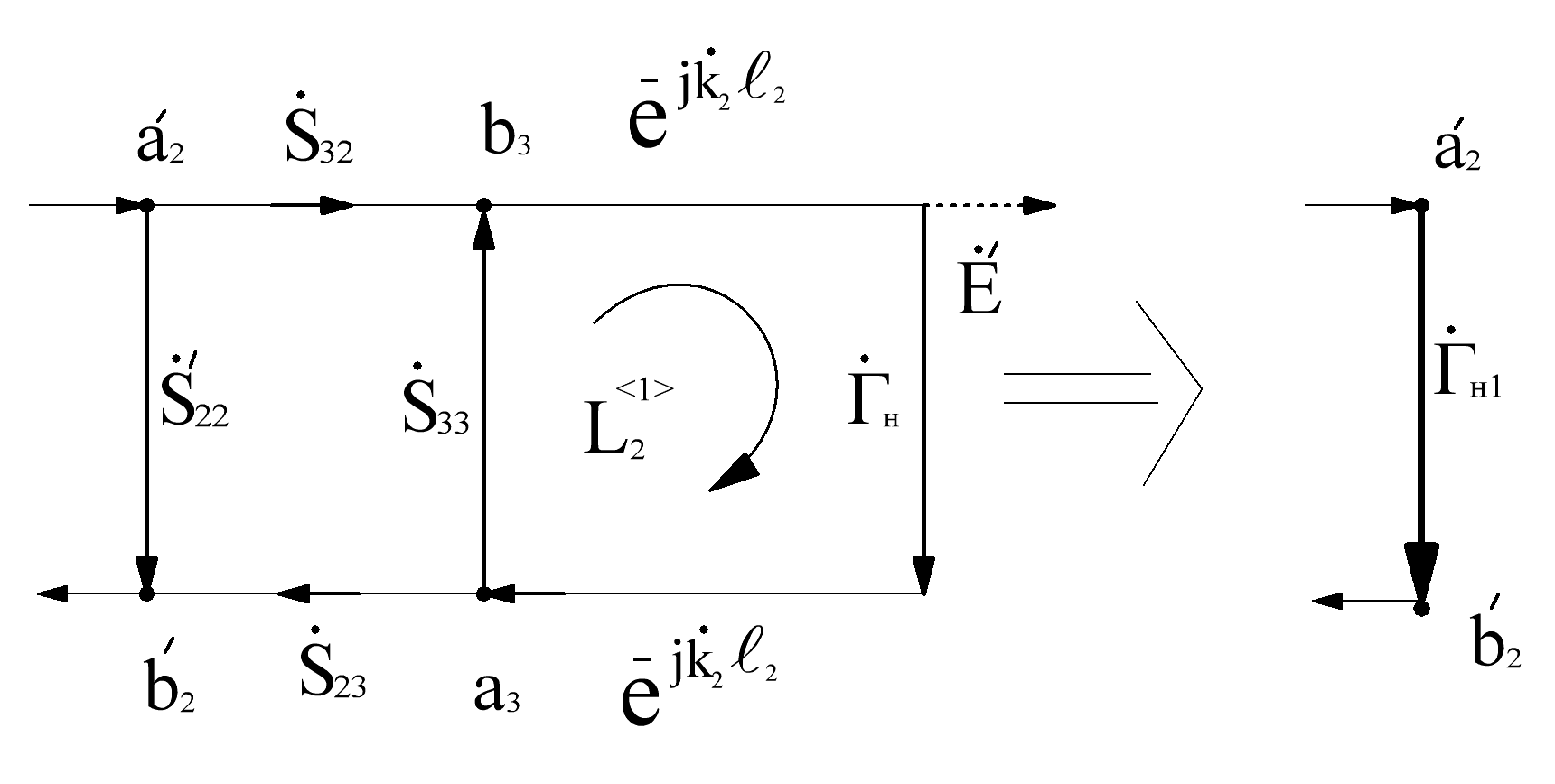
Рис. 4.1. Эквивалентное преобразование графа по коэффициенту отражения

По правилу не касающихся контуров пересчитаем часть графа изображенного на рис.4.1. в эквивалентную нагрузку с Г_Н1.

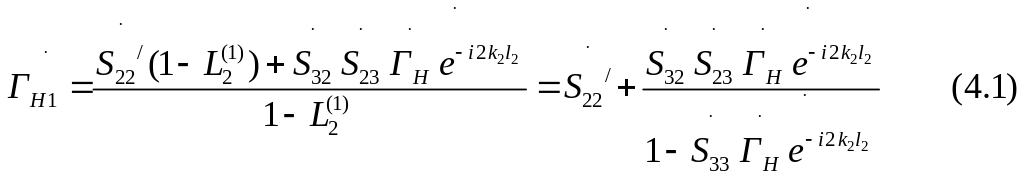
Далее выполним такое же преобразование по правило не касающихся контуров ( в качестве нагрузки теперь выступает новая нагрузка с коэффициентом отражения - ).

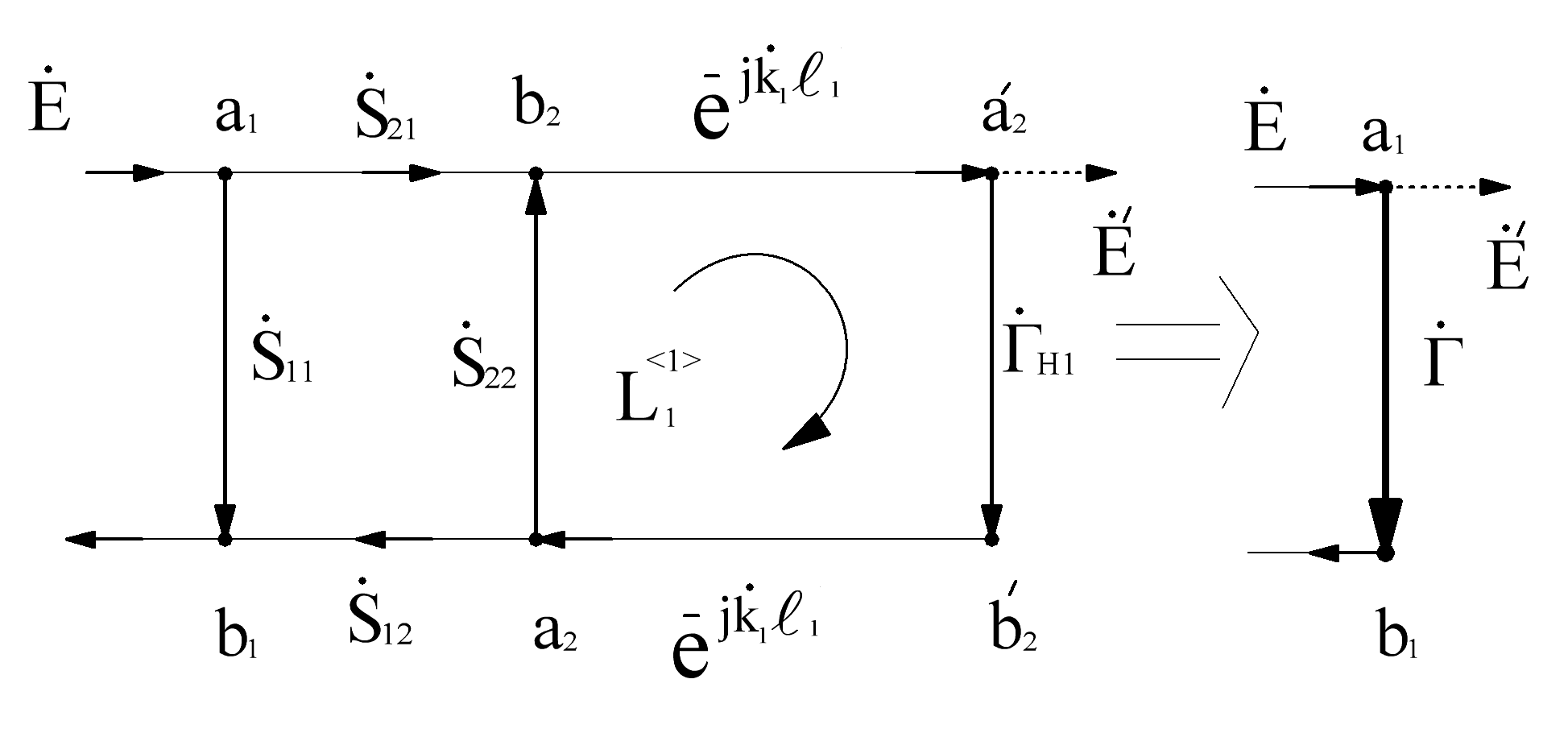
Рис. 4.2. Эквивалентное преобразование графа по коэффициенту отражения

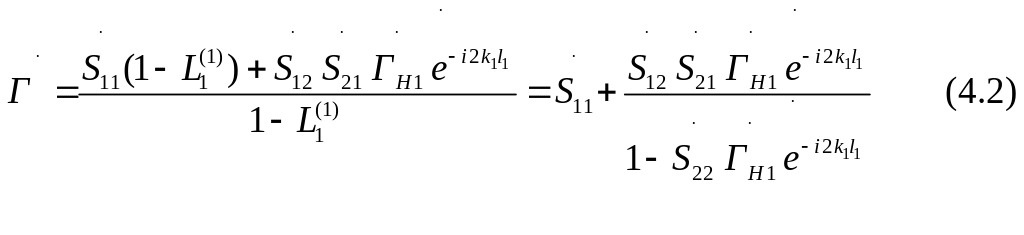
Теперь необходимо рассчитать парциальные коэффициенты отражения и прохождения .

Известно, что в соответствии с граничными условиями имеют место следующие выражения:

(4.3)

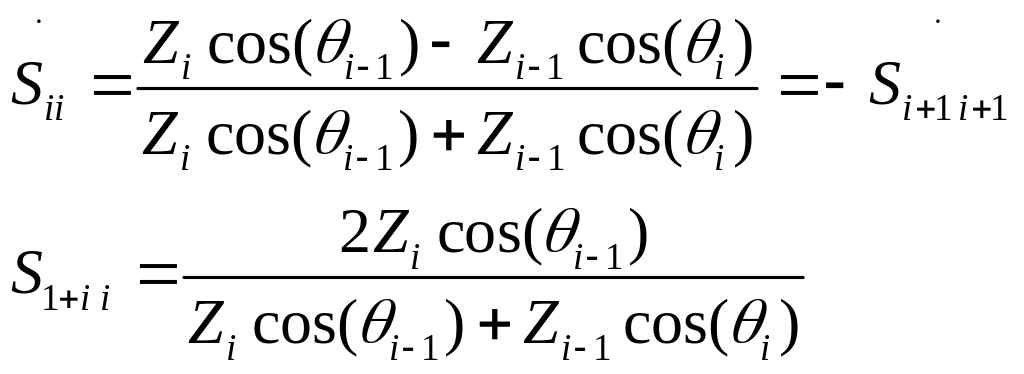(4.4)

Выражения 4.3 и 4.4 справедливы для волн, падающих в направлении распространения:

(4.5)

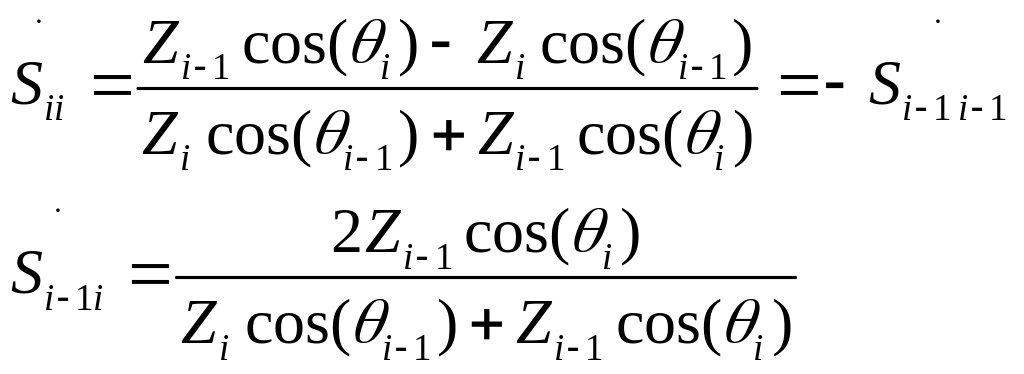. (4.6)

Выражения 3.5 и 3.6 справедливы для волн. Падающих против направления распространения ( отраженных). i>0 i<=4, т.к. для воды i=3, а для воздуха i=0.

- волновое сопротивление i-ой среды.

Для нагрузки можно записать .

Для исключения второстепенных углов и волновых сопротивлений, воспользуемся З. Снеллиуса, и связью волнового сопротивления со средой распространения:

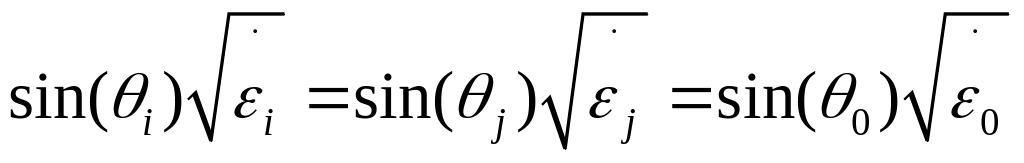(4.7)

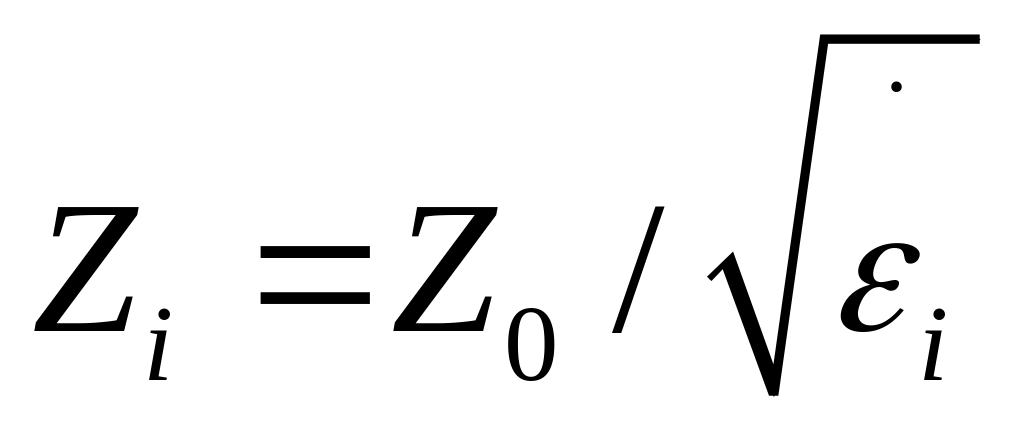(4.8),

Где .

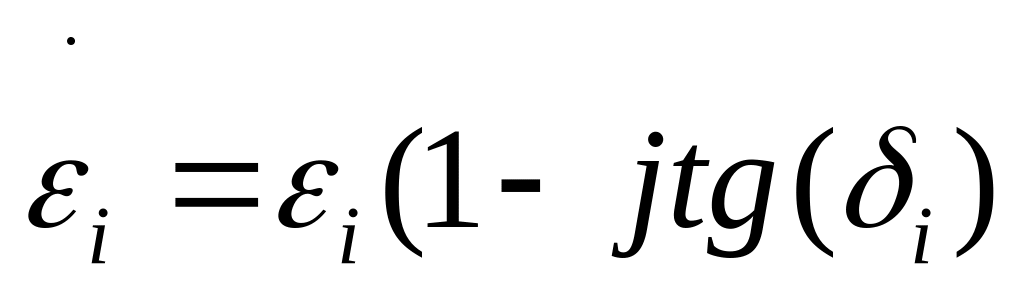Подставляя формулы 4.7 и 4.8 в формулы 4.2-4.6 получим формулы через угол падения и параметры среды:

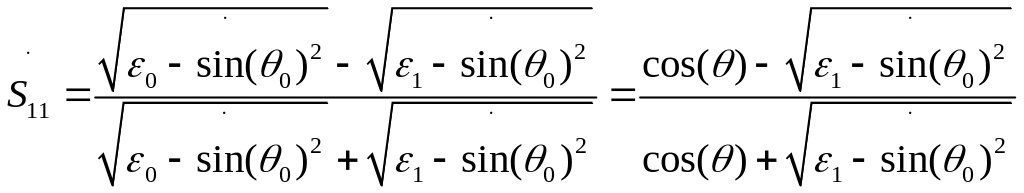(4.9)

(4.10)

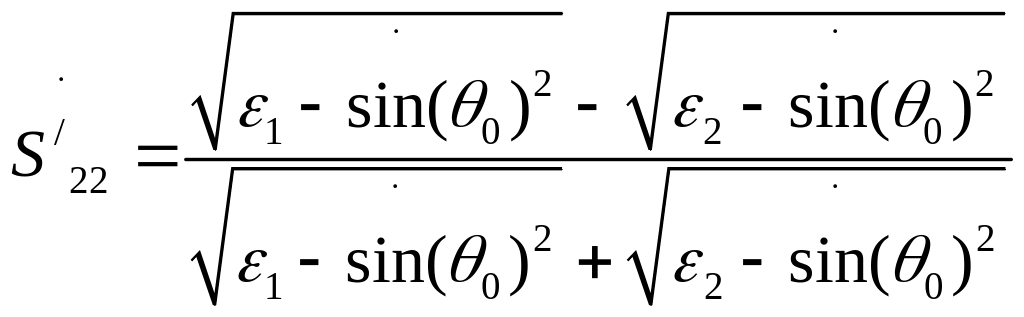(4.11)

(4.12)

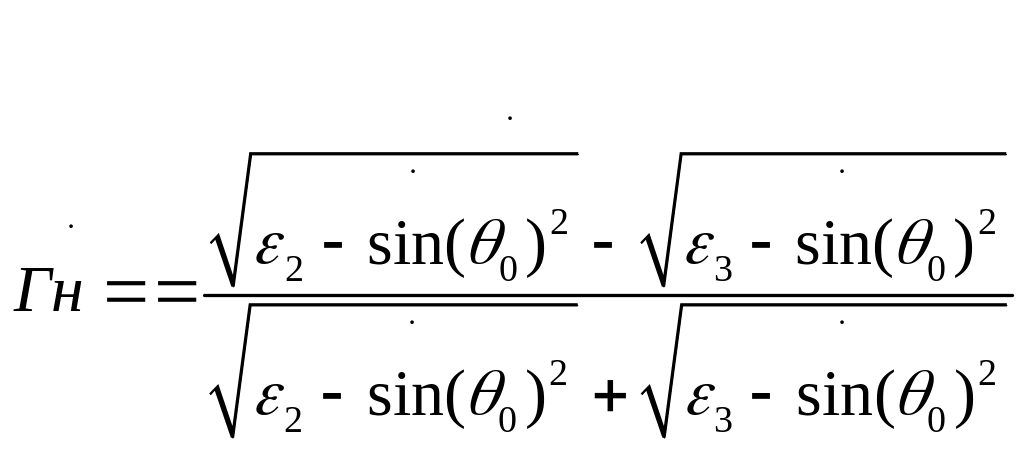(4.13)

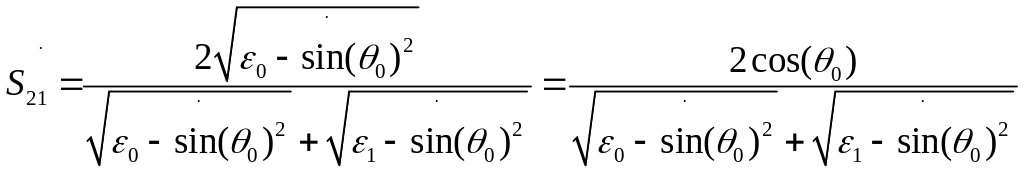(4.14)

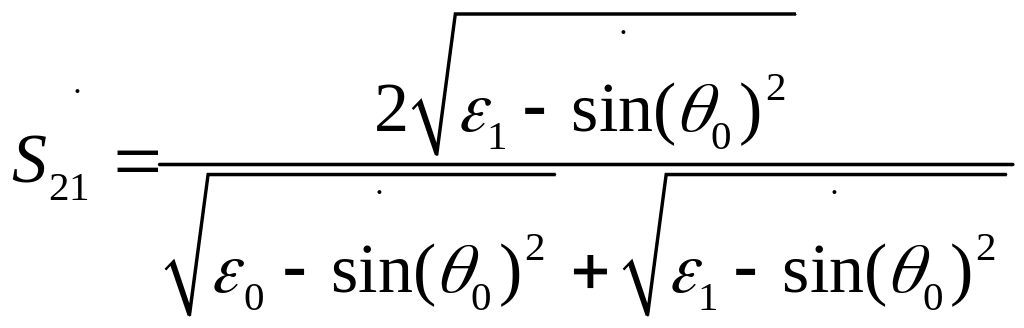(4.15)

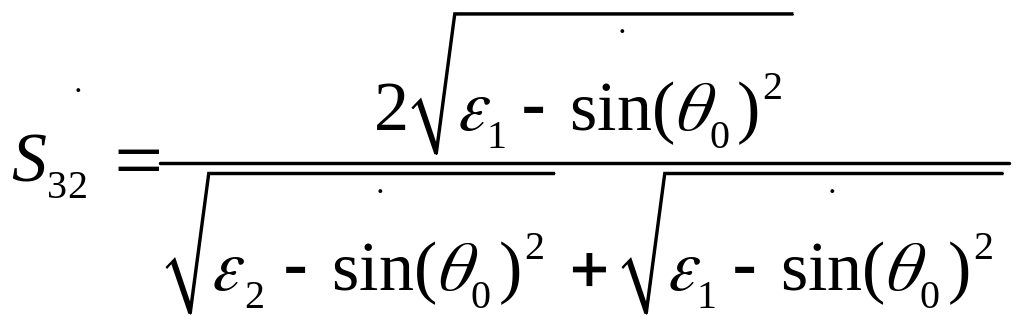(4.16)

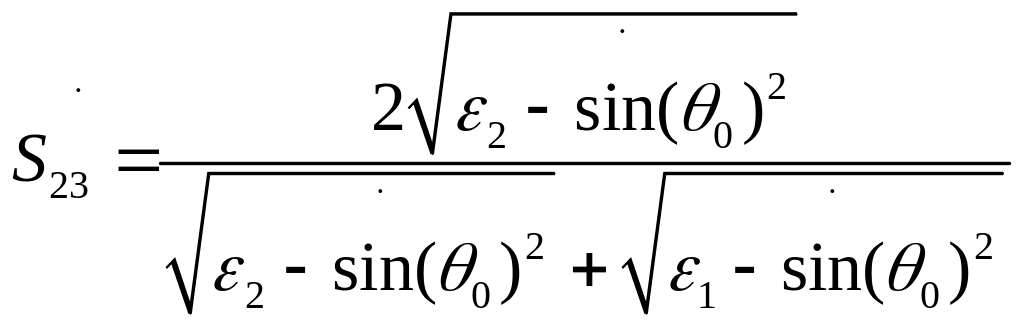. (4.17)

Длина физического пути радиоволны в среде определяется по следующим формулам:

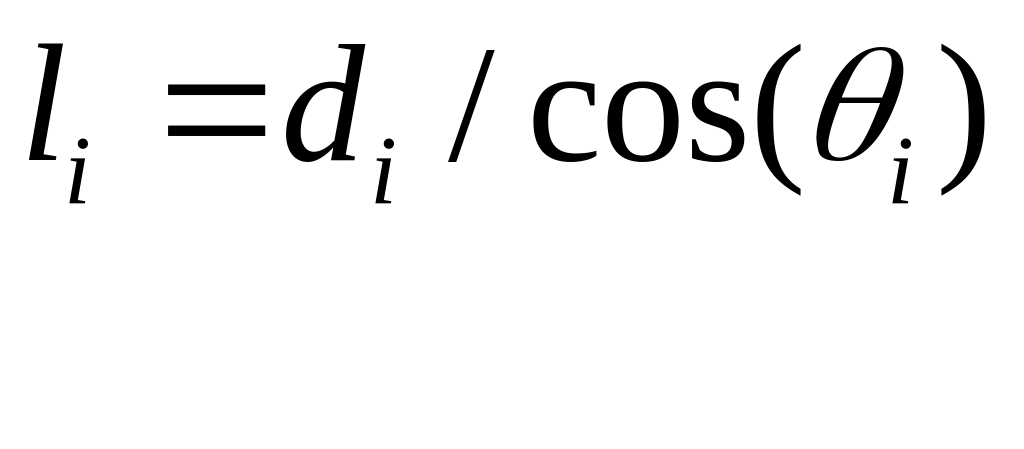(4.18)

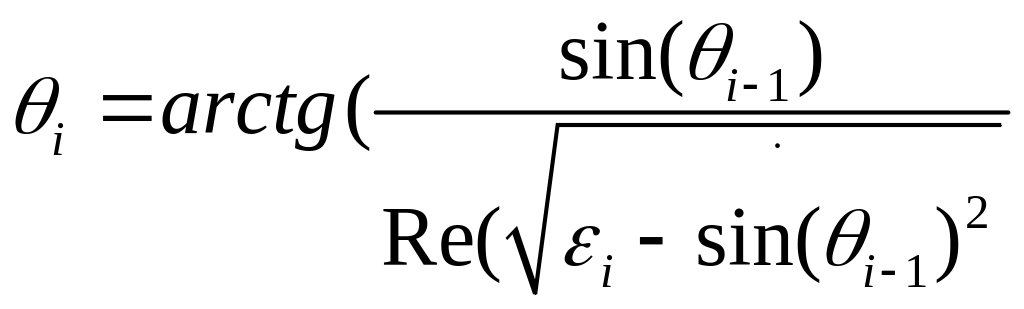(4.19)

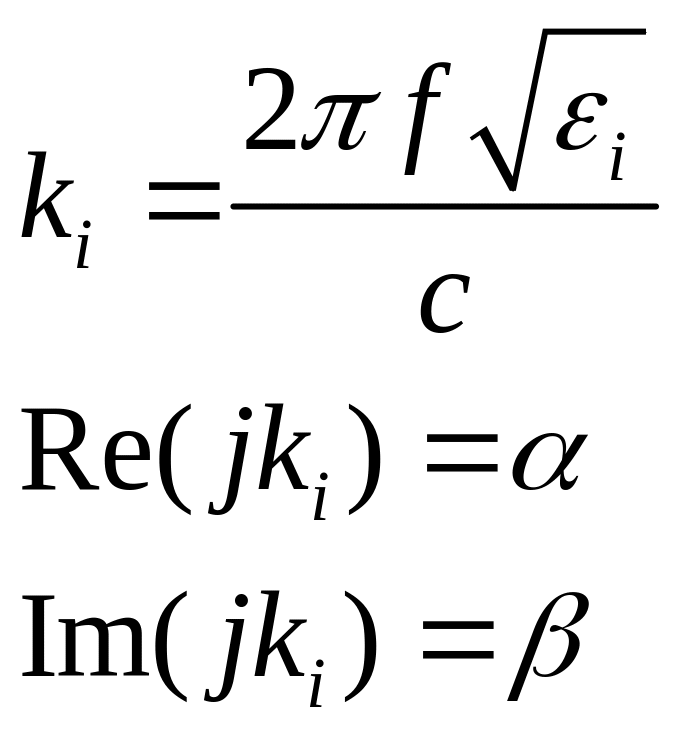. (4.20)

Приведем характеристики слоев, необходимые для расчета коэффициента отражения.

Следует отметить, что характеристики слоев слабо зависят от частоты, поэтому в интервале 1-10 Ггц, будем считать их постоянными.

Подставляю формулы 4.9-4.20 в формулы 4.1 и 4.2 , можем рассчитать полный коэффициент отражения при различных углах падения.

В общем случае полный коэффициент отражения комплексное число.

Поэтому на рис. 4.3 приведена зависимость модуля коэффициента ослабления от угла падения на границу воздух - холодный лед.

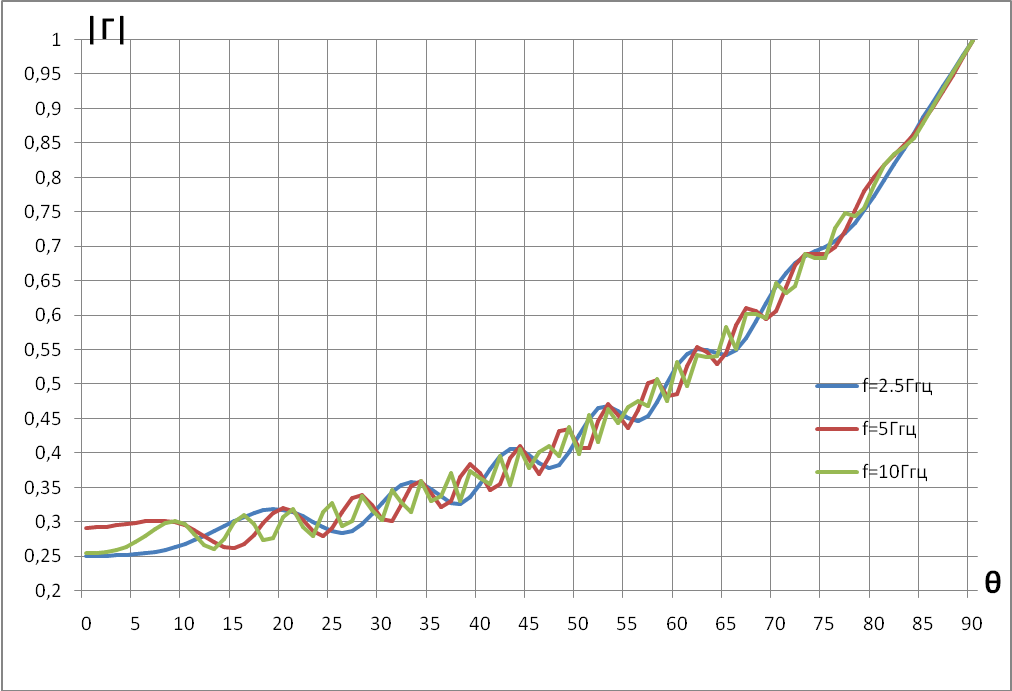
Рис. 4.3. Зависимость модуля коэффициента отражения от угла падения земной радиоволны.