V2: Виды напряженного состояния
I: K=С
S: Напряженное состояние в точке D имеет вид
-:
+:
-:
-:
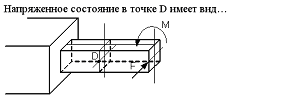
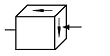
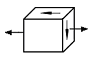
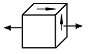
I: K=В
S: Вид напряженного состояния в точке С …
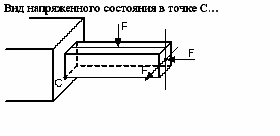
+: пространственное
-: линейное
-: точечное
-: плоское
I: K=В
S: Напряженное состояние, возникающее в точке С, имеет вид…
-:
-:
-:
+:
I: K=В
S: Вид (тип) напряженного состояния в окрестности какой-либо точки деформированного тела подразделяется на …
+: объёмное, плоское и линейное
-: косой изгиб, растяжение с изгибом, кручение с изгибом
-: растяжение, сжатие, изгиб
-: растяжение, сжатие, сдвиг
I: K=A
S: На одной грани элемента действуют нормальные напряжения. Такое напряженное состояние называется…
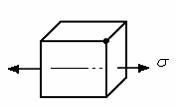
-: объемным (трехосным)
-: чистым сдвигом
+: линейным (одноосным)
-: плоским (двухосным)
I: K=A
S: Если на двух взаимно-перпендикулярных гранях элемента действуют только касательные напряжения, то такое напряженное состояние называется…
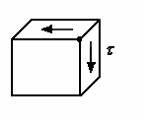
-: линейным (растяжение)
-: линейным (сжатие)
+: плоским (чистый сдвиг)
-: плоским (двухосное растяжение)
I: K=A
S: Тип (вид) напряженного состояния в окрестности точки К…
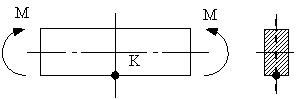
-: плоское (чистый сдвиг)
-: плоское (двухосное растяжение)
-: линейное (сжатие)
+: линейное (растяжение)
I: K=A
S: Вид (тип) напряженного состояния в окрестности точки К…
+: «нулевое» – напряжения отсутствуют
-: линейное – растяжение
-: линейное – сжатие
-: плоское – чистый сдвиг
I: K=В
S: В окрестности точки К консольной балки напряженное состояние…
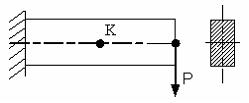
+: плоское (чистый сдвиг)
-: линейное (одноосное сжатие)
-: линейное (одноосное растяжение)
-: «нулевое» – напряжения отсутствуют
I: K=В
S: Два напряженных состояния называются равноопасными, если они имеют…
-: одинаковые знаки нормальных напряжений
-: одинаковые знаки наибольших касательных напряжений
-: одинаковые знаки главных напряжений
+: одинаковые коэффициенты запаса
I: K=A
S: Совокупность напряжений, действующих по всем площадкам, называется …
-: состоянием напряжения
+: напряженным состоянием
-: полным напряжением
-: трехосным напряжением
I: K=A
S: Напряженное состояние, при котором два главных напряжения равны нулю, называется …
-: пространственное
+: линейное
-: точечное
-: плоское
I: K=A
S: Напряженное состояние, при котором одно из главных напряжений равно нулю …
-: пространственное
-: линейное
-: точечное
+: плоское
I: K=A
S: Напряженное состояние изображенное на рисунке
-: пространственное
+: линейное
-: точечное
-: плоское
I: K=A
S: Напряженное состояние изображенное на рисунке
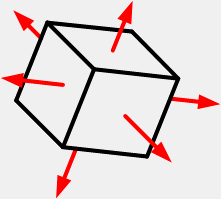
+: пространственное
-: линейное
-: точечное
-: плоское
I: K=A
S: Напряженное состояние изображенное на рисунке
-: пространственное
-: линейное
-: точечное
+: плоское
I: K=В
S: Напряженное состояние изображенное на рисунке
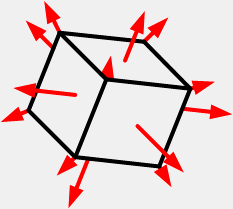
-: пространственное
-: линейное
+: ни одно из перечисленных
-: плоское
I: K=A
S: Напряженное состояние, при котором все три главных напряжения отличны от нуля …
+: пространственное напряженное состояние
-: линейное напряженное состояние
-: точечное напряженное состояние
-: плоское напряженное состояние
I: K=В
S: При линейном напряженном состоянии Закон Гука выражается зависимостью…
-:
+:
-:
-:
I: K=A
S: Пространственное напряженное состояние …
-:
+:
-:
-:
I: K=A
S: Линейное напряженное состояние
+:
-:
-:
-:
I: K=A
S: Плоское напряженное состояние…
-:
-:
+:
-:
I: K=С
S:
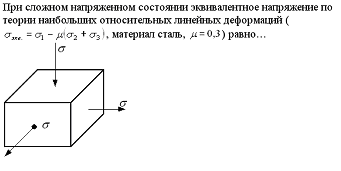
При сложном напряженном состоянии
эквивалентное напряжение по теории
наибольших относительных линейных
деформаций (
,
материал сталь, =0,3)
равно …
+:
-: 1,6
-: 0
-: 1,3