Розділ 3. Характеристика і вимоги до геоінформаційного моделювання вулично-дорожніх мереж

Ключовими словами картографічного моделювання ВДМ в ГІС є " взаємодія" і "динаміка". Дослідники та й пересічні користувачі бажають, "натиснувши мишкою" на карті, одержати безпосередню та негайну реакцію системи з більш деталізованою інформацією про вибрані об'єкти ( земельні ділянки, пам’ятки історії, будівлі, інженерні комунікації, ВДМ, стан довкілля тощо) або, наприклад, одержати зображення та опис найкоротшого шляху між заданими пунктами, а можливо, і "проїхати" по ньому з використанням комп'ютерних мультимедійних засобів та анімації. Остання, до речі, надає такі можливості просторово-часового моделювання, яких традиційна картографія ніколи не мала. Геозображення формуються з динамічною зміною масштабу, а їх зміст залежить переважно від повноти бази геопросторових даних, потреб і запитів користувачів, а не від картографічних правил і бачення картографів.

В ГІС переважає парадигма винятковості геопросторових даних, наслідком якої є різноманіття підходів та форматів від різних виробників інструментальних ГІС поряд з високим рівнем уніфікації представлення і обробки фактографічних даних в універсальних системах управління базами даних (СУБД) на рівні стандартної мови SQL та уніфікованих механізмів і засобів доступу до даних. В геоінформаційних системах третього покоління спостерігається повне інтегрування ГІС з універсальними СУБД, а також їх вихід у глобальний інформаційний простір через Internet.

3.1. Структура геометричної моделі

Просторове розташування, форма та розміри комунікаційних об'єктів визначається різнотипними даними, що складають геометричну інформацію. Відображаючи просторові властивості топографічного об'єкту, ця інформація забезпечує просторову цілісність моделі місцевості. Особливістю геометричних даних є те, що складна форма об'єктів моделюється за допомогою ортогональних проекцій цих об'єктів на земну поверхню. Проекції об'єктів створюють систему просторових поверхонь з граничними лініями - контурами.

Геометрична інформація складається з двох видів даних: метричної та синтаксичної інформації.

Метрична інформація (Мі) є множина даних про просторове розташування точок топографічного об'єкту на земній поверхні. До цієї інформації належать координати та висоти точок інженерних комунікацій, отриманих у результаті геодезичних, фотограмметричних чи картографічних вимірювань. Метрична модель топографічного об'єкту визначається вектором Мі = ( х, у, Н),

де х, у, Н - просторові координати точки інженерних комунікацій. Метричній моделі топографічного об'єкту відповідає поняття POINT в сучасних геоінформаційних системах.

Синтаксична інформація характеризує геометричну форму контурів та рельєфу місцевості і визначає послідовність точок, які складають топографічний об'єкт, та спосіб їх з'єднання: пряма лінія, дуга, сплайн тощо.

Факторами, що визначають вибір типу моделі об'єкту за принципом просторової локалізації, є його розміри - довжина контуру l та площа основи р, які порівнюються з заданими l₃, p₃. За типом просторової локалізації всі топографічні об'єкти поділяються на точкові, лінійні та площинні об'єкти.

Точкова модель – модель m_т, для якої m_т ( l_т < l₃ , p_т < p₃), що відображає положення об'єкту точкою прив'язки до центру ваги.

Лінійна модель – модель m_л, для якої m_л ( l_л > l₃ , ( p_л / l_л) < ( p₃/ l₃)), що відображає положення об'єкту лінією прив'язки контуру.

Площинна модель – модель m_n, для якої m_п ( l_Т > l₃, ( p_л / l_Л) < ( p₃/ l₃ ) , що відображає просторове положення об'єкту лінією його контуру.

Векторна нетопологічна геометрична модель передбачає створення лінійних та площинних топографічних об'єктів без урахування взаємозв'язків між ними.

Сучасну векторно-топологічну геометричну модель в геоінформаційних системах ВДМ представимо у формі ланцюгово-вузлової структури. Основні поняття вузлово-ланцюгової структури складаються з моделей:

• сегмент;

• ламана;

• дуга;

• вершина дуги;

• вузли дуги;

• полігон.

Сегмент – відрізок на площині чи іншій поверхні з кінцями, М_п та М_к, позначених як С = { М_п, М_к }, при цьому початкова та кінцева точки не співпадають.

Ламана – упорядкована сукупність одного чи кількох сегментів Л = [M_l, M₂] [М₂, М_З,] [М_З, M₄] ... [М_і , М_і+1] за визначенням початок наступного сегменту співпадає з кінцем попереднього при цьому початкова та кінцева точки не співпадають. Ламана може мати взаємно пересіченні сегменти .

Дуга - ламана, Л = [М₁, М₂] [М₂, М_З] [М_З, М₄] ... [М_і, М_і+1], що не пересікається сама з собою, з такою додатковою умовою: будь-які пари сегментів не мають спільних точок. Поняттю дуга в термінах сучасних геоінформаційних систем відповідають поняття: ARC, LINE, FACE / EDGE, CHAIN.

Вузол дуги – це початкова M_l або кінцева М_п точка дуги.

Полігон – це множина дуг, у яких вузол початку наступної дуги співпадає з вузлом кінця попередньої дуги, при цьому початковий вузол першої дуги та кінцевий вузол останньої дуги співпадають. Поняттю полігон в сучасних геоінформаційних системах відповідають поняття POLYGON, AREA, REGION.

Загальну схему ВДМ представлено на наступній схемі (рис. 12).

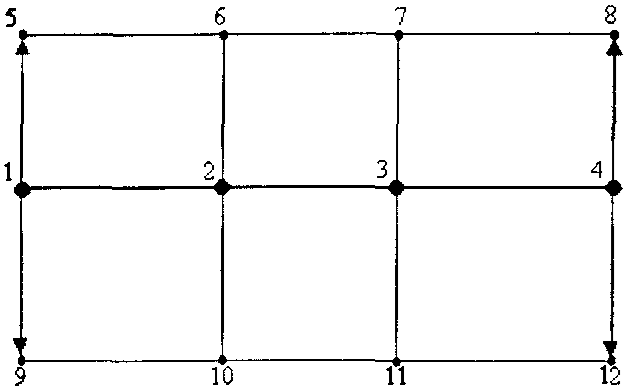
Рис.12. Загальна схема ВДМ

Згідно вищенаведеного, з рис.12 випливає наступне:

• 1,2,3,4 - вузлові точки;

• 5,6,7,8,9,10,11,12 – точки ВДМ (перехрестя);

• 1-2, 2-3, 3-4 і т.д. – дуги.

На основі теорії графів складаємо рівняння вузлів, дуг та полігонів.

Рівняння вузлів:

N₁ = {X₁, Y₁, Н₁}; N₂ = {Х₂, Y₂, Н₂};

N₃ = {Х_З, Y₃, Н_З}; N₄ = {Х₄, Y₄, Н₄} ;

………………………………………..

N₁₁ = {X₁₁, Y₁₁, H₁₁}; N₁₂ = {Х₁₂, Y₁₂, Н₁₂}.

Рівняння дуг:

L₁ = {N₁ U N₂} ; L₂ = {N₂ U N₃};

L₃ = {N₃ U N₄} ; L₄ = {N₁ U N₅};

…………………………………….

L₁₆ = {N₁₀UN₁₁} ; L₁₇ = {N₁₁UN₁₂} .

Рівняння полігонів:

P₁ = {L₁ U L₅ U L₈ U L₄};

P₂ = {L₂ U L₆ U L₉ U L₅};

……………………………………….

P₆ = {L₁₇UL₁₄UL₃UL₃}.