4.2. Теория отражательного клистрона

Основные закономерности отражательного клистрона можно выявить при качественном рассмотрении процессов возникновения автоколебаний. Для этих целей достаточно простой теории с рядом упрощающих предположений:

- пренебрегается действием расталкивающих сил объемного заряда в потоке электронов;

- амплитуда переменного напряжения на сетках резонатора мала по сравнению с ускоряющим напряжением;

- резонатор клистрона заменяется высокодобротным параллельным колебательным контуром;

- рассматривается одномерная задача без учёта краевых эффектов, разброса скоростей электронов и т.д.

4.2.1. Модуляция и группировка электронного потока

Под действием ускоряющего напряжения резонатора электроны приобретают кинетическую энергию

,

где , - заряд и масса электрона. Скорость электронов в плоскости первой сетки

В зазоре резонатора действует переменное напряжение . Движение электронов в зазоре описывается уравнением

, (1)

где - расстояние между сетками.

Интегрируя уравнение (1) при начальных условиях , , найдем скорость электронов в момент вылета из резонатора

. (2)

Так как время пролета электронами зазора резонатора сравнимо с периодом СВЧ-колебаний, то отсчитывается в относительных единицах ( период колебаний), измеряется в радианах и в дальнейшем называется пролетным углом

.

Если скорость электрона в зазоре постоянна, то .

Выражение (2) преобразуется к виду

(3)

При малых углах пролета (при ). После введения обозначений:

- коэффициент использования напряжения;

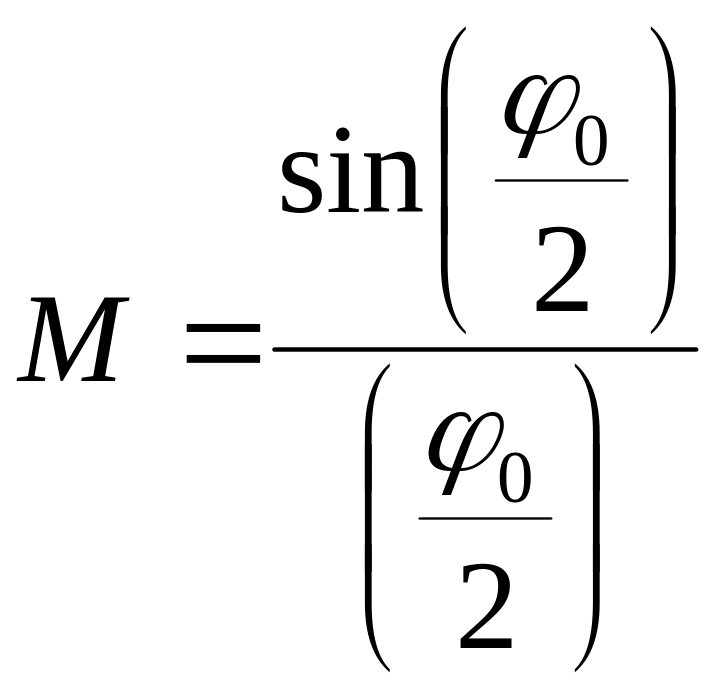- коэффициент модуляции скорости,

окончательно перепишем формулу (3):

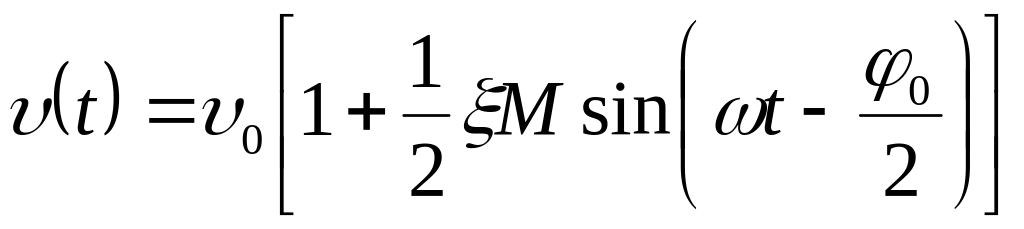(4)

Скорость электронного потока (4) на выходе из резонатора помимо постоянной составляющей имеет переменную гармоническую составляющую. Коэффициент модуляции зависит от управляющего напряжения , и угла пролета .

В пространстве отражателя электронный поток движется в однородном тормозящем поле . Из-за того, что электроны, вылетевшие из резонатора в различное время, имеют отличающиеся скорости (4), они проходят пространство отражателя за разное время. Электроны, вылетевшие из межсеточного пространства позднее, но имеющие большую скорость, догоняют более "медленные" электроны, что приводит к перераспределению заряда в потоке. Время движения электронов в пространстве отражателя (где - время вылета из резонатора, - время возвращения в резонатор) находится из закона равнозамедленного движения.

. (5)

Для угла пролета в пространстве отражателя ( ) получим 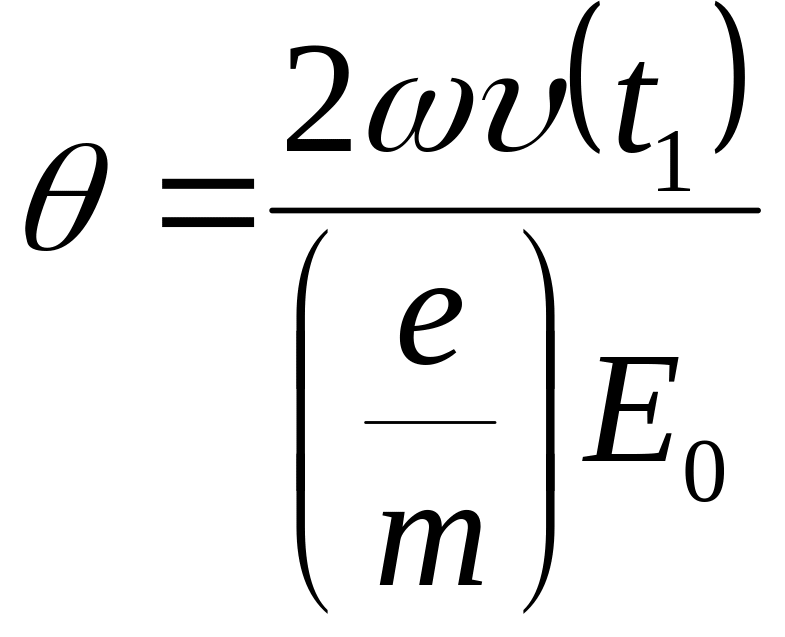. (5)

Учитывая (4) получим закон модуляции угла пролета:

; (6)

где 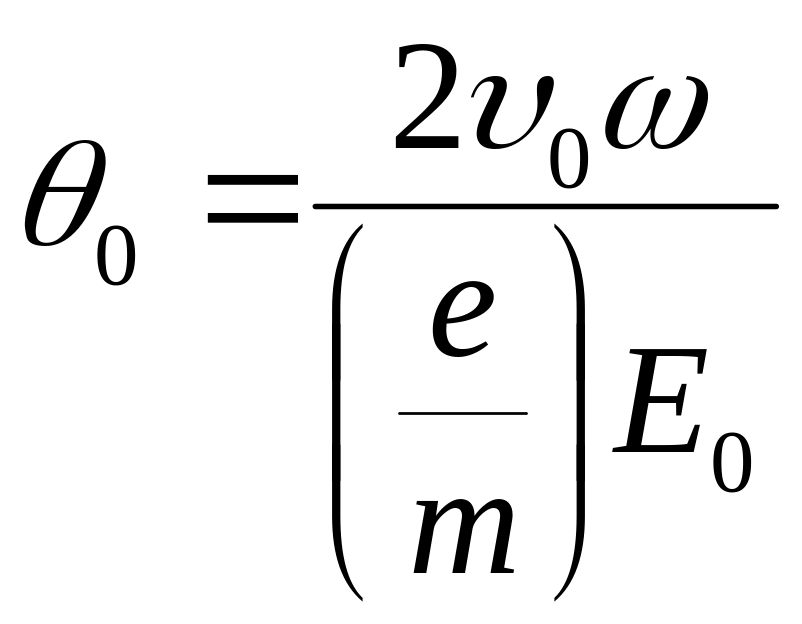- средний угол пролета; - параметр группировки.

Выражение (6) определяет фазу возвращения электронов в резонатор в зависимости от фазы его вылета. При каждой фазе вылета соответствует своя фаза возвращения, т.е. группировки нет. При электроны, вылетевшие в моменты ; ; , возвращаются в резонатор в одно и то же время. Таким образом, параметр определяет степень сгруппированности потока, а значит и амплитуду переменной компоненты конвекционного тока, возвращающегося в резонатор. Параметр группировки зависит от амплитуды переменного напряжения в резонаторе и среднего угла пролета в пространстве группировки . С ростом увеличивается переменная составляющая скорости электронов в потоке, а возрастание означает увеличение пути потока в пространстве отражателя, что ведет к увеличению плотности заряда в сгустке. Используя закон сохранения заряда можно найти переменный ток через резонатор:

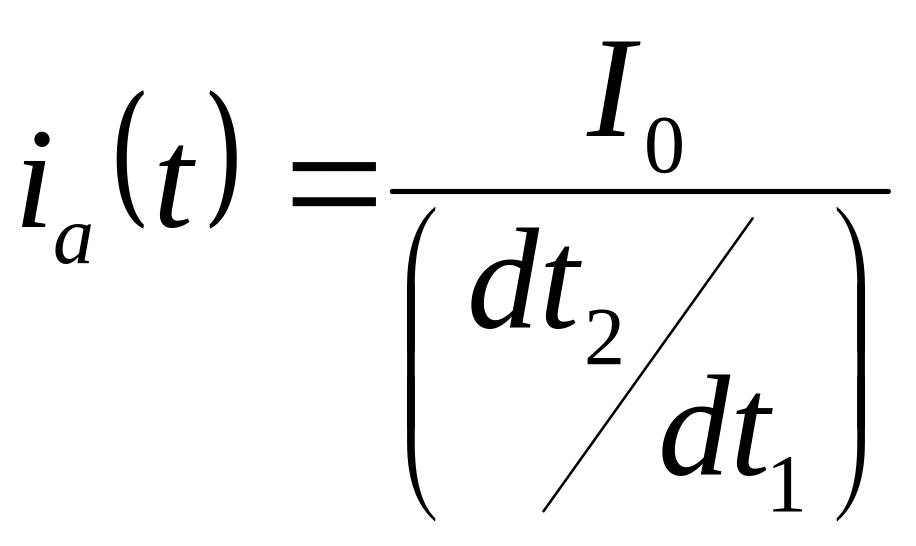
Производная находится из выражения (6). Следовательно,

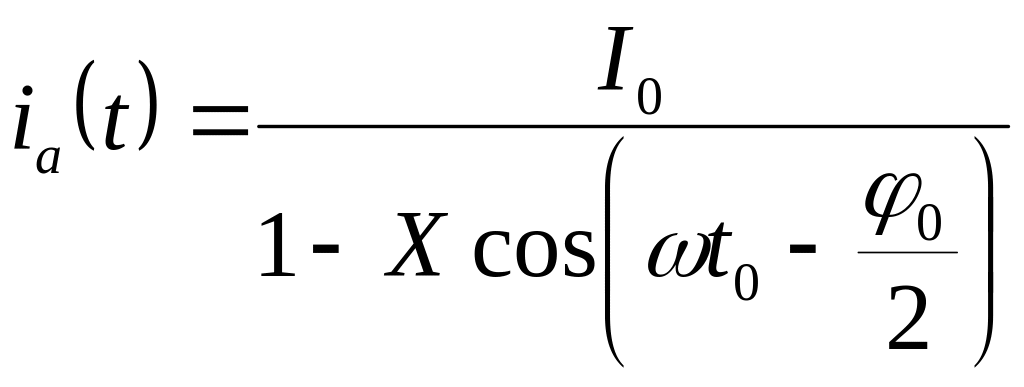(7)

при

.

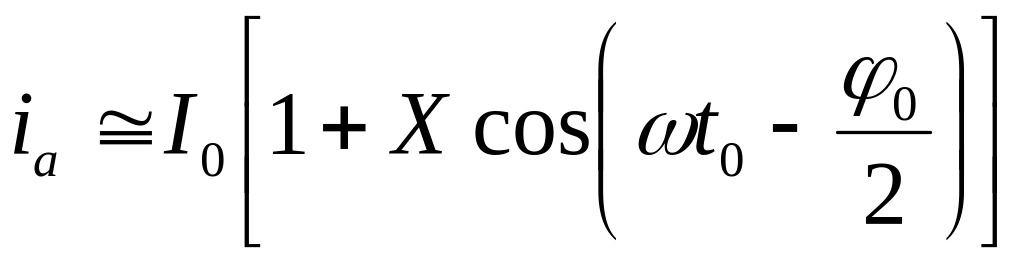
Рис. 6. График прибытия электронов в резонатор

Рис. 7. Группировка электронного потока, модулированного по скорости

Зависимость i_a от времени показана на рис 7. В начале движения потока в пространстве группировки периферийные электроны приближаются к электронам, летящим в центре сгустка, и плотность заряда постепенно возрастает (рис. 7 а, в). При большом времени движения периферийные электроны не только догоняют центральные, но и перегоняют их, сгусток деформируется, и максимум его раздваивается. Это свидетельствует о нелинейности процесса группировки. При больших ток резко несинусоидален. В силу высокой добротности резонатора клистрона практически значима только первая гармоника, частота которой равна собственной частоте резонатора. Гармонический анализ тока (7) дает следующее выражение для первой гармоники:

, (8)

где - постоянная составляющая конвекционного тока; - функция Бесселя первого рода.

Из выражения (8) следует нелинейная амплитудная характеристика клистрона. С ростом амплитуда первой гармонии увеличивается, достигает максимума и затем уменьшается. Это приводит к установлению в клистроне стационарного устойчивого режима генерации.