3.1. Резонатор с сосредоточенными параметрами

Простой СВЧ–резонатор с сосредоточенными параметрами показан схематически на рис.1. Резонатор состоит из одновитковой катушки индуктивности и двух зазоров, представляющих собой емкость. Применяются также резонаторы с одним и четырьмя зазорами.

Емкостные и индуктивные элементы разделены в пространстве и в хорошем приближении СВЧ магнитное поле сосредоточено внутри цилиндра, а электрическое поле в щелях.

Классическое выражение для индуктивности и емкости при наличии щелей имеет вид (обозначения на рис.1.):

; (1)

и резонансная частота

(2)

Р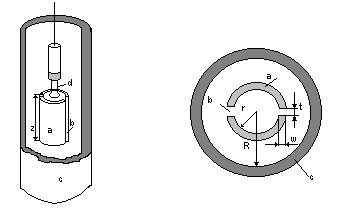 ис.1. Индуктивно – щелевой резонатор. Основные элементы: a – индуктивный элемент; b – щель (емкость); c – экран; d – индуктивная связь с коаксиальной линией. Z = 10 (длина резонатора); r = 2.5 (радиус резонатора); R = 5 (радиус экрана); t = 0.2 , w = 0.4 (размеры щели, образующей емкость). f₀≈9 ГГц.

Это уравнение приближенное. Когда размеры резонатора приближаются к /4, резонатор может излучать, что приводит к уменьшению Q. Излучение может быть ограничено с помощью цилиндрического экрана, радиус которого должен быть меньше основного типа колебаний, возбуждаемых в цилиндрическом волноводе. Наличие экрана и краевых полей щели изменяет частоту, и она уже не определяется уравнением (2).

Полуэмпирическое уравнение

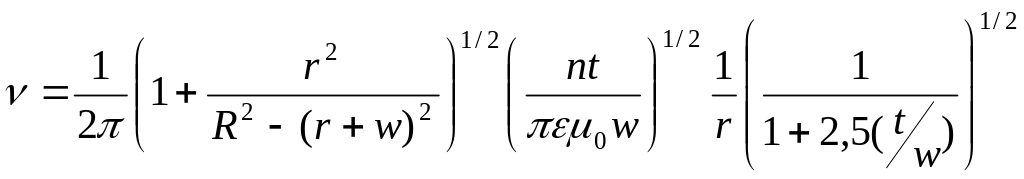(3)

является удовлетворительным при вычислении резонансной частоты в интервале 110 ГГц. Первый член в скобках введен для учета влияния экрана. Последний член описывает влияние краевых полей щели. Добротность резонатора может быть вычислена без учета потерь по формуле

, (4)

где  - глубина скин-слоя.

С учетом влияния экрана

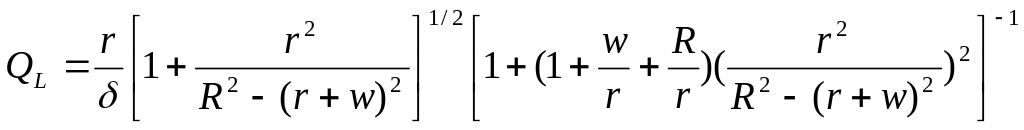(5)

К этому должны быть добавлены потери проводимости конденсатора, образованного щелью

, (6)

где t, w в метрах,  в герцах,  для вакуума 8. 85  10 ^{– 12} . Окончательно

(7)

Амплитуда радиочастотного магнитного поля в соответствующем резонаторе изменяется так

, (8)

или приблизительно

, (9)

где Р₀ – поступающая в резонатор мощность.

3.2. Объемный резонатор (прямоугольный)

В прямоугольных резонаторах могут существовать как моды ТЕ _mnp , так и моды ТМ _mnp. Индексы m, n, p суть числа стоячих полуволн соответственно в направлениях x, y, z (рис.2.). Эти моды получаются из волн типа ТЕ _mn и ТМ _mn в волноводе за счет того, что длина резонатора выбирается равной (2d)/_в. Размеры резонатора в направлениях x, y, z составляют соответственно a, b, d. Постоянная распространения

(10)

имеет компоненты

(11)

Резонансная частота 2₀ = ₀ определяется из уравнения

(12)

При вычислении добротности объемных резонаторов обычно используется энергетический подход, согласно которому добротность связывается с накопленной в системе энергией в режиме установившихся колебаний и с энергией, рассеиваемой системой за период собственных колебаний

, (13)

где W _нак – энергия, накопленная резонансной системой; (W _расс) _т – энергия, рассеиваемая в ней за период; Р_{расс. рез.} – мощность, рассеиваемая в резонаторе.

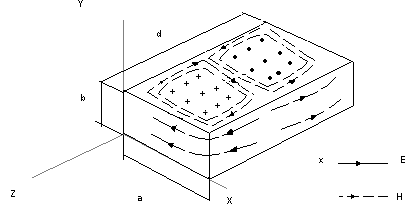
Рис.2. Структура электромагнитного поля в прямоугольном резонаторе с модой ТЕ ₁₀₂.

Р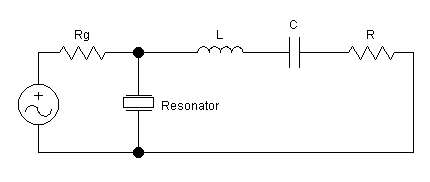 ис.3. Эквивалентная схема отражательного резонатора.

Накопленная энергия выражается через амплитуду напряженности магнитного поля Н в виде

(13)

а рассеиваемая в резонаторе за один период равна

(14)

где _ст – активная проводимость стенок,  - толщина скин-слоя, Н_t – тангенциальная составляющая высокочастотного магнитного поля у стенок резонатора.

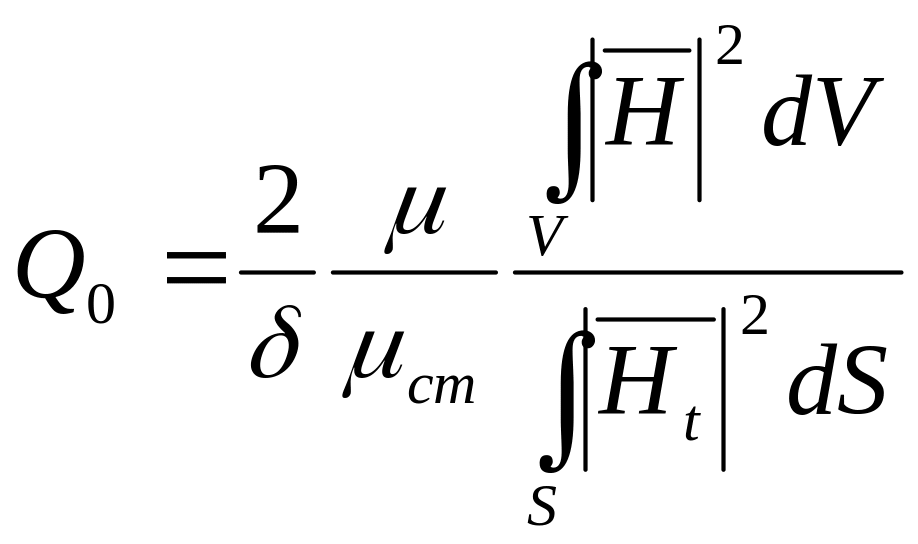(15)

Для качественной иллюстрации полученных уравнений предположим, что Н=Н_t=const.

Тогда

(16)

В случае моды ТЕ₁₀₂ для нагруженной добротности Q₀ имеем точное выражение:

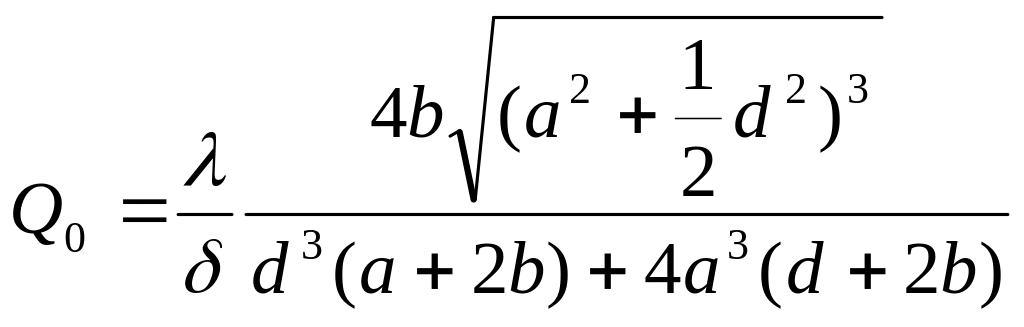(17)

А в случае моды ТЕ₁₀₁:

(18)

Рассматриваемое значение Q₀ (ненагруженная добротность) характеризует резонатор, без каких–либо элементов связи. Соединение с волноводом посредством диафрагмы или другого элемента связи вызывает понижение добротности Q. Понижение добротности характеризуется радиационной добротностью Q_r.

Отверстие связи иногда удобно представить в виде трансформатора с коэффициентом трансформации n. На рис.3. приведена эквивалентная схема отражательного резонатора. Для отражательного резонатора радиационная добротность имеет величину

,

где R_G – сумма характеристического сопротивления волновода и импеданса генератора. Ненагруженная добротность Q₀, включающая омические потери в стенках резонатора и диэлектрические потери в образце, равна

Отношение этих добротностей равно параметру связи :

(19)

Радиационная добротность характеризует потери, обусловленные мощностью, которая уходит из резонатора через отверстие связи, чтобы потом быть рассеянной в R₀. Общая, или ненагруженная, добротность определяется так:

(20)

Если резонатор идеально согласован с волноводом, то  = КСВН = 1 и при резонансе объемный резонатор замыкает линию передачи на ее характеристическое сопротивление Z₀. При сильной связи

и коэффициент стоячей волны по напряжению (КСВН) равен параметру связи

 = КCВН,

поскольку линия передачи замкнута на сопротивление, большее, чем ее характеристическое сопротивление Z₀. При слабой связи

,

Параметр связи характеризует эффективность процесса передачи мощности внешней нагрузке и последующего рассеяния в этой нагрузке энергии, накапливаемой в узлах связи резонатора.