2.2. Матрица рассеяния волноводного четырехполюсника
Четырехполюсник
СВЧ - устройство, имеющее два входа.
Напряжение электрического поля
отраженной и падающей на эти входы
нормированных волн есть соответственно
,
и
,
(см. рис.1).
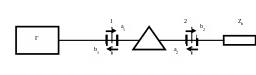
Рис. 1. Падающие и отраженные волны в четырехполюснике
Уравнения (2) для этого случая записываются так:
Если в многополюснике
отсутствуют потери, то сумма мощностей,
падающая на входы, равна сумме мощностей,
отраженной от них. Эта ситуация должна
иметь место при любых возможных
возбуждениях недиссипативного
многополюсника. Поэтому, если
четырехполюсник недиссипативный и
взаимный, то при согласованных входах
мощность из входа 1 без потерь передается
на вход 2, т.е.
и обратно
.
Это возможно только тогда, когда
,
,
а
.
Таким образом, матрица рассеяния
идеального, недиссипативного, взаимного
четырехполюсника есть:
При наличии потерь,
но сохранении свойства взаимности
.
2.3. Экспериментальное определение матрицы рассеяния реального четырехполюсника
Для определения матрицы рассеяния необходимо собрать схему, изображенную на рис. 2.
Измерение
производится методом измерения
на входе четырехполюсника при известном
коэффициенте отражения
от нагрузки. Коэффициент отражения
равен отношению напряженностей
электрических полей отраженной и
падающей волны:
на входе
четырехполюсника
;
а коэффициент
отражения от нагрузки
.
По определению
коэффициент стоячей волны напряжения
(
):
.
Используя матрицу рассеяния четырехполюсника можно записать:
С учетом обозначений, приведенных на рис.l:
(4)
Из второго уравнения (4) имеем
или
,
и, подставив в первое уравнение, получим:
(5)
Таким образом,
измеряя
при разных значениях
,
можно определить все элементы матрицы
рассеяния.
Пусть:
1. К входу 2 подключена
согласованная нагрузка, т.е.
.
Тогда коэффициент отражения
четырехполюсника в плоскости 1 (рис. 1)
.
2. Вход 2 закорочен,
т.е.
,
тогда коэффициент отражения
четырехполюсника в плоскости 1
.
3. К входу 2 подключен
четвертьволновый закороченный отрезок
волновода, т.е.
,
коэффициент отражения четырехполюсника
в плоскости 1 равен
.
При действительных
,
,
,
решение уравнений зависит от отношения
и
,
т.е. от знака
.
Поскольку вход 2
четырехполюсника замкнут, т.е.
,
то при отсутствии фазосдвигающих
элементов в четырехполюснике и
должен иметь отрицательный знак. Об
этом и говорит тот факт, что в этом
случае меняются положения максимумов
и минимумов электромагнитного поля в
измерительной линии. Следовательно,
уравнения для определения элементов
матрицы рассеяния должны быть записаны
так:
(6)
Откуда
.
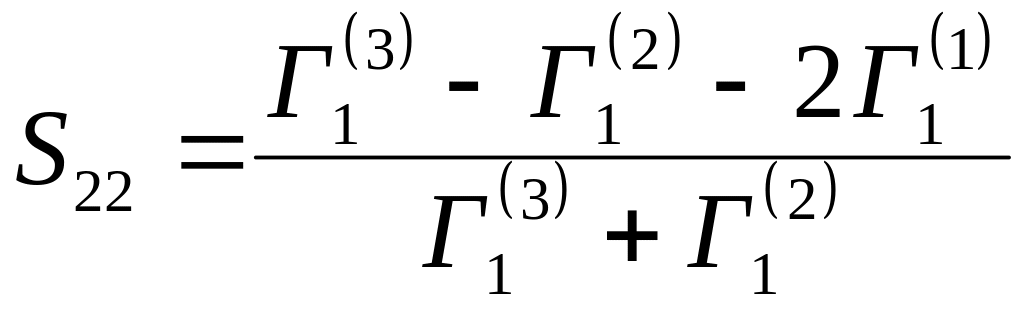
Экспериментально
можно измерить непосредственно только
частоту,
и мощность. С помощью измерительной
линии можно измерить
и длину волны. Измерения
производятся путем измерения тока
детектора в максимуме
и в минимуме
электрического поля в волноводе при
перемещении зонда. При квадратичном
детектировании, условия которого
выполняется при малых уровнях мощности
в волноводе
Или
Откуда
Измерив длину
волны в волноводе
по расстоянию между максимумами или
минимумами электрического поля и зная,
что в волноводе возбуждается волна
,
определяем длину волны (следовательно,
и частоту) в свободном пространстве:
;
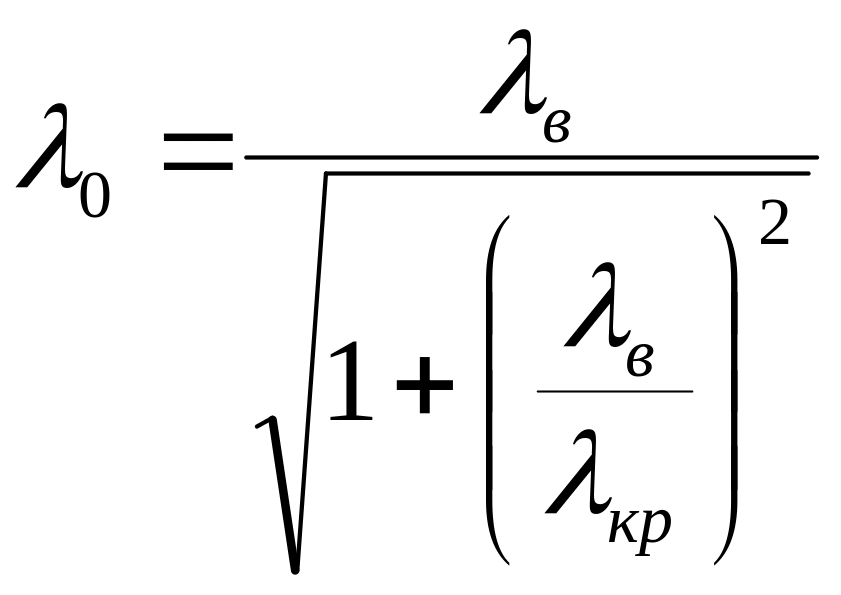а
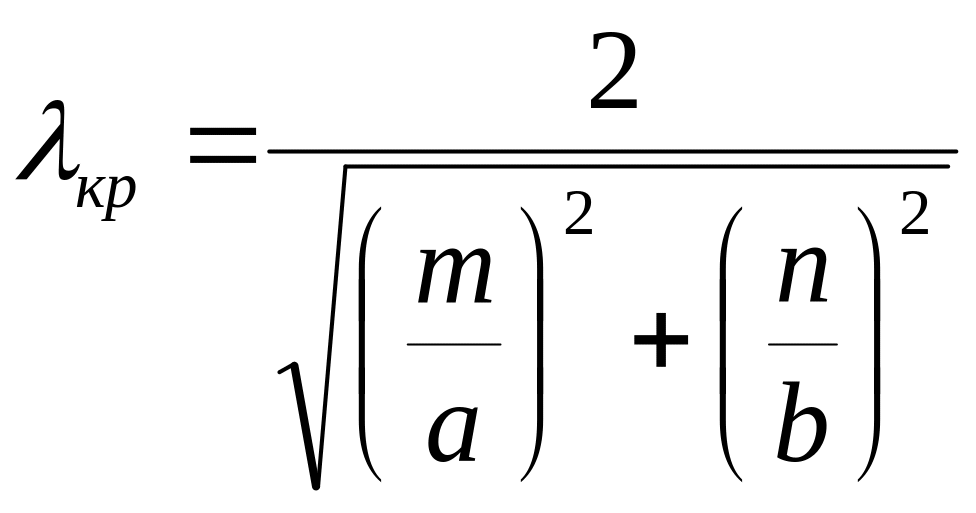
В случае
распространения волны
:
,
где
-
размер широкой стенки волновода.
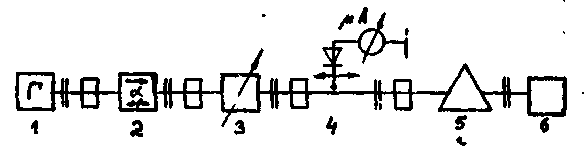
Рис.2. Схема измерений элементов матрицы рассеяния:
1 - генератор; 2 - вентиль; 3 - аттенюатор развязки; 4 - измерительная линия; 5- четырехполюсник; 6 – нагрузка с коэффициентом отражения