4.2.2. Взаимодействие модулированного электронного потока с полем резонатора. Электронная проводимость

Мощность, отдаваемая первой гармоникой конвекционного тока, в зазоре шириной при взаимодействии с переменным полем вычисляется так:

, (9)

где , - комплексные амплитуда тока и напряжение в зазоре;

; . (10)

Вычисляя интеграл (9) с учетом (10) получим выражение для активной и реактивной составляющих мощности:

(11)

. (12)

Активная составляющая мощности характеризует среднюю за период мощность, отдаваемую (или получаемую) потоком. При мощность отдается от потока полю, следовательно, в клистроне могут возбуждаться колебания. Условие самовозбуждения клистрона из (11) получается в виде:

. (13)

Это неравенство выполняется при углах пролета

,

- номер зоны генерации,

При углах пролета мощность взаимодействия максимальна. Используя (5) с учетом того, что ( - расстояние от сетки

резонатора до отражателя), , получим уравнение для напряжения на отражателе, соответствующее максимуму мощности

. (14)

Если обратиться к эквивалентной схеме зазора с модулированным по плотности электронным потоком, то сгусткам, взаимодействующим с полем резонатора, соответствует линейный двухполюсник, который описывается электронной проводимостью. Электронная проводимость определяется как отношение комплексной амплитуды тока к комплексной амплитуде напряжения на сетках, либо через мощность взаимодействия ,

.

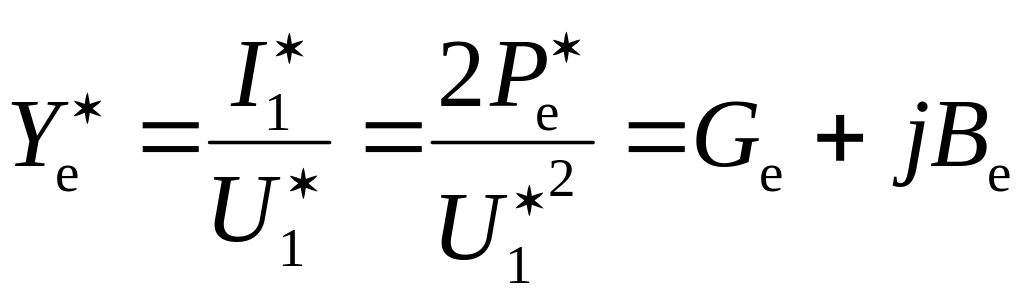Она зависит через параметр группировки от амплитуды колебаний, что косвенно учитывается нелинейностью системы. Активная составляющая электронной проводимости:

. (15)

Реактивная составляющая

, или . (16)

Зависимость определяется функциями и , и имеет вид нарастающей по амплитуде осциллирующей кривой. При углах пролета электронная проводимость чисто активна и отрицательна. Это означает, что электронные сгустки проходят зазор в моменты, когда тормозящее поле максимально. При углах электронная проводимость чисто активна и положительна. Сгустки попадают в максимум ускоряющего поля. При электронная проводимость имеет чисто реактивный характер. Во всех промежуточных случаях электронная проводимость носит комплексный характер.

4.2.3. Условие самовозбуждения. Режим автоколебаний

Самовозбуждение генератора происходит в том случае, когда мощность, отдаваемая электронным потоком, будет достаточна для компенсации потерь в резонаторе. Объединяя в одной схеме двухполюсник (зазор резонатора с электронным потоком в нем) и модель резонатора (параллельный контур) получим эквивалентную линеаризованную схему отражательного клистрона (рис. 8), - проводимость внешней нагрузки. Из линейной теории известно, что самовозбуждение возможно, если при бесконечно малых амплитудах активная проводимость двухполюсника отрицательна. Следовательно,

(17)

Эти уравнения определяют амплитуду и частоту, соответственно, установившихся колебаний. Уравнения для амплитуды колебаний с учетом (15) имеют вид

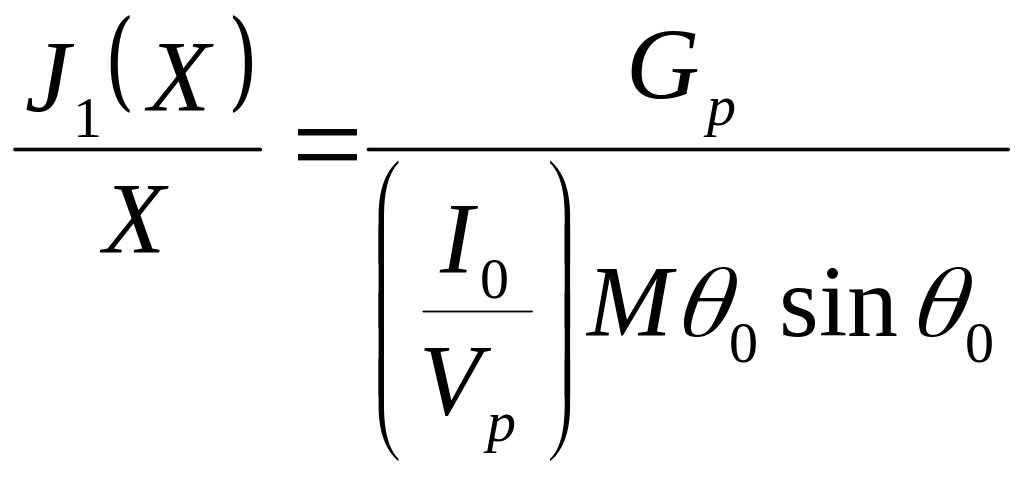. (18)

Графическое решение (18) приведено на рис. 9. Точка пересечения прямой с кривой дает установившееся значение параметра , а значит и амплитуды . Нетрудно видеть, что условие самовозбуждения колебаний в клистроне (решение формулы 18) запишется так:

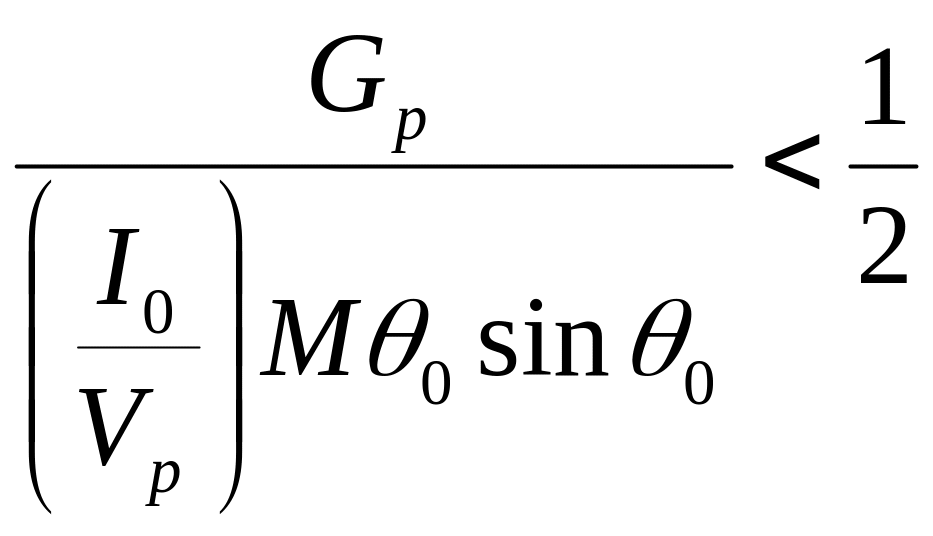(20)

или

.

Из этих условий найдем минимальную величину постоянной составляющей тока , необходимую для самовозбуждения колебаний в клистроне. Это так называемый пусковой ток:

.

Для оптимального режима пусковой ток равен

.

Рабочий ток клистрона превышает пусковой в 2-3 раза.

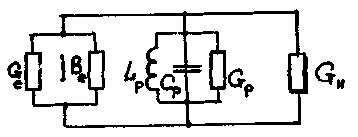
Рис. 8. Эквивалентная схема отражательного клистрона

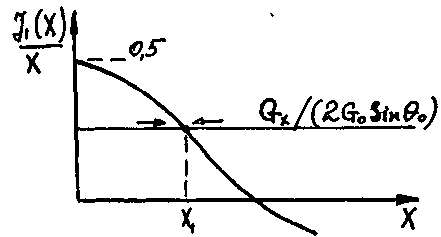
Рис. 9. Графическое определение амплитуды колебаний

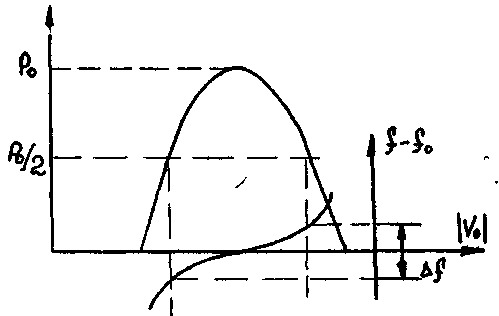
Рис. 10. Зона колебаний и электронная перестройка частоты клистрона

Процесс установления колебаний в клистроне можно представить следующим образом. Шумы возбуждают флуктуационные колебания в резонаторе и на частотах в полосе его пропускания. Возникшие слабые колебания вызывают модуляцию скорости электронов с последующей группировкой. Если условие самовозбуждения выполнено, то вернувшиеся в резонатор сгустки поддерживают колебания. Процесс нарастания амплитуды прекращается из-за возникающих нелинейностей и останавливается при равенстве электронной проводимости и проводимости контура.

При оптимальном угле пролета (центр зоны колебаний) имеет наибольшее значение и прямая (рис. 9) занимает самое низкое положение, что соответствует наибольшей амплитуде колебаний. При отклонении от оптимального уменьшается, прямая перемещается вверх, и соответствующая амплитуда колебаний уменьшается. Физически это связано с тем, что электронные сгустки встречают меньшее тормозящее поле в зазоре. На границе зоны возбуждения амплитуда падает до нуля. Граничное значение и соответствующее ему напряжение отражателя определяется из условия

.

Таким образом, зависимость мощности колебаний от напряжения отражателя в пределах одной зоны имеет экстремальный характер (рис. 4).