Хід роботи

Маючи еталонну модель , для заданого об’єкта :

1. Побудувати в пакеті SIMULINK систему адаптації до зміни постійної часу.

2. Побудувати в пакеті SIMULINK систему адаптації до зміни коефіцієнта підсилення.

3. Вивести отримані результати в пакеті MATLAB.

4. Отримані графіки оформити в пакеті MATLAB.

Варіант 1 ,

Варіант 2 ,

Варіант 3 ,

Варіант 4 ,

Варіант 5 ,

Варіант 6 ,

Варіант 7 ,

Варіант 8 ,

Варіант 9 ,

Варіант 10 ,

Контрольні запитання

1. Що таке адаптивна система?

2. Намалюйте загальну структурну схему адаптивної системи.

3. Що таке параметричні збурення?

4. Що таке координатні збурення?

5. Намалюйте структурну схему системи адаптації до зміни коефіцієнта підсилення.

6. Намалюйте структурну схему системи адаптації до зміни постійної часу.

7. Що таке еталонна модель?

8. Яку роль виконує алгоритм ідентифікації в схемі адаптивної системи?

9. Яку роль виконує алгоритм адаптації в схемі адаптивної системи?

10. Із яких контурів складається кожна адаптивна система?

Лабораторна робота 20 Робастні системи управління

Мета роботи: ознайомитись із поняттям „робастні системи”, навчитись виконувати синтез робастних систем, визначати Н_∞-норму, що є мірою робастності та Н₂-норму, що є мірою якості робастних систем.

Основні теоретичні відомості

Робастними називаються автоматичні системи, що дозволяють зберігати стійкість та підтримувати показник якості в допустимих межах при дії на систему параметричних збурень без використання методів адаптації.

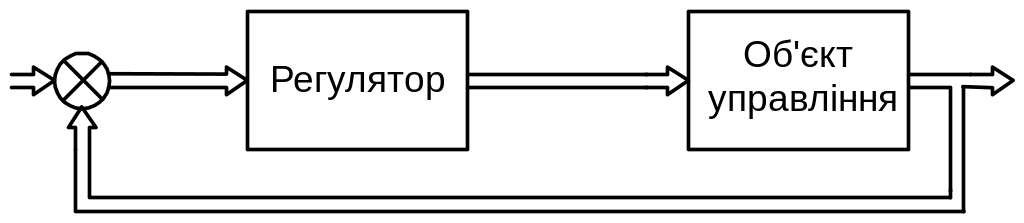
Рис.20.1. Структурна схема замкненої системи

Для обчислення показників якості робастних систем управління використовується -норма.

Для стійкої неперервної системи із передавальною функцією Н(s) ця норма являє собою квадратний корінь із середнього значення квадрата імпульсної перехідної функції системи. При використанні перетворення Лапласа відповідно до теореми Парсеваля -норма визначається співвідношенням

(20.1)

Цю норму можна представити, як коваріацію вихідного сигналу в усталеному стані за умови впливу на систему «білого шуму» з одиничною інтенсивністю

(20.2)

. (20.3)

Показник якості управління можна розрахувати за допомогою функції Грама, або так званого граміана керованості. Граміани керованості застосовуються для дослідження властивостей управління моделей систем, заданих у просторі станів, а також для побудови їхніх мінімальних реалізацій. Вони є більш зручним для проведення математичних розрахунків у порівнянні із матрицями управління.

Для моделі неперервної системи у просторі станів

(20.4)

граміан керованості визначається інтегралом

. (20.5)

Для дискретних моделей аналогом граміана керованості є вираз

. (20.6)

Граміан керованості є додатньо визначений тоді і тільки тоді, коли пара матриць {A, B} є керованими. Граміан керованості обчислюється шляхом розв’язання неперервного рівняння Ляпунова

, (20.7)

або його дискретного аналога

. (20.8)

Обмеженням є те, що матриця А повинна бути стійкою, тобто для неперервних моделей усі корні характеристичного рівняння мають бути від’ємними, а для дискретних – строго меншими одиниці за модулем.

Для визначення -норми засобами MatLAB використовуються команди визначення граміана керованості (gram), розв’язання рівняння Ляпунова (lyap), визначення сліду матриці (trace).

Gd=gram(Acs,Bcs);

Jd=trace(Cd*Gd*Cd');

Обчислення -норми можна здійснити у такий спосіб:

h2_n=normh2(Acs,Bcs,Cexd,Dex)

Показник норми є нескінченим для наступних випадків:

_{1) модель є нестійкою;}

_{2) модель неперервної системи має ненульову матрицю D.}

Величина -норми є мірою якості (точності). До неї відноситься функція чутливості S(s), що виражається співвідношенням:

_{, (20.9)}

де – передавальна функція об'єкта;

– передавальна функція регулятора.

Мірою робастності замкненої системи є Н_-норма - функція комплементарної чутливості Т(s). Така чутливість є передавальною функцією (для одновимірних систем) або матрицею передавальних функцій (для багатовимірних систем) замкненої системи (див. рис.20.1), в якій регулятор та об’єкт знаходяться у прямому зв’язку та має місце одиничний зворотний зв’язок:

. (20.10)

У теорії управління існує відоме співвідношення між якістю системи та її робастністю

. (20.11)

Функція S(s) є функцією чутливості по відношенню до координатних збурень, а функція T(s) визначає чутливість системи щодо параметричних збурень.

Очевидно, що це співвідношення дозволяє досягти компромісу між якістю і робастністю системи. У відповідності із (20.11), збільшуючи робастність, ми втрачаємо якість, і, навпаки, підвищуючи якість, втрачаємо робастність.

Чисельне значення Н_-норми дорівнює максимальному значенню модуля частотної характеристики і визначається таким чином:

– для одновимірних моделей

, (20.12)

– для багатовимірних моделей

. (20.13)

де: - сингулярне число матриці Н, - максимальне сингулярне число на заданій частоті.

Залежність називається сингулярною частотною характеристикою багатовимірної замкненої системи. Вона визначає запаси стійкості за амплітудою та фазою системи. Підтримання -норми функції комплементарної чутливості для різних параметрично збурених моделей об’єкта управління гарантує певну нечутливість щодо параметричних збурень у всьому діапазоні допустимих параметрів польоту.

Н_-норма дорівнює нескінченності, якщо неперервна модель має полюси на уявній осі або дискретна моделі має полюси на колі одиничного радіуса.

За допомогою засобів MATLAB Н_ -норму можна визначити у такий спосіб:

Hinf_n=normhinf(Acs,Bcs,Cexd,Dex)

Як відомо, при зменшенні -норми, - норма зростає та навпаки. Тому вимоги до точності та якості управління з однієї сторони та робастності з іншої сторони є взаємно суперечливими, а задача синтезу системи управління полягає у відшуканні компромісу між якістю і робастністю системи. Ця мета досягається об’єднанням обох показників в одному комплексному критерії із ваговими коефіцієнтами. Змінюючи ці коефіцієнти під час процедури оптимізації можна досягти бажаного компромісу.