Контрольні запитання
1. За допомогою якого оператора можна аналітично побудувати детермінований оптимальний регулятор?
2. За допомогою якого оператора можна порахувати показник якості системи?
3. За допомогою якого оператора можна побудувати перехідну характеристику системи?
4. За допомогою якого оператора можна побудувати імпульсну характеристику системи?
5. Як задаються системи у просторі станів?
6. Яким умовам повинні задовольняти матриці A, B, C, D, щоб сформувати систему у просторі станів?
7. Яким чином відбувається з’єднання блоків, що задані моделлю у просторі станів?
8. Поясніть алгоритм синтезу оптимального стохастичного спостерігача .
9. За допомогою якого оператора можна отримати стохастичний оптимальний спостерігач?
10. Що ви розумієте під терміном „відновлення стану системи”?
11. Які оператори використовувались в даній лабораторній роботі?
Лабораторна робота 18 Оптимальний лінійний стохастичний регулятор при неповних вимірах. Теорема розділення
Мета роботи: навчитись відновлювати вектор стану системи при стохастичних збуреннях та неповних вимірах, використовувати теорему розділення.
Основні теоретичні відомості
Розглянемо задачу оптимального лінійного регулювання, коли спостереження системи є неповними та неточними, тобто коли виміряти повний вектор стану не можна, а доступні виміри містять шум. Крім того, допускається, що на систему діють випадкові збурення.
Розглянемо систему
.
Спостережувана змінна описується виразом
.
Сумісний випадковий
процес
є білим шумом з інтенсивністю
.
Тоді задача
стохастичного лінійного оптимального
регулювання із зворотнім зв’язком по
вихідній змінній є задачею знаходження
такого оператора
при якому критерій
досягає мінімуму.
тут
- симетричні вагові матриці.
Рішення цієї задачі є комбінацією рішень задачі детермінованого оптимального регулювання і задачі оптимального стохастичного відновлення. Це твердження відоме як теорема розділення. Запишемо детальніше рішення задачі стохастичного лінійного регулювання із зворотнім зв’язком по вихідній змінній. Для вихідної змінної маємо
, (18.1)
де
.
Тут
– рішення алгебраїчного рівняння
Ріккаті
Оцінку
отримуємо як рішення рівняння
, (18.2)
де . Матриця дисперсій є рішенням рівняння Ріккаті
.
На рис.18.1. представлено взаємозв’язок об’єкта, спостерігача та регулятора.. Підставивши вираз для закону управління (18.1) в рівняння спостерігача (18.2), отримаємо рівняння регулятора
,
.
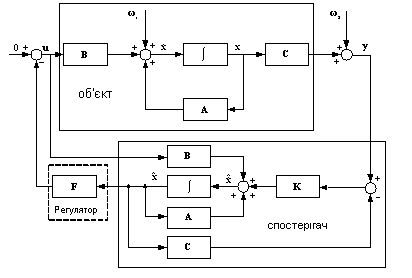Рис.18.1.
З’єднання об’єкта, спостерігача та
регулятора
Завдяки цьому ми
маємо спрощену структуру.
На рис.18.2.
приведена блок-схема цієї стохастичної
оптимальної системи управління із
зворотнім зв’язком по вихідній змінній.
Замкнена система, отримана в результаті
з’єднання об’єкта з регулятором,
представляє собою лінійну систему
розмірності
,
де
- розмірність стану
,
яку можна описати рівнянням
Таким чином, на першому етапі синтезується оптимальний стохастичний спостерігач. Вхідними даними для синтезу є збурений (розширений) об’єкт та матриці коваріацій шумів. В результаті отримаємо модель спостерігача в просторі стану.
На другому етапі здійснюється синтез оптимального детермінованого регулятора.
Вхідними даними для синтезу є матриця стану розширеного об’єкта, частина матриці управління розширеного об’єкта (вибираємо тільки ті стовпчики, які відповідають керованим входам) та матриці вагових коефіцієнтів. В результаті потримаємо коефіцієнти підсилений регулятора.
З метою одержання спрощеного регулятора на третьому етапі здійснюється поєднання спостерігача з регулятором.
Рис. 18.2. Оптимальний лінійний регулятор при неповних вимірах, які мають шум
В пакеті програм MATLAB можна вирішити дану задачу, виконавши даний алгоритм.
1. В просторі стану задати четвірку матриць об’єкта. Задаємо матрицю B0 для входу управління та матрицю Bg0 для входу збурень. Матриця спостережень C0 має неповний ранг, тобто ми можемо виміряти лише 3 виходи системи.
Vt=69.4444;
A0=[-0.0345 5.9942 -9.7764 0 0;
-0.0041 -1.7565 0 0.9860 0;
0 0 0 1.0000 0;
0.0033 -25.6814 0 -2.1905 0;
0 -Vt Vt 0 0];
B0 =[0.3576 -0.1628 0 -31.1037 0]';
Bg0=[-0.0345 5.9942 0;
-0.0041 -1.7565 0.9860;
0 0 1.0000;
0.0033 -25.6814 -2.1905;
0 0 0];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1];
D0=zeros(3,1);
2. В просторі стану задати четвірку матриць виконавчого механізму. Зробити послідовне з’єднання виконавчого механізму та об’єкту. Виділити четвірку матриць отриманого з’єднання:
Ta=0.5;
sysac=ss(-1/Ta,1/Ta,1,0);
sysai=ss(A0,B0,C0,D0);
sysh2=series(sysac,sysai);
3. Задаємо четвірку матриць формуючого фільтру( по моделі Драйдена).
ag=[-0.12 0 0; 0 0 1; 0 -0.0143 -0.2394];
bg=[0.5522 0; 0 0; 0 1];
cg=[1 0 0; 0 6.7e-4 0.0097; 0 1.39e-4 1.65e-3];
dg=[0 0; 0 0; 0 -0.0097];
4. Включаємо формуючий фільтр в структуру об’єкта.
Dex=zeros(3,4);
Bex=[B0,Bg0];
aircex=ss(A0,Bex,C0,Dex);
sysinp=append(sysac,formsys);
stsys=series(sysinp,aircex);
[Ast,Bst,Cst,Dst]=ssdata(stsys);
5. Синтез фільтру Калмана
disp('Kalman Filter')
V1=eye(2);
V=[0.25, 0.01, 25];
V2=diag(V);
[kest,l,p]=kalman(stsys,V1,V2);
[Aest,Best,Cest,Dest]=ssdata(kest);
6. Коли стан системи відновлено, можна приміняти закони синтезу оптимального детермінованого регулятора.
R1=[0.1 0.1 1.5 0.01 1 0.1 0.01 0.01 0.01];
R1=diag(R1);
R2=0.1;
[K,S,E]=lqr(Ast,Bst(:,1),R1,R2)
7. Поєднання оптимального стохастичного спостерігача (фільтра Калмана) та оптимального детермінованого регулятора здійснюється за допомогою оператора lqgreg.
F=lqgreg(kest,K);
[Ar,Br,Cr,Dr]=ssdata(F);
8. Замикаємо об’єкт регулятором, подаючи управління на вхід 1, а на регулятор подаємо виходи [1,2,3] об’єкта. Так як мінус зворотного зв’язку враховується при з’єднанні спостерігача з детермінованим регулятором, ми замикаємо систему додатнім зворотнім зв’язком. Оператором eig рахуємо власні числа системи.
cl=feedback(stsys,F,1,[1,2,3],1); Aopt=eig(cl)
[Ao,Bo,Co,Do]=ssdata(cl);
9. Будуємо перехідні характеристики замкненої системи.
figure(1)
impulse(cl(:,1))
figure(2)
step(cl(:,1))
10. Для розрахунку - норми стохастичної системи робимо послідовне з’єднання регулятора з об’єктом без формуючого фільтра
st2=series(F,sysh2);
st3=feedback(st2,eye(3),1);
[a,b,c,d]=ssdata(st3);
H2n=normh2(a,b,c,d)
Завдання
Необхідно використавши теорему розділення синтезувати стохастичну оптимальну систему управління.
Дано чотири матриці , які описують динаміку літака, четвірку матриць виконавчого механізму, а також четвірку матриць формуючого фільтру.
Алгоритм синтезу викладений вище.
Варіант 1
Об’єкт:
Vt=69.44;
A=[-0.136 0.1403 0.0001 -0.9986 0;
0 0 1.003 0 0;
-56.21 0 -11.25 3.332 0;
1.190 0 -0.210 -0.240 0;
0 Vt -Vt 1 0];
B=[0 0 160 0 0 ]';
Bg0=[-0.136 -0.9986;
0 0 ;
-56.21 3.332 ;
1.190 -0.240 ;
0 1];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1];
D=zeros(3,1);
Формуючий фільтр:
ag=[0 1 0; -0.0144 -0.24 0; 0.011/4 0.131/4 -39.37];
bg=[0 1 -0.767]';
cg=[0.344 0.1947 0; 0 0 1];
dg=[0 0]';
Варіант 2
Об’єкт:
Vtp=55.56;
Ap=[-0.109 0.1754 0.0001 -0.9988 0;
0 0 1.003 0 0;
-36.2778 0 -9.195 2.802 0;
0.8611 0 -0.173 -0.185 0;
0 Vtp - Vtp 1 0];
Bp=[0 0 103.62 0 0 ]';
Bg0p=[ -0.109 -0.9988;
0 0;
-36.2778 2.802;
0.8611 -0.185;
0 1];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1];
D=zeros(3,1);
Формуючий фільтр:
agp=[0 1 0; -9.2e-3 -0.192 0; 6.32e-3 0.0938 -31.5];
bgp=[ 0 1 -0.685]';
cgp=[ 0.09 0. 217 0; 0 0 1];
dgp=[0 0]';
Варіант 3
Об’єкт:
Vt=69.4444;
A0=[-0.0345 5.9942 -9.7764 0 0;
-0.0041 -1.7565 0 0.9860 0;
0 0 0 1.0000 0;
0.0033 -25.6814 0 -2.1905 0;
0 -Vt Vt 0 0 ];
B0 =[0.3576 -0.1628 0 -31.1037 0]';
Bg0=[-0.0345 5.9942 0;
-0.0041 -1.7565 0.9860;
0 0 1.0000;
0.0033 -25.6814 -2.1905;
0 0 0];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1] ;
D0=zeros(3,1);
Формуючий фільтр:
ag=[-0.12 0 0; 0 0 1; 0 -0.0143 -0.2394];
bg=[0.5522 0; 0 0; 0 1];
cg=[1 0 0; 0 6.7e-4 0.0097; 0 1.39e-4 1.65e-3];
dg=[0 0; 0 0; 0 -0.0097];
Варіант 4
Об’єкт:
Vtp=55.5556;
A0p=[-0.0273 5.9960 -9.7764 0 0;
-0.0064 -1.3927 0 0.9971 0;
0 0 0 1.0000 0;
0.0036 -16.1243 0 -1.7339 0;
0 -Vtp Vtp 0 0 ];
B0p=[0.3581 -0.1303 0 -19.8857 0]';
Bg0p=[-0.0273 5.9960 0;
-0.0064 -1.3927 0.9971;
0 0 1.0000;
0.0036 -16.1243 -1.7339;
0 0 0];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1] ;
D0=zeros(3,1);
Формуючий фільтр:
agp=[-0.096 0 0; 0 0 1; 0 -0.0092 -0.192];
bgp=[0.4939 0; 0 0; 0 1];
cgp=[1 0 0; 0 6.05e-4 0.011; 0 1.01e-4 1.5e-3];
dgp=[0 0; 0 0; 0 -0.011];
Варіант 5
Об’єкт:
A =[ -0.1360 0.1403 0.0001 -0.9986;
0 0 1.0030 0;
-56.21 0 -11.2500 3.3320;
1.190 0 -0.2100 -0.2400]
Bu=[0 0 160 0 ]';
Bg=[-0.136 -0.9986;
0 0 ;
-56.21 3.332 ;
1.190 -0.240 ];
C=eye(4); D=zeros(4,1);
Формуючий фільтр:
ag=[0 1 0; -0.0144 -0.24 0; 0.011/4 0.131/4 -39.37];
bg=[0 1 -0.767]';
cg=[0.01344 0.1947 0; 0 0 1];
dg=[0 0]';
Варіант 6
Об’єкт:
Ap =[-0.1090 0.1754 0.0001 -0.9988;
0 0 1.0030 0;
-36.2778 0 -9.1950 2.8020;
0.8611 0 -0.1730 -0.1850]
Bup=[0 0 103.62 0 ]';
Bgp=[ -0.109 -0.9988;
0 0;
-36.278 2.802;
0.8611 -0.185];
C=eye(4); D=zeros(4,3);
Формуючий фільтр:
agp=[0 1 0; -9.2e-3 -0.192 0; 6.32e-3/4 0.0938/4 -31.5];
bgp=[ 0 1 -0.685/4]';
cgp=[ 1.2 0.0217/4 0; 0 0 1];
dgp=[0 0]';
Варіант 7
Об’єкт: Vt=55;
A=[-0.136 0.1403 0.0001 -0.9986 0;
0 0 1.003 0 0;
-56.21 0 -11.25 3.332 0;
1.190 0 -0.210 -0.240 0;
0 Vt -Vt 1 0];
B=[0 0 160 0 0 ]';
Bg0=[-0.136 -0.9986;
0 0 ;
-56.21 3.332 ;
1.190 -0.240 ;
0 1];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1];
D=zeros(3,1);
Формуючий фільтр:
ag=[0 1 0; -0.0144 -0.24 0; 0.011/4 0.131/4 -39.37];
bg=[0 1 -0.767]';
cg=[0.01344 0.1947 0; 0 0 1];
dg=[0 0]';
Варіант8.
Об’єкт:
Vtp=64,99;
Ap=[-0.109 0.1754 0.0001 -0.9988 0;
0 0 1.003 0 0;
-36.2778 0 -9.195 2.802 0;
0.8611 0 -0.173 -0.185 0;
0 Vtp - Vtp 1 0];
Bp=[0 0 103.62 0 0 ]';
Bg0p=[ -0.109 -0.9988;
0 0;
-36.2778 2.802;
0.8611 -0.185;
0 1];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1];
D=zeros(3,1);
Формуючий фільтр:
agp=[0 1 0; -9.2e-3 -0.192 0; 6.32e-3 0.0938 -31.5];
bgp=[ 0 1 -0.685]';
cgp=[ 0.09 0. 217 0; 0 0 1];
dgp=[0 0]';
Варіант 9
Об’єкт:
Vt=55,5444;
A0=[-0.0345 5.9942 -9.7764 0 0;
-0.0041 -1.7565 0 0.9860 0;
0 0 0 1.0000 0;
0.0033 -25.6814 0 -2.1905 0;
0 -Vt Vt 0 0 ];
B0 =[0.3576 -0.1628 0 -31.1037 0]';
Bg0=[-0.0345 5.9942 0;
-0.0041 -1.7565 0.9860;
0 0 1.0000;
0.0033 -25.6814 -2.1905;
0 0 0];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1] ;
D0=zeros(3,1);
Формуючий фільтр:
ag=[-0.12 0 0; 0 0 1; 0 -0.0143 -0.2394];
bg=[0.5522 0; 0 0; 0 1];
cg=[1 0 0; 0 6.7e-4 0.0097; 0 1.39e-4 1.65e-3];
dg=[0 0; 0 0; 0 -0.0097];
Варіант 10
Об’єкт:
Vtp=64,999;
A0p=[-0.0273 5.9960 -9.7764 0 0;
-0.0064 -1.3927 0 0.9971 0;
0 0 0 1.0000 0;
0.0036 -16.1243 0 -1.7339 0;
0 -Vtp Vtp 0 0 ];
B0p=[0.3581 -0.1303 0 -19.8857 0]';
Bg0p=[-0.0273 5.9960 0;
-0.0064 -1.3927 0.9971;
0 0 1.0000;
0.0036 -16.1243 -1.7339;
0 0 0];
C0=[ 0 0 1 0 0; 0 0 0 1 0; 0 0 0 0 1] ;
D0=zeros(3,1);
Формуючий фільтр:
agp=[-0.096 0 0; 0 0 1; 0 -0.0092 -0.192];
bgp=[0.4939 0; 0 0; 0 1];
cgp=[1 0 0; 0 6.05e-4 0.011; 0 1.01e-4 1.5e-3];
dgp=[0 0; 0 0; 0 -0.011];