Изучение основных элементов виброизмерительной аппаратуры и измерение вибрации роторных машин

1. Колебания машин.

1.1. Введение в колебания и вибрацию машин и механизмов.

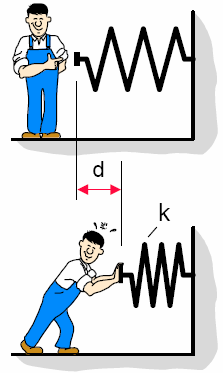
Вибрация – это колебания относительно неподвижной точки. Это результат динамических сил, проистекающих в машинах, которые имеют подвижные части. Различные части машины вибрируют на разных частотах и с различной амплитудой. Вибрация, как правило, вызывает износ и усталость механизмов, и зачастую, влияет на полный вывод механизма из работоспособного состояния.

1.2. Механические параметры и компоненты вибрации.

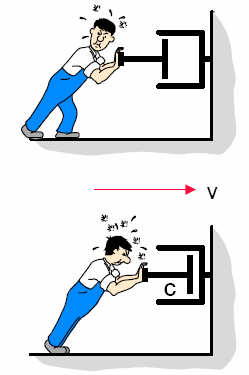
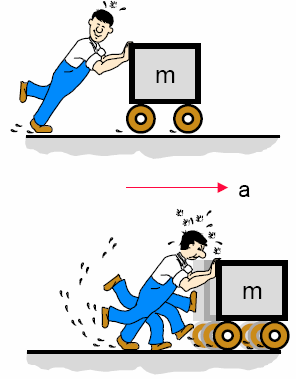
Перемещение	Скорость	Ускорение
F=kd	F=cv	F=mv

1.3. Простейшие формы вибрации систем.

Из рисунка 1.1 видно, что колебания простейшей системы, состоящей из массы и упругого элемента можно описать синусоидальной диаграммы с амплитудой (D) и периодом (T). Частота колебаний (f) определяется как величина обратно пропорциональная периоду. Произведение частоты на 2 дает нам угловую частоту пропорциональную корню отношения коэффициента пружины и массы, которая является собственной частотой данной системы.

В общем случае перемещение может быть описано как , где d – мгновенное значение, D – пиковое значение.

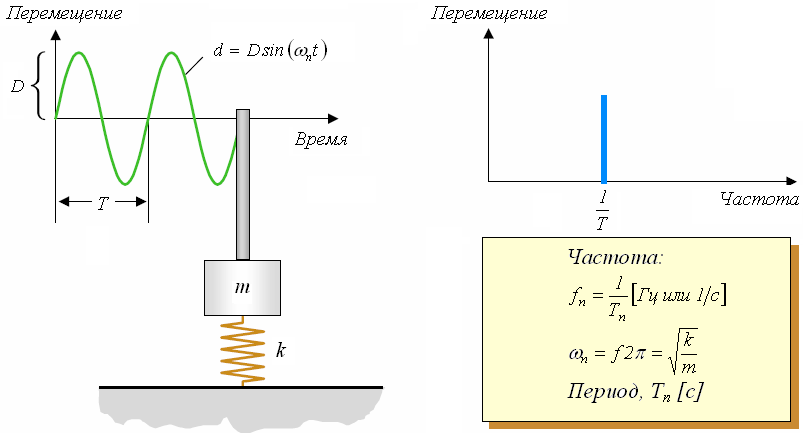
Рисунок 1.1. Колебания простейшей системы.

1.4. Колебания без демпфирования.

На рисунке 1.2. изображено колебание одномассовой системы без демпфирования (затухания). Как видно из рисунка при достижении максимума перемещения кинетическая энергия равна нулю, соответственно потенциальная энергия (скорость) имеет максимальное значение и равна . В среднем положении потенциальная энергия равна нулю, при этом кинетическая достигает максимального значения .

Для гармонических колебаний перемещения можно записать следующее

.

С помощью дифференцирования мы можем определить скорость

,

где V – пиковое значение скорости, и определяется как .

Используя закон сохранения энергии мы можем получить собственную частоту колебаний системы

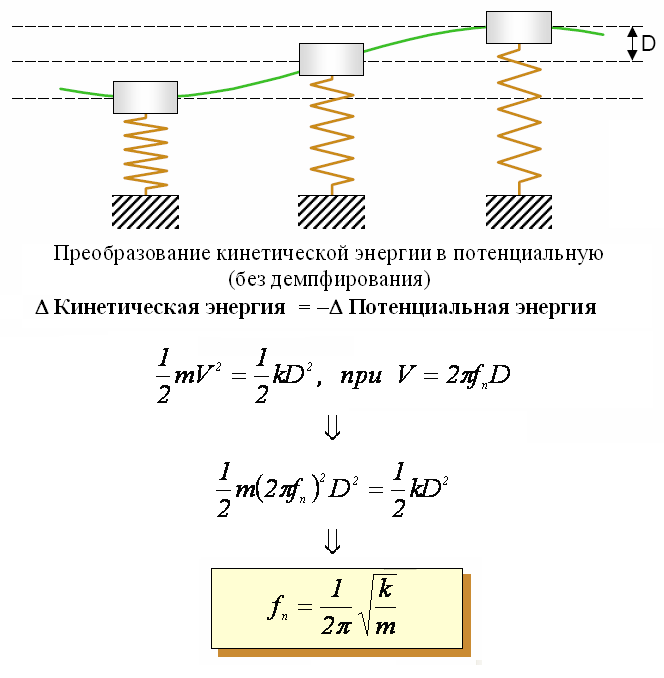
Рисунок 1.2. Колебания одномассовой системы без демпфирования.

На рисунке 1.3. изображено изменение колебаний одномассовой системы при увеличении массы. Как видно из рисунка увеличение массы приводит к уменьшению частоты и увеличению периода колебаний.

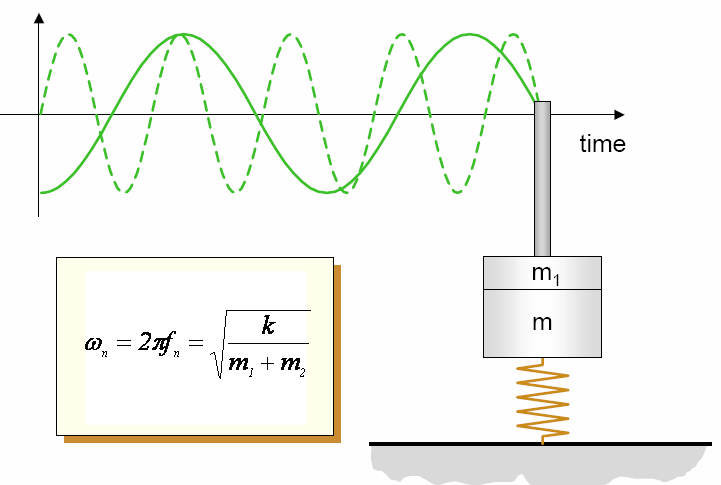
Рисунок 1.3. Колебания одномассовой системы при увеличении массы.

1.5. Колебания с демпфированием.

На рисунке 1.5. проиллюстрировано изменение колебаний одномассовой системы с демпфирующим элементом. Результатом демпфирования является снижение амплитуды колебаний во времени.

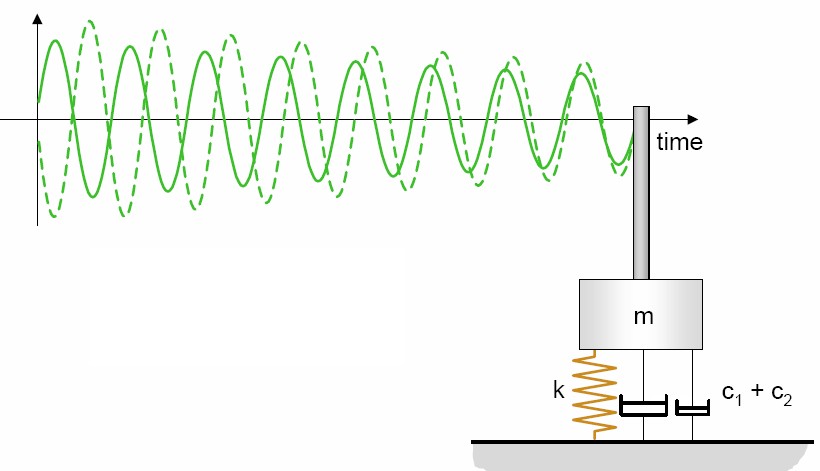
Рисунок 1.4. Колебания одномассовой системы с демпфирующим элементом.

1.6. Вынужденные колебания.

При приложении внешних сил (F) на систему, система начинает колебаться и выходить из состояния равновесия и колеблется с частотой, которую имеет внешняя сила. Но это не означает что система будет колебаться с такой же амплитудой и углом (фазой) (рисунок 1.5.а).

Как видно из рисунка в случае совпадения собственной частоты и частоты возбуждающей силы, в отсутствие демпфера может произойти явление резонанса (рисунок 1.5.б).

При увеличении частоты возмущающей силы изменяется угол (фаза) колебаний системы, а также и амплитуда колебаний (рисунок 1.5.в).

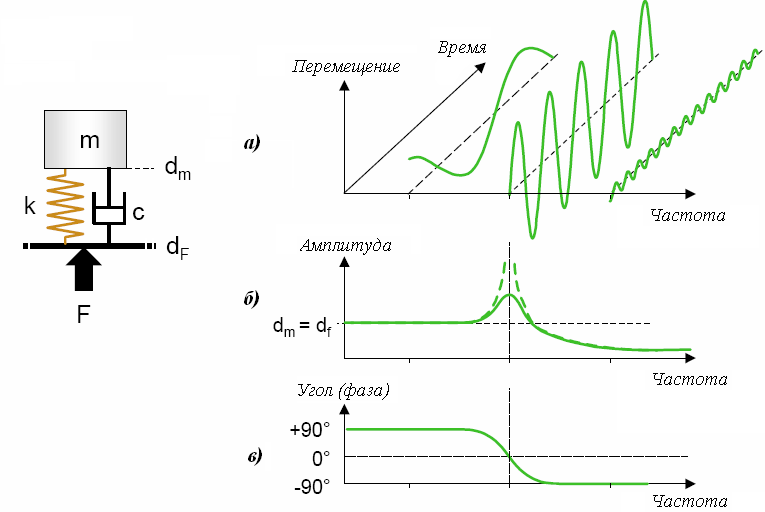
Рисунок 1.5. Вынужденные колебания.

Принимая во внимание, что реальные механические системы имеют более сложное строение, рассмотрим колебания системы, состоящей из двух простейших систем (рисунок 1.6.)

Как видно из рисунка система состоит из двух простейших систем. При воздействии внешней периодической силы обе системы начинают колебаться на собственных частотах, отличие заключается в том, что верхняя система колеблется не только относительно внешней приложенной силы, но и от воздействия на нее нижней системы. Т.е. как видно из рисунка на амплитудно ‑ частотной характеристике имеется два пиковых значения.

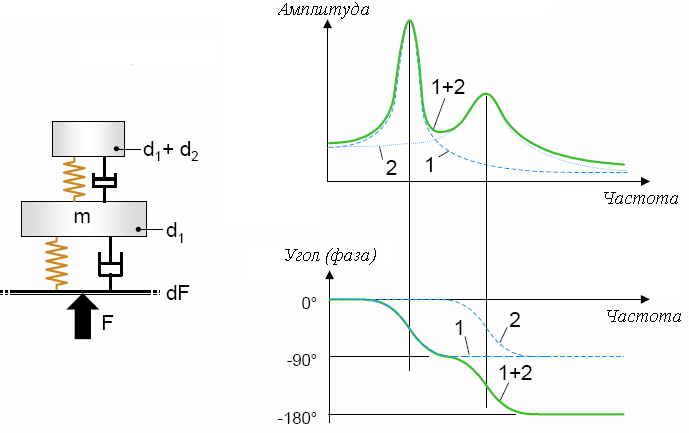
Рисунок 1.6. Колебания системы из двух простейших систем.

На рисунке 1.7 изображены система с одной и множеством степенями свободы.

Система с одной степенью свободы - система, которая может выполнять движение только в одном направлении.

В случае сложных систем движение может осуществляться во многих направлениях. В данных системах мы имеем возможность наблюдать за каждым пиком от степени свободы в амплитудно – частотной характеристике.

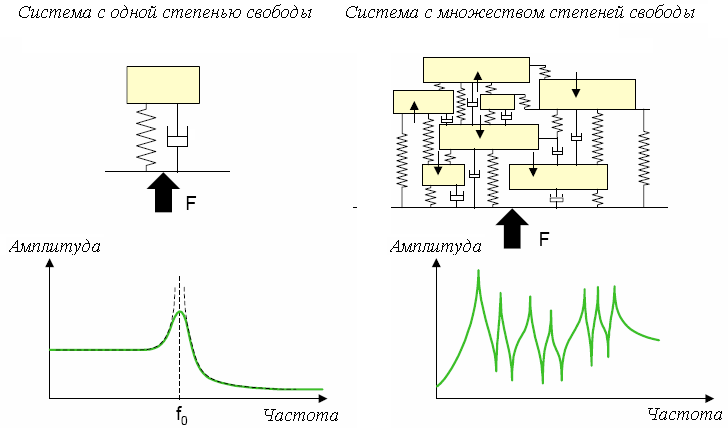
Рисунок 1.7. Колебания системы с множеством степенями свободы.

На практике же в большинстве случаев чрезвычайно сложно разделить различные механические компоненты. Это связано с тем, что каждая реальная механическая система, даже самая простейшая имеет в своем составе множество простейших систем и зачастую достаточно сложно разделить их частотные компоненты. Это можно рассмотреть на примере упрощенной схемы электродвигателя (рисунок 1.8).

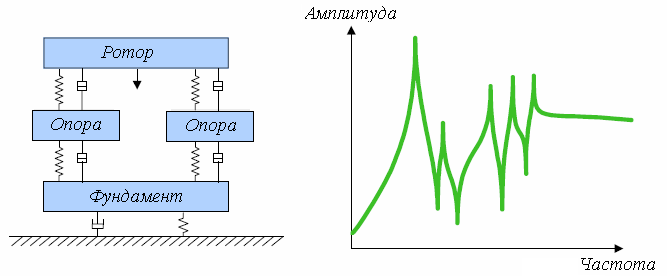
Рисунок 1.8. Упрощенная схема электродвигателя.

1.7. Вынужденные колебания и вибрация.

В реальных системах частотные характеристики являются трудно распознаваемыми, это связано с конструктивными особенностями таких систем. На рисунке 1.9 изображено влияние основных параметров системы на вибрационное состояние системы и это только для электродвигателя.

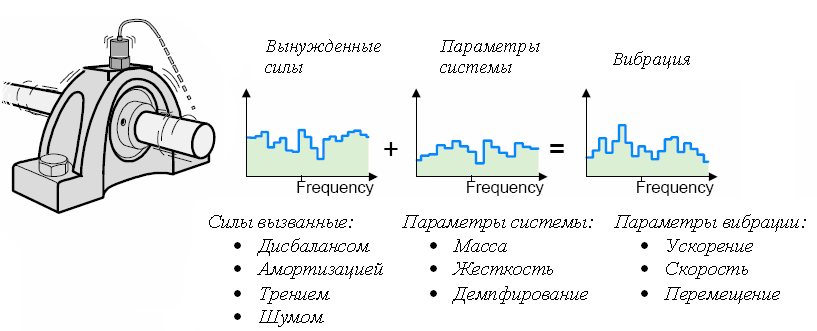
Рисунок 1.9.

1.8. Типы сигналов.

Первоначально сигналы можно разделить на две большие группы детерминированные и случайные (рисунок 1.10).

Детерминированные сигналы это сигналы, значения которых в любой момент времени или в произвольной точке пространства (а равно и в зависимости от любых других аргументов) являются заранее известными или могут быть достаточно точно определены (вычислены).

К периодическим относят гармонические и полигармонические сигналы.

К периодическим относят гармонические и полигармонические сигналы. Для периодических сигналов выполняется общее условие s(t) = s(t + kT), где k = 1, 2, 3, ... - любое целое число, Т - период, являющийся конечным отрезком времени (рисунок 1.11).

Гармонические сигналы (или синусоидальные), описываются следующими формулами:

s(t) = Asin(2f_оt+) = Asin(_оt+),

или:

s(t) = Acos(_оt+),

где А, f_o, _o,  - постоянные величины: А - амплитуда сигнала, f_о - циклическая частота в герцах, _о= 2f_о - угловая частота в радианах,  и - начальные фазовые углы в радианах. Период одного колебания T = 1/f_о = 2/_o. При  = -/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты f_о (при t = 0).

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:

s(t) = A_nsin(_nt+_n),

или непосредственно функцией s(t) = y(t  kT_p), k = 1,2,3,..., где Т_p - период одного полного колебания сигнала y(t), заданного на одном периоде. Значение f_p =1/T_p называют фундаментальной частотой колебаний. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей (f_о = 0) и произвольного (в пределе - бесконечного) числа гармонических составляющих с частотами, кратными фундаментальной частоте f_p, и с произвольными значениями амплитуд A_n и фаз _n. Другими словами, частотный спектр полигармонических сигналов дискретен, в связи с чем второе распространенное математическое представление сигналов - в виде спектров (рядов Фурье).

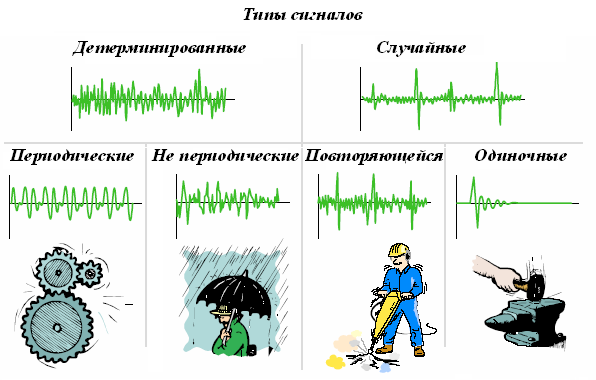
Рисунок 1.10. Типы сигналов.

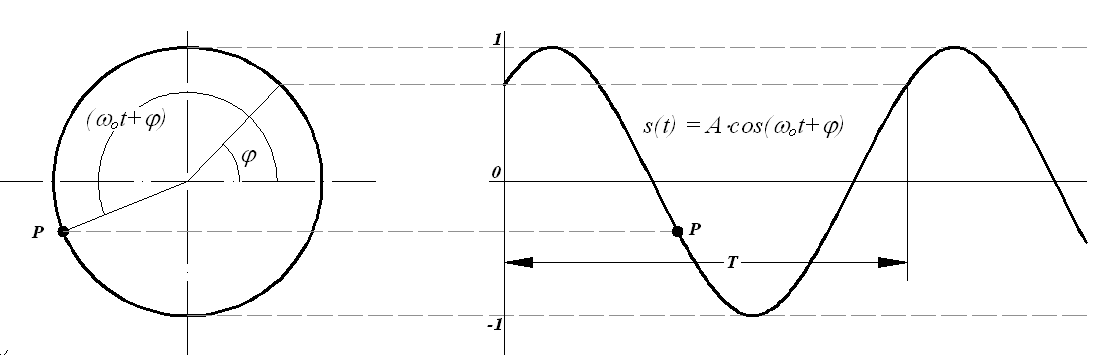
Рисунок 1.11. Периодический сигнал.

К непериодическим сигналам относят почти периодические и апериодические или переходные сигналы (рисунок 1.12).

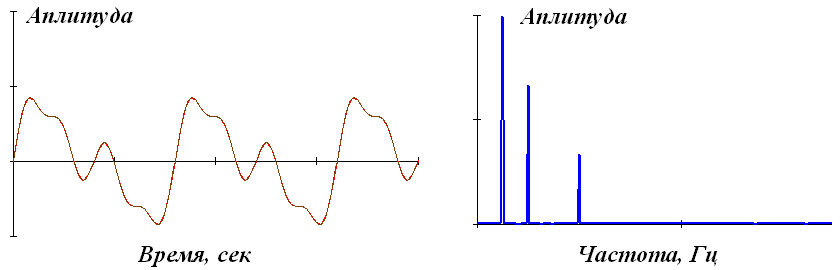
Рисунок 1.12. Почти периодический сигнал и спектр его амплитуд.

Почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов, но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На рисунке 1.13 показан пример апериодического сигнала, заданного формулой на интервале (0, ):

s(t) = exp(-at) - exp(-bt),

где a и b – константы, в данном случае a = 0.15, b = 0.17. Частотный спектр апериодических сигналов непрерывен. Для их представления в частотной области используется интегральное преобразование Фурье, которым отображается спектральная плотность сигнала.

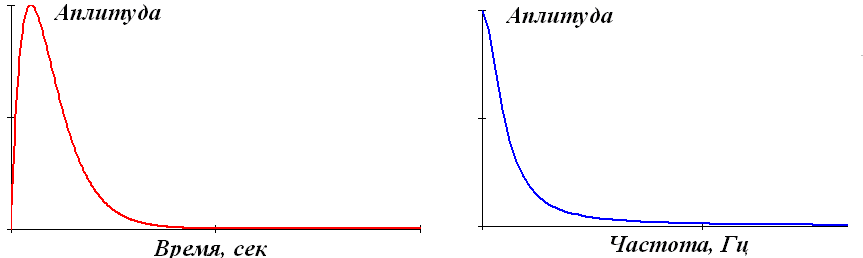
Рисунок 1.13. Апериодический сигнал и модуль его спектра.

К апериодическим сигналам относятся также импульсные сигналы, которые в радиотехнике и в отраслях, широко ее использующих, часто рассматривают в виде отдельного класса сигналов. Импульсы представляют собой сигналы, как правило, определенной и достаточно простой формы, существующие в пределах конечных временных интервалов. Сигнал, приведенный на рисунок 1.14, относится к числу импульсных.

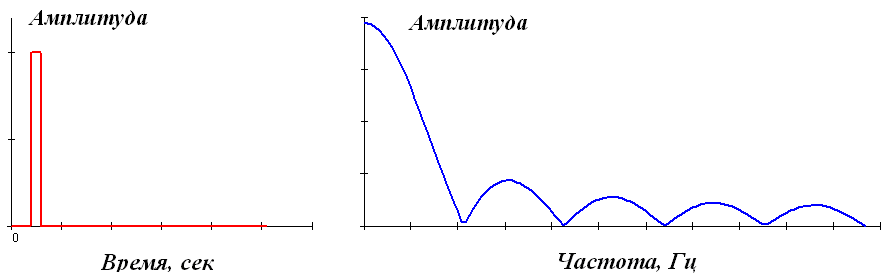
Рисунок. 1.14. Импульсный сигнал и модуль его спектра.