МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ХАРКІВСЬКИЙ

КОМПЬЮТОРНО-ТЕХНОЛОГІЧНИЙ КОЛЛЕДЖ

НАЦІОНАЛЬНОГО ТЕХНІЧНОГО УНІВЕРСИТЕТУ

«ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ УНІВЕРСИТЕТ»

Стислий довідник з предмету

„ Математичний аналіз ”

для студентів 2 курсу навчання.

2011-2012

ВСТУП

Основна задача предмету «Основи вищої математики» для середніх спеціальних закладів полягає в тому, щоб озброїти студентів основами математичних знань і навичок в обсязі, необхідному для їх повсякденної практичної діяльності, для освоєння загально-технічних і спеціальних предметів, а також для дальшого підвищення кваліфікації шляхом самоосвіти.

Успіх у математиці менше всього залежить від

запам'ятовування великої кількості фактів, окремих формул і т. ін. Хороша пам’ять у математиці, як і у будь – якій іншій справі, є корисною, але ніякої особливої виняткової пам’яті більшість видатних учених не мала.

Андрій Колмогоров

Комплексні числа

1.1 Означення комплексного числа.

Число, яке задовільняє рівнянню х² = -1 позначимо буквою i та назвемо його уявною одиницею.

Таким чином, i² = -1.

Число вигляду z = a + bi, де a i b дійсні числа,

а і –уявна одиниця, зветься комплексним числом.

При цьому а – дійсна частина комплексного числа,

bi – уявна частина.

Множину комплексних чисел позначають буквою С.

Запис комплексного числа в вигляді z = a + bi називають алгебраїчною формою комплексного числа.

Два комплексних числа z₁ = a + bi і z₂ = c + di звуться рівними тоді і тільки тоді, коли а = с і b = d, тобто коли рівні дійсні частини і коефіцієнти уявних частин.

Поняття «>» або «<» для комплексних чисел не визначаютьcя.

Комплексне число z = 0 + 0i називається нулем і позначається 0, комплексне число z = a + 0i ототожнюється з дійсним числом а , тобто а + 0і = а, комплексне число z = 0 + bi називається числом уявним і позначається bi , тобто 0 + bi = bi.

Число 0 є єдиним числом, яке одноразово відноситься і до дійсних і до уявних чисел.

Комплексні числа a + bi i a – bi називаються спряженими.

1.2 Геометрична інтерпретація (тлумачення) комплексного числа

Нехай дано комплексне число z = a + bi. Поставимо йому у відповідність точку M(a,b) координатної площини або радіус-вектор (a,b).

При цьому координатна площина називається комплексною площиною, вісь абсцис - дійсною віссю, а вісь ординат-уявною віссю.

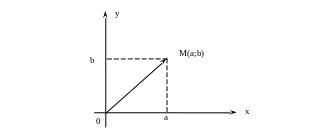
Кожному комплексному числу z = a + bi буде відповідати єдина точка M(a, b) або єдиний вектор (a,b) комплексної площини. І, навпаки, кожній точці комплексної площини відповідає єдине комплексне число z = a + bi.

1.3 Дії над комплексними числами в алгебраїчній формі.

Алгебраїчні дії над комплексними числами зводяться до виконання дій над многочленами:

Додавання. Сумою двох комплексних чисел

z₁= a₁ +b₁i і z₂ = a₂ + b₂i зветься число

z = z₁ + z₂ = ( a₁ + a₂ ) + ( b₁ + b₂) i.

Віднімання. Віднімання вводиться, як операція , обернена додаванню:

z₁ – z₂ = (a₁ + b₁i ) – ( a₂ + b₂ i ) =

( a₁ + b₁i ) + ( -a₂ – b₂i ) = (a₁ – a₂ ) + ( b₁ - b₂ )i

Множення. Добутком двох комплексних чисел

z₁ = a₁ + b₁i і z₂ = a₂ + b₂i називається число

z₁ · z₂ = ( a₁a₂ – b₁b₂) + ( a₁b₂ + a₂b₁)·i.

Замітимо, що добуток двох спряжених чисел дає дійсне число:

( a + bi ) x ( a – bi ) = a² – b² i² = a² + b².

Ділення. Ця дія визначається як обернена до множення. Але ми використовуємо практичний спосіб ділення:

Піднесення комплексного числа до степеня

виконується за формулами піднесення двочлена до степеня, але при цьому треба враховувати, що

i¹ =i і ⁴ⁿ⁺¹ = і

i² =-1 і ⁴ⁿ⁺² = -1

i ³=-і і ⁴ⁿ⁺³ = -і

i⁴ =1 і ⁴ⁿ = 1

Витягування кореня.

знак «+» у дужках, якщо b > 0,

знак «-» у дужках, якщо b < 0.

1.4 Тригонометрична форма комплексного числа.

Нехай дано комплексне число z = a + bi.

Зобразимо його в геометричній формі .

Введемо параметри комплексного числа.

Модулем комплексного числа називається абсолютна величина вектора, який відповідає цьому числу

r =

( на основі теореми Піфагора для ).

Аргументом комплексного числа z≠0 називається величина кута φ між додатнім напрямом дійсної осі 0x і радіус-вектором , який відповідає цьому числу. Для аргумента z = a + bi використовується позначення:

φ=arg z = arg (a+bi), φ = MOX.

Отже, тригонометрична форма комплексного числа має вигляд

z = r (cos φ + i sin φ), де r= ; φ =arctg .

Дії над комплексними числами, заданими в тригонометричній формі

Складання і віднімання комплексних чисел зручніше виконувати в алгебраїчній формі. Для решти операцій зручніша тригонометрична форма.

Множення

Ділення

Піднесення до ступеня

-

формула Муавра.

Витягання кореня -го ступеня

- арифметичний корінь

= 0; 1; 2; … - 1.

Корінь ступеня на множині комплексних чисел має різних значень. Все значення рівні між собою і рівні 0. Все значення кореня -го ступеня

зображаються точками на колі з центром

на початку координат, радіус якої рівний .

Ці точки – вершини правильного -угольника.

1.5 Показникова форма комплексного числа

Вивчаючи функцію y=e для комплексної змінної, Ейлер встановив співвідношення

e^iφ = cosφ + i sinφ ,

яке зветься формулою Ейлера.

З цієї формули витікає, що кожне комплексне число z≠0 можна записати у вигляді

z = r (cosφ +i sinφ)= r · e , яка і зветься показниковою формою комплексного числа.

Числові послідовності, елементарні функції.

2.1 Поняття функції та границі функції в точці та на ∞.

Числовою функцією з областю ви значення D називається залежність, при якій кожному числу x із множини D (області визначення) ставиться у відповідність єдине число y. Записують цю відповідність так: y = f (x).

Область визначення функції f — це множина тих значень, яких може набувати аргумент x. Вона позначається D (f).

Область значень функції f — це множина, яка складається із всіх чисел f (x), де x належить області визначення. Її позначають E (f).

Функція може задаватися не тільки за допомогою формули, а й за допомогою таблиці, графіка чи словесного опису.

Число b называется границею функції f(х) при х добігаючому до а, якщо для будь-якого доволі малого визначеного ε>0 існує таке δ>0, що для усіх х, таких, що |х-а|<δ виконується нерівність |f(x) - b|<ε.

Функція f(x) називається неперервною в точці а, якщо її границя в цій точці співпадає зі значенням функції в цій же точці або lim f(x) = f(a).