1.4. Расчет ускорений методом планов

При расчете ускорений считаем, что кривошип вращается с постоянной угловой скоростью, тогда ускорение точки А кривошипа вычисляется по формуле [1, 3]

а_А = ω₁²r = м/с². (1.4)

Ускорение а_В точки В шатуна связано с ускорением точки А кривошипа зависимостью [1, 3].

→ → → →

а_В = а_А + аⁿ_ВА+ а^τ_АВ , (1.5)

где а_А – переносное ускорение; аⁿ_ВА и а^τ_АВ – нормальная и тангенциальная составляющие относительного ускорения.

Ускорение а_А направлено параллельно кривошипу из точки А к центру О вращения звена, ускорение аⁿ_ВА – параллельно шатуну, а а^τ_АВ – перпендикулярно АВ.

Поскольку в относительном движении шатун вращается, то

аⁿ_ВА = ω₂² =

Ускорение точки В шатуна направлено параллельно направляющей ползуна.

Уравнение (1.5) имеет два неизвестных. Графическое его решение для пятого положения механизма приведено на рис. 5.

Масштабный коэффициент плана ускорений:

Рис. 5

Длина отрезка n₄a₄, которым изображается на плане ускорений aⁿ_BA, вычисляется следующим образом:

n₄a₄ = aⁿ_BA/μ_а = мм.

Ускорение а_S2 центра масс шатуна определяется по свойству подобия плана ускорений. Составляем пропорцию:

Отрезок а₄s₂ откладываем на плане ускорений на отрезке а₄b₄ от точки а₄. Полученную точку s₂ соединяем с полюсом p_a плана. Отрезок s₂p_a изображает в масштабе μ_а ускорение центра масс шатуна.

Расчет ускорений:

а^τ_BA = n₄b₄∙μ_a = = м/с²;

a_BA = a₄b₄∙μ_a = = м/с²;

a_B = p_ab₄∙μ_a = = м/с²;

a_S2 = p_as₂∙μ_a = = м/с².

Расчет углового ускорения шатуна:

= = 1/с².

Расчет ускорений выполнен для двух положений механизма. Результаты приведены в табл. 2.

Таблица 2

Ускоре-ние № п/п	aA	anBA	aτBA	aBA	aS2	aB	ε2
	м/с2						1/с2

1.5. Кинематический анализ механизма методом диаграмм

1.5.1. Построение диаграммы перемещения выходного звена

Диаграмма перемещения выходного звена строится в зависимости от функции времени. При ω₁ = const каждому моменту времени соответствует определенный угол поворота кривошипа. В связи с этим по оси абсцисс откладывают не только время, но и угол α поворота кривошипа, которому соответствует определенное его положение.

На оси абсцисс диаграммы (рис. 6) откладываем отрезок 0 – 12 длиной ℓ=180 (или 240) мм. Он изображает в масштабе μ_α угол поворота кривошипа, равный 360⁰ или 2π. Тогда масштабный коэффициент μ_α будет вычисляться по формуле:

=

Если угол измеряется в радианах, то

=

Отрезок ℓ изображает и время t_ц одного полного оборота кривошипа. Его можно вычислить следующим образом:

Тогда масштабный коэффициент = с/мм.

Масштабный коэффициент μ_s оси ординат примем равным μ_ℓ (масштабный коэффициент разметки).

μ_s =

Для построения диаграммы перемещения (рис. 6) определим длину отрезка , который в масштабе μ_α изображает угол рабочего хода (угол между крайними положениями кривошипа во время рабочего хода механизма).

= = мм.

Отрезок отложим на оси абсцисс диаграммы от начала координат. Этот отрезок разделим на шесть равных частей и обозначим соответствующие положения механизма (0; 1; 2; 3; 4; 5; 6). Оставшийся отрезок разделим на 6 равных частей и обозначим соответствующие холостому ходу положения механизма. Это – 7, 8, 9, 10, 11 и 12 положения.

Из точек 1, 2, 3 ….. 12 оси абсцисс диаграммы проводим к ней перпендикуляры, на которых откладываем отрезки В₀В₁, В₀В₂, В₀В₃ и т.д., изображающие перемещение ползуна в 1-м, 2-м, 3-м и т.д. положениях механизма. Полученные точки соединим плавной кривой. Это и есть диаграмма перемещения.

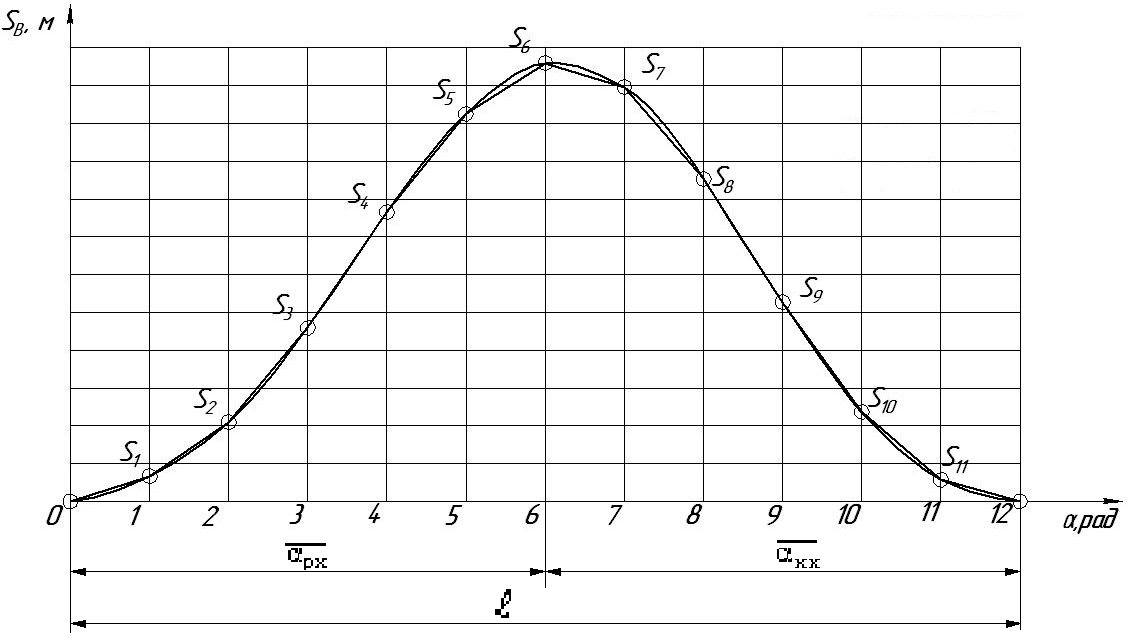
Рис. 6. График перемещения точки В