
- •Электротехника
- •Содержание
- •Методы расчета электрических цепей постоянного тока ..............5
- •Расчет электрических цепей переменного тока………………….16
- •2.1. Общие положения………………………………………………..16
- •2.5. Задание для самостоятельного расчета схемы
- •Расчет динамических режимов линейных электрических
- •3.1. Общие положения…………………………………………...…..32
- •Введение
- •Методы расчета электрических цепей постоянного тока
- •1.1 Общие положения
- •Метод узловых потенциалов
- •Метод контурных токов
- •Метод эквивалентного генератора
- •Варианты заданий для самостоятельного решения
- •Расчет электрических цепей переменного тока
- •2.1 Общие положения
- •2.2 Методика расчета электрической цепи с одним источником эдс путем эквивалентного преобразования схемы.
- •Задание для самостоятельного расчета схемы с последовательным соединением элементов
- •Задание для самостоятельного расчета схемы с одним источником эдс при смешанном соединении элементов
- •Задание для самостоятельного расчета схемы с несколькими источниками
- •Методические указания и задание для самостоятельного расчета трехфазной цепи
- •Расчет динамических режимов линейных электрических цепей
- •3.1 Общие положения
- •3.2 Методика расчета переходного процесса в линейной электрической цепи классическим методом.
- •3.3. Задание для самостоятельного расчета переходного процесса классическим методом.
- •Список рекомендуемой литературы
- •350072, Г. Краснодар, ул. Московская, 2, кор. А
Метод узловых потенциалов
Подписать узлы, расставить произвольно направления токов в ветвях и подписать токи.
Заземлить один любой узел, т.е. принять его потенциал за «0».
Для всех незаземленных узлов составим уравнения по 1-му закону Кирхгофа.
В полученной системе уравнений число искомых токов больше числа уравнений, поэтому выполняем замену переменной, а именно, выражаем искомые токи через потенциалы незаземленных узлов.
*Все
токи ветвей представляем выражениями
вида ![]() ,
,
где Uab – напряжение ветви, между узлами «a» и «b» которой течет ток I, причем ток направлен от узла «a» к узлу «b», в противном случае указываем напряжение Uba;
±∑E – алгебраическая сумма ЭДС ветви ab, в которой ЭДС учитывается со знаком «+», если ток I и ЭДС сонаправлены;
Rab – полное сопротивление ветви ab.
Подставляем выражения п.1.3.4. в уравнения п.1.3.3., подставляем исходные данные, решаем систему и находим потенциалы незаземленных узлов.
Используя выражения п.1.3.4. находим искомые токи ветвей.
Проверяем полученные результаты, например, по балансу мощности.
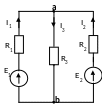
Пример расчета методом узловых потенциалов |
|
выполняем п. 1.3.1 |
выполняем п. 1.3.2 |
|
φb=0 |
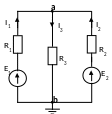
выполняем п. 1.3.3 |
|
Т
|
|
выполняем п. 1.3.4 |
|
|
|
выполняем п. 1.3.5 |
|
Подставляем выражения п.1.3.4. в уравнения п.1.3.3., получим:
подставляем
исходные данные, решаем систему (в
рассматриваемом примере система
содержит одно уравнение) любым мат.
методом и находим потенциалы
незаземленных узлов (в данном случае
находим |
|
выполняем п. 1.3.6 |
|
Используя выражения п.1.3.4, после выполнения п.1.3.5, можно найти искомые токи ветвей I1, I2, I3. |
|
выполняем п. 1.3.7 |
|
Составим баланс мощностей для схемы п. 1.3.1
Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно. |
|
Метод контурных токов
Подписать узлы, расставить произвольно направления токов в ветвях и подписать токи.
Определить независимые контуры и произвольно выбрать их направления обхода.
Для всех независимых контуров составим уравнения по 2-му закону Кирхгофа.
В полученной системе уравнений число искомых токов больше числа уравнений, поэтому выполняем замену переменной, а именно, выражаем искомые токи ветвей через контурные токи.
*Все токи ветвей представляем выражениями вида
![]() ,
,
где
![]() – ток i-ой
ветви;
– ток i-ой
ветви;
![]() – контурный ток 1-го, 2-го, 3-го и т.д.
контуров в которые входит рассматриваемая
ветвь. Если ток ветви Ii
и контурный ток Ik
сонаправлены, то учитывается знак «+».
– контурный ток 1-го, 2-го, 3-го и т.д.
контуров в которые входит рассматриваемая
ветвь. Если ток ветви Ii
и контурный ток Ik
сонаправлены, то учитывается знак «+».
Подставляем выражения п.1.4.4. в уравнения п.1.4.3., подставляем исходные данные, решаем систему и находим контурные токи.
Используя выражения п.1.4.4. находим искомые токи ветвей.
Проверяем полученные результаты, например, по балансу мощности.
Пример расчета методом контурных токов |
|
выполняем п. 1.4.1 |
выполняем п. 1.4.2 |
|
|
выполняем п. 1.4.3 |
|
Составим уравнения по второму закону Кирхгофа для независимых контуров:
контур
1 -
контур
2 -
|
|
выполняем п. 1.4.4 |
|
У
|
|
выполняем п. 1.4.5 |
|
Подставляем выражения п.1.4.4. в уравнения п.1.4.3., получим:
Подставляем исходные данные, решаем систему любым мат. методом и находим контурные токи Ik1, Ik2, Ik3. |
|
выполняем п. 1.4.6 |
|
Используя выражения п.1.4.4., можно найти искомые токи ветвей I1, I2, I3. |
|
выполняем п. 1.4.7 |
|
Составим баланс мощностей для схемы п. 1.4.1
Подставляем известные и расчитанные величины в правую и левую части баланса, если равенство выполняется, то задача решена верно. |
|

 .к.
незаземлен лишь узел «а», то необходимо
составить только одно уравнение
.к.
незаземлен лишь узел «а», то необходимо
составить только одно уравнение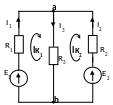 кажем
контурные токи на схеме и выразим токи
ветвей через контурные токи:
кажем
контурные токи на схеме и выразим токи
ветвей через контурные токи: