ЛАБОРАТОРНАЯ РАБОТА 1

ДИСКРЕТНЫЙ ВАРИОЦИОННЫЙ РЯД

Цель работы:

Изучение основных характеристик дискретного вариационного ряда, вычисление их с помощью формул и встроенных функций MS Excl; копирование формул, использование абсолютных и относительных ссылок, имен ячеек. Применение различных способов форматирования ячеек таблицы, построение диаграмм.

Задание

Для заданного дискретного распределения найти выборочные характеристики: выборочную среднюю, выборочные и «исправленные» дисперсии и среднеквадратическое отклонение, моду, медиану и коэффициент вариации. Построить графические изображения вариационного ряда. Работу сохранить в своей папке под именем «Дискретное распределение».

Дискретное распределение. В результате обследования 70 свиноматок, по количеству родившихся поросят в одном помете, получено распределение, приведено в таблице 1.

Таблица 1

xi	4	5	6	7	8	9	10	11	12
ni	3	4	6	11	15	14	8	7	2

где: x_i признак( количество поросят в одном помете); n_i - частота появления признака (у скольких свиноматок проявился признак).

Порядок выполнение работы

1. Оформить заголовки таблицы как показано на рисунке 1.

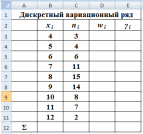
рис. 1

С помощью команды Формат/Ячейки/ Выравнивание можно выбрать нужный режим вертикального и горизонтального выравнивания; осуществить объединение ячеек, перенос слов и т.п.

Командой Формат/Ячейки/Шрифт устанавливаются различные виды шрифтов и оформляются индексы (предварительно нужный символ необходимо выделить комбинацией клавиши Shift и стрелка).

Для вставки символов греческого алфавита применяем команды Вставка/ Символ.

Чтобы выделить несколько ячеек, щелкнем по одной из них, а затем, при нажатой левой кнопке мыши, переместимся по всему диапазону (курсор имеет вид жирного белого креста), весь диапазон оказывается в черной рамке. Теперь эти ячейки можно объединить, скопировать, переместить и т.п. для объединения нескольких ячеек можно применить кнопку панели инструментов (Объединить и поместить в центре).

Когда курсор принимает форму тоненького крестика с двунаправленными стрелками, содержимое выделенных ячеек можно перемещать.

Ширину столбцов (высоту строк) можно изменить с помощью мыши, наведя ее указатель на область заголовков столбцов (строк) и, когда он примет вид двунаправленной стрелки, произвести нужно действие.

2. Найдем объем выборки (сумму всех частот).

Чтобы произвести вычисления, в ячейке необходимо внести формулу. Формула начинается со знака =, в выражении формулы могут быть знаки арифметических действий, скобки, числа, адреса и имена ячеек, а также встроенные функции. Для нахождения суммы всех частот (объема выборки) в ячейку C12 запишем формулу: =СУММ(C3:C11) и нажмем клавишу Enter. В ячейке появится результат, равный 70.

Если вместо результата появилось сообщение об ошибке, проверьте раскладку клавиатуры (EN), так как адреса ячеек маркируются буквами английского алфавита.

Нахождение суммы, а также среднего, наибольшего и наименьшего значений ряда можно осуществить иначе, если воспользоваться кнопкой Ʃ (Статистические функции). Любую функцию можно выбрать, если воспользоваться услугами Мастера функций, доступ к которому осуществляется кнопкой f_x (около Строки формул). Если содержимое формулы подлежит исправлению, это можно осуществить, поместив курсор в Строку формул. После корректировки нажать кнопку Готово или клавишу Enter.

3. Отношение соответствующих частот к объему совокупности (выборки) называются относительными частотами (частностями).

Относительные частоты 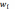найдем по формуле:

,

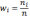где n -объем выборки.

В ячейку D3 внесем формулу: =C3/$C$12. В этой формуле на ячейку C3 - относительная, а на ячейку С12 - абсолютная.

Формулу можно набирать не только с клавиатуры, но и с помощью мыши, а именно:

• установили курсор в ячейку D3;

• нажали клавишу =;

• щелкнули мышью по ячейке С3 (в строке формул появилось соответствующая запись);

• нажали клавишу /;

• щелкнули мышью по ячейке С12 и нажали клавишу F4;

• Enter.

Теперь формулу из ячейки D3 необходимо скопировать в ячейки D4:D11. Для этого:

• щелкнем по ячейке D3 (теперь она выделена черной рамочкой, т.е. стала активной);

• перемещаем курсор в правый нижний угол этой рамочки, что бы курсор принял вид тоненького черного креста;

• нажимаем левую кнопку мыши и перемещаемся вниз, до ячейки D11 (весь диапазон D3:D11 оказывается в серой рамке);

• отпускаем кнопку мыши (в ячейках появились результаты).

Теперь посмотрите, какие формулы оказались в ячейках диапазона D3:D11 и ответьте на вопрос, для чего нужны абсолютные и относительные ссылки?

4. Накопленной частотой γ_i (относительной накопленной частотой) называется сумма всех часто (относительных частот) вариационного ряда, предшествующих данному признаку с частотой (относительной частотой) этого признака. Накопленную частоту можно найти по формуле:

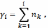
Накопленную относительно частоту можно будет найти, разделив накопленную частоту на объем совокупности n.

Для вычисления накопленных частот в ячейку Е3 внесем формулу :=СУММ($C$3:C3) и скопируем ее в диапазон Е4:Е11.

5. Скопируем из ячейки С12 формулу в ячейку D12.

6. Геометрическая иллюстрация статистических данных придаёт им наглядность. Применяется несколько способов графического изображения рядов распределений в зависимости от вида и поставленной задачи: полигон, гистограмма, кумулятивная кривая (кумулята), огива.

Полигоном частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (x₂, n₂), … (x_k, n_k), где x_j- варианты выборки, w_j- соответствующие им относительные частоты.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x₁, n₁), (x₂, n₂), … (x_k, n_k), где x_j -варианты выборки, w_j-соответствующие им частоты.

Гистограмма обычно строится для непрерывно варьирующего признака, рассмотрим её позднее.

Кумулятивной кривой (кумулятой) называют ломаную, отрезки которой соединяют точки (x₁, y₁), (x₂, y₂), … (x_k, n_k), где x_j- варианты выборки, y₁- соответствующие им накопленные частоты.

Если на горизонтальной оси откладывать накопленные относительные частоты, а на вертикальной - значения признака, то полученная кривая носит название огивы. Таким образом, принципиальных различий между кумулятой и огивой нет, оба графика выполняют одинаковые функции.

Для построения полигона частот выделим диапазон ячеек (прямоугольную область) B2:C11, в котором расположены значения признака и соответствующие им частоты. Находим на панели инструментов Мастера диаграмм или в меню Вставка соответствующую опцию. Выбираем точечную диаграмму. Изменяя объекты диаграммы (для этого можно использовать контекстное меню, вызываемое правой кнопкой мыши), приводим её к соответствующему виду (рисунок 2).

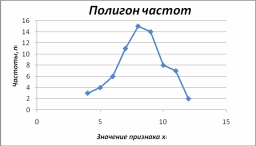
Рис.2

При построении полигона относительных частот (Рисунок 4) выделяем несмежные диапазоны B2:B11и D2:D11. Для этогоудерживаем нажатой клавишу Ctrl. При построении кумуляты поступаем аналогично.