4.2. Распределение напряжений в грунте от действия равномерной нагрузки

В реальных условиях эксплуатации инженерных объектов транспорта и хра-нения нефти и газа очень часто фундаменты передают на грунт не сосредото­ченную, а сплошную нагрузку. Рассмотрим, как определяются напряжения в толще основания, если на абсолютно жесткий сплошной прямоугольный в плане фундамент действует равномерно распределенная нагрузка q.

Для определения напряже­ний в грунте под фундаментом можно воспользо­ваться формулой (4.9). Причем существует два метода решения такой задачи: приближенный и точный.

4.2.1. Приближенный способ определения напряжений в грунте

состоит в том, что площадь фундамента разбивают на ряд малых площадок и нагрузку, действующую на каждую из них, принимают за сосредоточенную силу, прило­женную в центре тяжести площадки (рис. 4.5). И чем больше число i элементарных площадок разбиения, тем точнее результаты расчета. Поэтому для практической реализации алгоритма расчета рекомендуется использовать ПЭВМ.

Тогда суммарное напряжение в точке т будет равно

(4.11)

где значения К_i в каждом случае вычисляют в зависимости от отношения r_i/z.

y

q

z

m

P₁

P₂

r₁

r₂

a

I

II

m

P₃

r₃

r₄

a

P₄

III

IV

b

b

Рис. 4.5. Схема определения напряжения _Z в произвольной точке m массива грунта при действии на фундамент равномерно распределенной нагрузки q

4.2.2. Более точный метод определения напряжений в грунте

Более точное решение задачи по определению напряжения _Z в произволь­ной точке m массива грунта при действии на основание фундамента равно­мерно распределенной нагрузки q было получено А. Лявом [12]. Оно состоит в том, что искомые напряжения в грунте определяют интегрированием напряже­ний, возникающих от элементарных сосредоточенных сил, расположенных на загруженной фундаментом площадке.

Для всех составляющих напряжений в грунте ( ) соответст­вующие выражения были опубликованы в работе В.Г. Короткина [10]. В частности, при действии равномерно распределенной нагрузки со сто­роны подошвы прямоугольного в плане фундамента (рис. 4.6) выделяют беско­нечно малый элемент загруженной площади и, считая нагрузку на этот элемент сосредоточенной, пользуясь формулой (4.9), путем интегрирования по всей за­груженной площади получают все компоненты напряженного состояния грунта в произвольной точке его массива.

Таким образом, из решения (4.9) для сосредоточенной силы путем замены в нем (рис. 4.6) силы Р на и интегрирования в пределах от – а до + а и от – b до + b получим:

q

x

x

a

a

z

x

b

b



m(x, y, z)



y

Рис. 4.6. Расчетная схема для определения компонентов напряжений в грунте от действия равномерно распределенной нагрузки со стороны подошвы фунда­мента

Для точек, расположенных по вертикали, проходящей через центр площади загружения, то есть при x = y = 0 выражение для _Z принимает вид:

(4.13)

В аналогичном виде могут быть написаны и все остальные состав­ляющие. Выражения для них не приводятся вследствие большой сложности. В случае необходимости они могут быть найдены в указан­ной работе В. Г. Короткина.

Из рассмотрения приведенных выше формул нетрудно убедиться, что на­пряжения _Z, по оси площади загружения равны учетверенным зна­чениям на­пряжений _Z в соответствующих точках, расположенных на удвоенной глубине на вертикалях, проходящих через углы площади загружения.

Рассмотрим практические решения задач по данной тематике.

Задача. 4.1. Построить эпюры напряжений в грунте от действия сосредото­ченной силы Р =100 т, приложенной к его поверхности. Исследова­ние характера и величины изменения напряжений в продольном направлении грунта, т.е. по его глубине, произвести под точкой приложения силы Р, когда r = 0, а в поперечном направлении - на глубине z = 3 м (рис.4.7).

x

x

P

P

s_z

y

y

z

r

z

Рис.4.7. К определению напряжений в произвольной точке массива грунта

Напряжение в произвольной точке грунта, действующее параллельно при­ло­женной силе Р, определяется по формуле:

Ввиду громоздкости вычислений для определения законов изменения на­пряжений в грунте под точкой приложения силы Р (рис.4.8) и в поперечном направлении на глубине z = 3 м (рис.4.9) воспользуемся стандартной програм­мой MATHCAD –7.

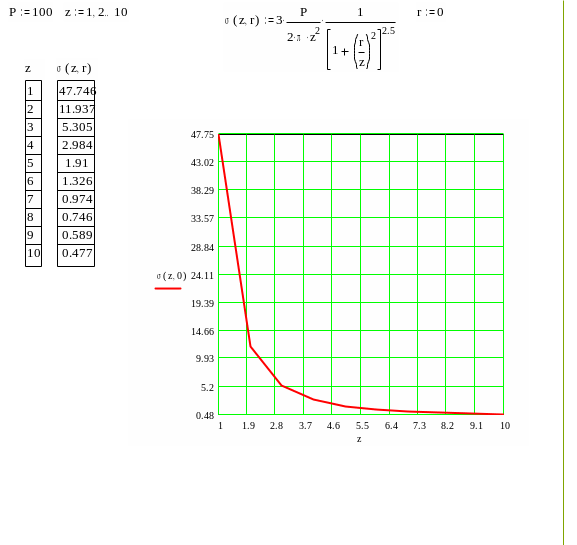
Рис.4.8. Функция s_z (z,r=0)

На рис. 4.8 и 4.9 параметры z и r имеют размерность м, а функция s_z – Т/м².

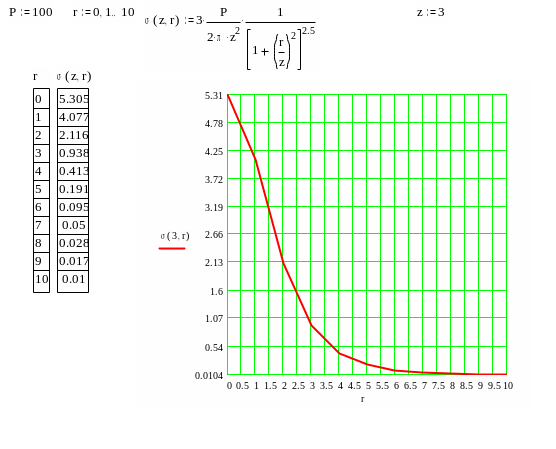
Рис.4.9. Функция s_z (z=3,r)

Задача 4.2. Определить характер осадки поверхности основания при воздей­ствии на него сосредоточенной силы Р =100 т.

Решение

Осадка основания в произвольной точке массива грунта определяется сле­дующим выражением:

где Е и m - соответственно модуль общей деформации и коэффициент Пуас­сона грунта.

На поверхности основания z = 0, поэтому её осадка равна:

Из последней зависимости видно, что осадка поверхности основания от точки приложения силы Р меняется по линейному закону.

Если, например, грунт основания состоит из мелкого маловлажного песка, то Е = 2500 Н/см², m = 0,3 и на расстоянии r =10 м от точки приложения нагрузки осадка поверхности основания составит

Задача 4.3. Определить величину напряжения s_Z в произвольной точке m массива грунта, расположенной на глубине 10 м и на расстоянии 5 м от края фундамента (рис. 4.5) при действии равномерно распределенной нагрузки q = 166,7 кН/м², если а =3 м, в = 2 м.

Решение

Разбиваем всю поверхность прямоугольного в плане фундамента на четыре прямоугольных участка площадью f = a×b, как показано на рис.4.5 (причем, чем больше число элементарных площадок разбиения i, тем точнее будут резуль­таты расчёта) и в центре каждой площадки прикладываем сосредоточенные силы Р₁ = Р₂ = Р₃ = Р₄ = = 1000 кН.

Все дальнейшие вычисления сведены в таблицу 4.1.

Таблица 4.1

№ уча­стка	Pi , кН	ri , м	ri /z	Ki	, кН/м2	кН/м2
I	1000	8,3	0,83	0,13	10	1,3
II	1000	6,4	0,64	0,20	10	2,0
III	1000	8,3	0,83	0,13	10	1,3
IV	1000	6,4	0,64	0,20	10	2,0

Всего s_Z = 6,6 кН/м²

Таким образом, в произвольной точке m массива грунта, расположенной на глубине 10 м и на расстоянии 5 м от края фундамента действуют вертикальные сжимающие напряжения s_Z = 6,6 кН/м² .