3.3. Коэффициент бокового давления и расширения грунта

Грунт, который испытывается в компрессионном приборе под действием вертикальной нагрузки , деформируется только в на­правлении оси z (рис. 3.4).

_z = 

_x = 

0

_y = 

x

z

_z = 

y

Рис. 3.4. Схема обжатия грунта в компрессионном приборе.

Боковые деформации в направлении осей х и у равны нулю, так как стенки прибора обладают большой жесткостью.

Если обозначить нормальные напряжения в скелете грунта, параллельные оси z, через _z, а параллельные осям х и у - через _x и _y для условий сжатия в компрессионном приборе, то можно написать

(3.2)

где  - коэффициент бокового давления.

Этот коэффициент представляет собой отношение поперечных сжимающих напряжений к продольным, т. е

(3.3)

В теории сыпучих тел установлено, что для песков (сыпучих тел), находя­щихся в состоянии предельного равновесия, величину  можно вычислить по формуле

(3.4)

где  - угол внутреннего трения грунта.

Лабораторное определение коэффициента бокового давления, как для сыпу­чих, так и для связных грунтов может быть произве­дено на приборе трехосного сжатия - стабилометре, схема которого приведена на рис. 3.5.

Устанавливая образец 12, заключенный в тонкую резиновую оболочку, в при­бор, можно, загружая поршень 11 силой Р, создать любое предельное сжатие образца интенсивностью ₁. Нагнетая же через трубку 12 в замкнутую камеру 15 воздух или жидкость, можно создать любое боковое сжатие образца интен­сивностью ₂,.

В процессе испытания можно так подобрать напряжения ₁ и ₂, что боко­вые деформации _x, и _y будут равны нулю. Тогда соот­ношение опреде­ляет величину коэффициента бокового давления.

По данным ряда исследователей, для песков  = 0,40 - 0,42, а для глин  = 0,70 - 0,75.

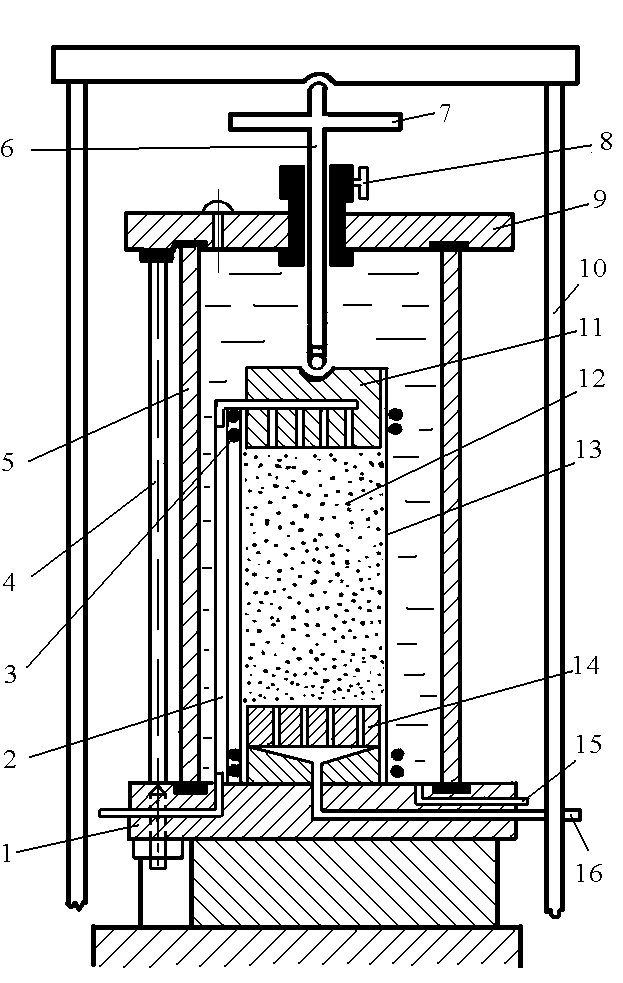
1 - база прибора; 2 - верхняя дре­нажная трубка; 3 - резиновые ман­жеты; 4 - стяжной болт; 5 - стенка прозрачного цилиндра; 6 - шток; 7 - диск штока; 8 - стопорный винт; 9 - крышка прибора; 10 — тяга гру­зовой рамы; 11 - подвижный пор­шень; 12 - образец грунта; 13 - ре­зиновая оболочка; 14 - неподвижный поршень; 15 - трубка для подачи во­ды; 16 - нижняя дренажная трубка.

Рис. 3.5 Схематический разрез стабилометра типа ДИИТ.

В грунтах зависимость между напряжениями и полными де­формациями мо­жет быть принята линейной в форме  = E (за­кон Гука).

В случае трехосного напряженного состояния полную дефор­мацию грунта в направлении какой-либо оси, например _X, можно представить в виде

(3.5)

где  - коэффициент Пуассона грунта, т. е. отношение поперечной относи­тельной деформации (сжатия) к продольной отно­сительной деформации.

Значение  может быть выражено через коэффициент бокового давления . Вследствие того что  определяет соотношение глав­ных напряжений в усло­виях отсутствия боковых деформаций зависимость (3.5) принимает следующий вид:

(3.6)

Принимая во внимание, что и подставляя в (3.6), получим

(3.7)

Из зависимости (3.7) можно получить значение коэффициента бокового дав­ления

(3.8)

Учитывая значения  для соответствующих грунтов, по (3.7) вычислены сле­дующие значения :

Грунт		Грунт	
Песок утрамбо­ванный	0,265	Суглинок	0,38-0,4
Песок рыхлый	0,296	Глина	0,41-0,43

Для изотропных тел  = 0,25, для стали;  = 0,30, для резины  = 0,50.

Таким образом, оказывается, что  для грунтов имеет прибли­зительно те же значения, что и для твердых тел.