Аналитическое выражение переходной функции.
Передаточная функция замкнутой системы:
>> S=tf('p');
>> W=(125*(0.02*S+1))/(S*(0.125*S+1)*((0.005^2)*(S^2)+0.002*S+1));
>> H=(0.04*(S^2))/(0.2*S+1);
>> sys3=1/(1/W+H+1);
>> sys4=sys3/S;
0.5 p^2 + 27.5 p + 125
-------------------------------------------------------------------------------------------------
6.25e-007 p^6 + 5.813e-005 p^5 + 0.1257 p^4 + 5.827 p^3 + 28.5 p^2 + 125 p
С помощью программы Matlab найдем аналитическое выражение переходной
функции системы. При использовании команды:
>> [R,P,K]=residue(num,den),
где результатом выполнения этой команды будут векторы-столбцы вычетов R и полюсов Р. Так как у нас комплексно-сопряженные полюса и вычеты, то такую пару слагаемых объединим:
Общая формула:
>> num=[0.5, 27.5, 125]
>> den=[6.25e-007, 5.813e-005, 0.1257, 5.827, 28.5, 125, 0]
>> [R,P,K]=residue(num,den)
R =
0.0006 + 0.0045i
0.0006 - 0.0045i
0.0181
-0.5096 - 0.2699i
-0.5096 + 0.2699i
1.0000
P =
1.0e+002 *
-0.2308 + 4.4519i
-0.2308 - 4.4519i
-0.4197
-0.0245 + 0.0424i
-0.0245 - 0.0424i
0
1)
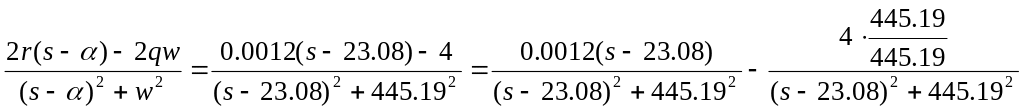
Где оригинал:
2)
Оригинал:
3)
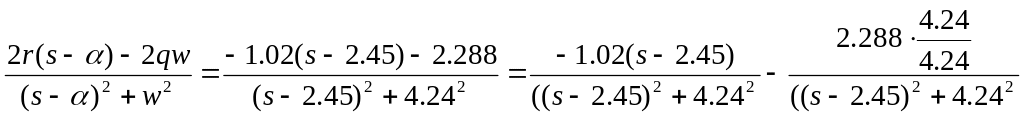
Где оригинал:
.
4)
Оригинал:
Переходная функция:
Выделим составляющую найденной функции, соответствующую доминирующим полюсам:
y1(t)=-
И определим ее график:
Код программы:
>> T=0:0.001:2.5
>> y1=-1.02*exp(-2.45*T).*cos(-4.24*T)-0.54*exp(-2.45*T).*sin(-4.24*T)
>> h=1-1.02*exp(-2.45*T).*cos(-4.24*T)-0.54*exp(-2.45*T).*sin(-4.24*T)+0.0012*exp(-23.08*T).*cos(-445.19*T)-0.009*exp(-23.08*T).*sin(-445.19*T)+0.009*exp(-23.08*T)
>> plot(T,y1,T,h),grid
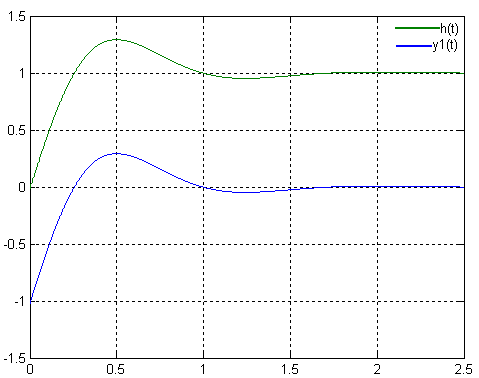
Рис.6
3.6 Амплитудные характеристики замкнутой системы.
Передаточная функция замкнутой системы:
С помощью пакета Matlab:
>> S=tf('p');
>> W=(125*(0.02*S+1))/(S*(0.125*S+1)*((0.005^2)*(S^2)+0.002*S+1));
>> H=(0.04*(S^2))/(0.2*S+1);
>> sys3=1/((1/W)+H+1);
>> bode(sys3)
Показатель колебательности:
Резонансная частота:
.
Полоса пропускания:
.
.
Частота среза:
.
.
Время регулирования:
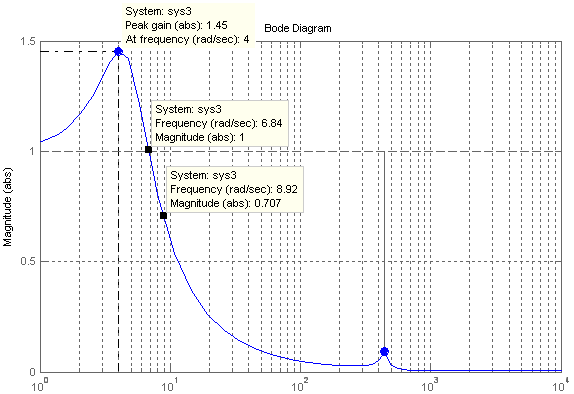
Рис.8
Уравнения состояния и выхода замкнутой системы.
А) Передаточная функция замкнутой системы:
Уравнение состояния и выхода имеют вид:
Составим систему для нахождения
коэффициентов
Используя Матлаб:
>>A=[240000000 4560000 9323200 201120 93.008 1;
4560000 9323200 201120 93.008 1 0;
9323200 201120 93.008 1 0 0;
201120 93.008 1 0 0 0;
93.008 1 0 0 0 0;
1 0 0 0 0 0]
>>B=[240000000; 44000000; 800000;0;0;0]
>>C=inv(A)*B
Отсюда найденные коэффициенты:
Теперь составим уравнение состояния и выхода для нашей системы:
Б) Наблюдаемость и управляемость:
Для проверки свойств управляемости и наблюдаемости этих вариантов, воспользуемся пакетом Matlab:
Код программы:
>>A1=[0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0;
0 0 0 0 1;
-2400000 -4560000 -9323200 -201120 -93.008]
>>B1=[0;0;0;-3e+007;-1.5783e+011]
>>C1=[1 0 0 0 0]
>>K=[B1 A1*B1 A1^2*B1 A1^3*B1 A1^4*B1]
>>rank(K)
>>G=[C1;C1*A1;C1*A1^2;C1*A1^3;C1*A1^4]
>>rank(G)
K =
1.0e+021 *
0 0 0 -0.0000 -0.0000
0 0 -0.0000 -0.0000 0.0000
0 -0.0000 -0.0000 0.0000 0.0000
-0.0000 -0.0000 0.0000 0.0000 -0.0055
-0.0000 0.0000 0.0000 -0.0055 -5.7344
ans = 3
G =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
ans = 5
Если ранг K=n , то система вполне управляемая;
Если ранг G=n , то система вполне наблюдаемая.
Но у нас выполняется только второе условие, следовательно, наша система неуправляемая, но наблюдаемая.