3.2. Заключение об устойчивости системы.

По критерию Найквиста, для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы ЛФЧХ разомкнутой системы в области частот, где ЛАЧХ положительна, принимала значение -180˚ четное число раз или не принимала этого значения, следовательно, данная система устойчива, т.к. ЛФЧХ не принимала значение ни разу в области частот, где ЛАЧХ положительна.

Используя функцию

>>sys1=1/(1/W+H);

>> [mg, fg]=margin(sys1)

в пакете Matlab определим:

-запас устойчивости по фазе

fg =51.0921:

-запас устойчивости по амплитуде:

mg =12.4160

20*lg(g) =20*lg(12.4160)=21.8796,

Запас устойчивости по фазе определяется на частоте, при которой ЛАЧХ принимает значение 0.

Запас устойчивости по амплитуде определяется на частоте, при которой ФЧХ принимает значение -180˚.

Построим ЛАЧХ и ЛФЧХ разомкнутой системы, используя Matlab (bode(u)):

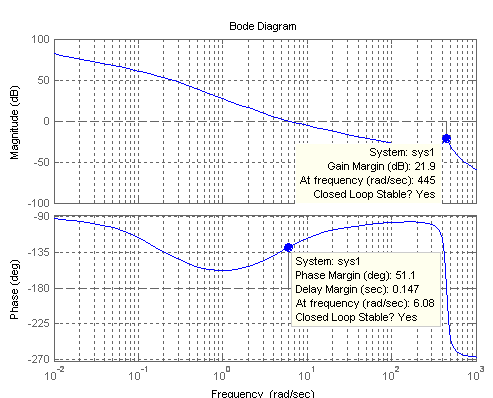
Рис.3

3.3. Показатели качества замкнутой системы.

Нулями передаточной функции называются корни полинома числителя, а полюсами называются корни полинома знаменателя. Вычислим нули и полюса с помощью пакета Matlab:

Определим передаточную функцию замкнутой системы:

>> S=tf('p');

>> W=(125*(0.02*S+1))/(S*(0.125*S+1)*((0.005^2)*(S^2)+0.002*S+1));

>> H=(0.04*(S^2))/(0.2*S+1);

>> sys2=1/(1/W+H+1);

0.5 p^2 + 27.5 p + 125

--------------------------------------------------------------------------------------------

6.25e-007 p^5 + 5.813e-005 p^4 + 0.1257 p^3 + 5.827 p^2 + 28.5 p + 125

>> pole(sys2)

ans =

1.0e+002 *

-0.2307 + 4.4515i

-0.2307 - 4.4515i

-0.4197

-0.0245 + 0.0424i

-0.0245 - 0.0424i

>> zero(sys2)

ans =

-50

-5

Система устойчива, т.к. все полюса находятся в левой полуплоскости.

Показатели качества:

1. Степень устойчивости.

Она характеризует быстродействие системы и равна абсолютному значению вещественной части ближайшего полюса, т.е. η = |Re|=2.45.

2. Время регулирования.

c;

3. Степень колебательности.

.

4. Переходная и импульсная переходная функции.

Передаточная функция замкнутой системы:

Построим графики переходных функций во временных осях, используя пакет Matlab и команды step(sys3) и impulse(sys3).

Код программы:

>> t=0:0.001:2.5

>> S=tf('p');

>> W=(125*(0.02*S+1))/(S*(0.125*S+1)*((0.005^2)*(S^2)+0.002*S+1));

>> H=(0.04*(S^2))/(0.2*S+1);

>> sys3=1/(1/W+H+1);

>> step(sys3,t)

>>impulse(sys3,t)

Показатели качества переходного процесса:

Апериодическая функция - т.к. 1 максимум.

- время, когда впервые достигается

-время достижения максимума.

Время регулирования:

| h(t) – h_уст| < Δ, при t > t_p, Δ = 0,03 h_уст, тогда t_p =1,46 с

Перерегулирование:

Частота колебаний:

ω = 2π / Т = 2·3,14/1,474 = 4,26 1/с

n – число колебаний за время регулирования =1.

Импульсная переходная функция

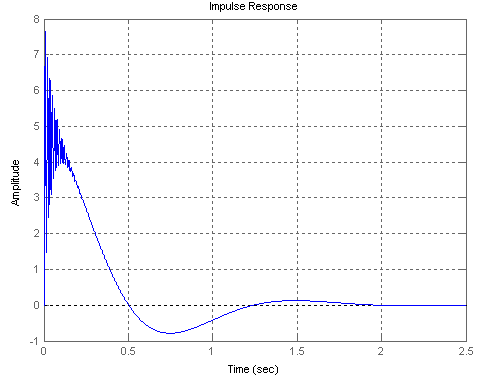
Рис.4

Переходная функция

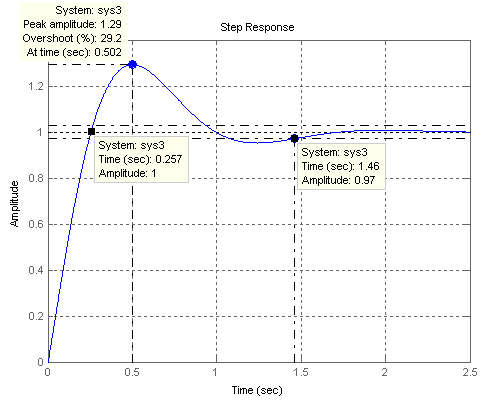
Рис.5