Построить логарифмическую амплитудно-частотную характеристику замкнутой системы, определить полосу пропускания системы, резонансную частоту, показатель колебательности:
Передаточная функция замкнутой системы:
Построим логарифмическую амплитудно-частотную характеристику замкнутой системы, используя программу Матлаб:
>>s=tf('s');
>>w=(250*(0.1*s+1))/(s*(0.75*s+1)*(0.000441*s^2+0.0105*s+1))
>>h=(0.14*s^2)/(0.26*s+1)
>>u=w/(1+w*h)
>>ui=1/((1/w)+h+1)
>>bode(ui)
Показатель колебательности:
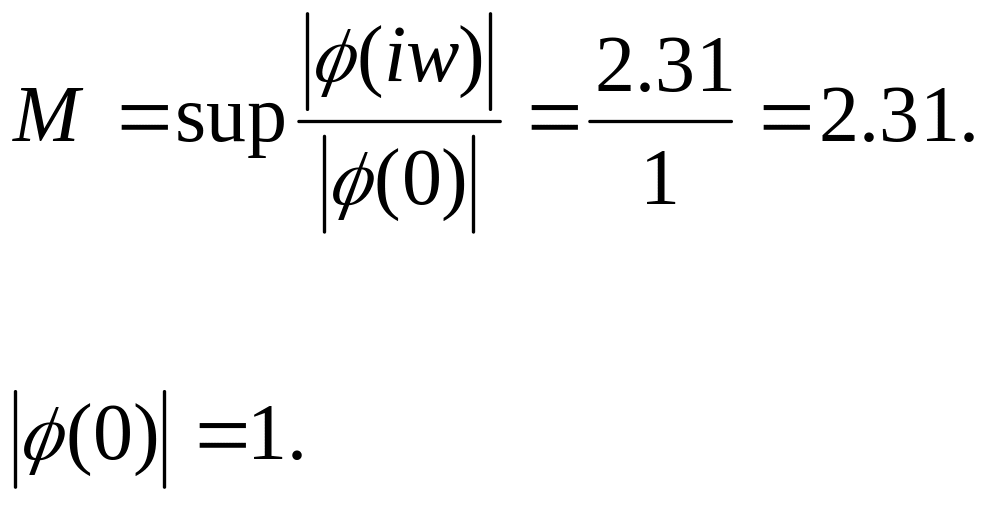
Резонансная частота:
.
Полоса пропускания:
.
.
Частота среза:
.
.
Время регулирования:
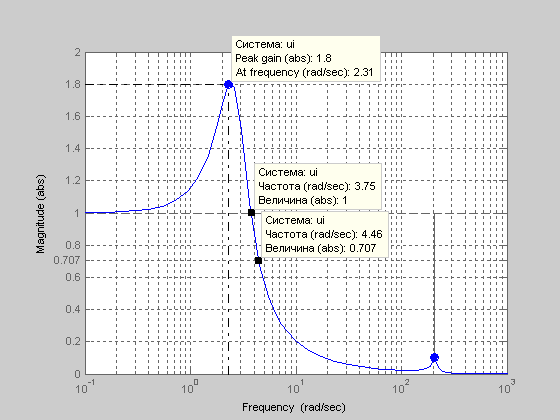
Рис.9
Найти уравнения состояния и выхода замкнутой системы. Проверить свойства управляемости и наблюдаемости этих вариантов:
А) Передаточная функция замкнутой системы:
Уравнение состояния и выхода имеют вид:
Составим систему для нахождения
коэффициентов
Используя Матлаб:
>>A=[2906976.7 1058139.5 494418.6 43093 28.99 1;
1058139.5 494418.6 43093 28.99 1 0;
494418.6 43093 28.99 1 0 0;
43093 28.99 1 0 0 0;
28.99 1 0 0 0 0;
1 0 0 0 0 0]
>>B=[2906976.7; 1046511.6; 75581.4;0;0;0]
>>C=inv(A)*B
Отсюда найденные коэффициенты:
Теперь составим уравнение состояния и выхода для нашей системы:
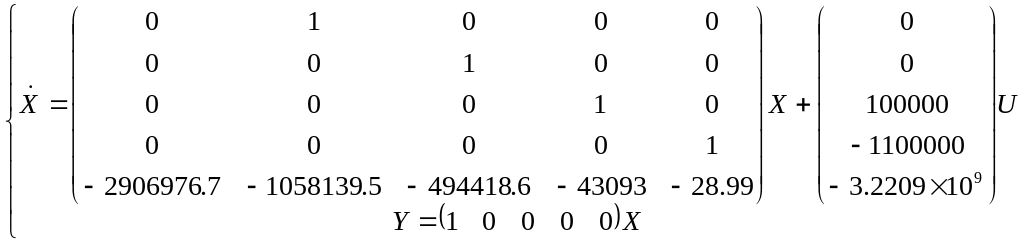
Б) Наблюдаемость и управляемость:
Для проверки свойств управляемости и наблюдаемости этих вариантов, воспользуемся пакетом Матлаб:
Код программы:
>>A1=[0 1 0 0 0;
0 0 1 0 0;
0 0 0 1 0;
0 0 0 0 1;
-2906976.7 -1058139.5 -494418.6 -43093 -28.99]
>>B1=[0;0;100000;-1100000;-3.2209e+009]
>>C1=[1 0 0 0 0]
>>K=[B1 A1*B1 A1^2*B1 A1^3*B1 A1^4*B1]
>>rank(K)
>>G=[C1;C1*A1;C1*A1^2;C1*A1^3;C1*A1^4]
>>rank(G)
K = 1.0e+018 *
0 0 0.0000 -0.0000 -0.0000
0 0.0000 -0.0000 -0.0000 0.0000
0.0000 -0.0000 -0.0000 0.0000 0.0001
-0.0000 -0.0000 0.0000 0.0001 -0.0063
-0.0000 0.0000 0.0001 -0.0063 -5.7451
ans =
4
G = 1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
ans =
5
Если ранг K=n , то система вполне управляемая;
Если ранг G=n , то система вполне наблюдаемая.
Но у нас выполняется только второе условие, следовательно, наша система неуправляемая, но наблюдаемая.
Список используемой литературы.