Оценить показатели качества замкнутой системы, определив нули и полюса передаточной функции:
Определим передаточную функцию замкнутой системы:
Найдем полюса и нули передаточной функции с использованием команд pole, zero:
>>s=tf('s');
>>w=(250*(0.1*s+1))/(s*(0.75*s+1)*(0.000441*s^2+0.0105*s+1))
>>h=(0.14*s^2)/(0.26*s+1)
>>u=w/(1+w*h)
>>ui=1/((1/w)+h+1)
>>pole(ui)
>>zero(ui)
Полюса(знаменатель)
ans =
1.0e+002 *
-0.0836 + 2.0690i
-0.0836 - 2.0690i
-0.0970
-0.0091 + 0.0248i
-0.0091 - 0.0248i
Нули (числитель)
ans =
-10.0000
-3.8462
Показатели качества:
Степень устойчивости:
Время регулирования:
Степень колебательности:
Колебательность связана с корневым показателем запаса устойчивости с так называемым затуханием. Комплексно сопряженные корни дают в выражении для переходного процесса вида
Найдем затухание амплитуды синусоидального
колебания за один период. При некотором
времени
эта амплитуда равна
Через один период
Затуханием за период называют величину
Подставляя значение амплитуды
,
получаем
Построить графики переходной функции и импульсной переходной функции определить показатели качества переходного процесса(для оценки времени регулирования принять ∆=3%):
Передаточная функция замкнутой системы:
Построим графики переходных функций во временных осях, используя пакет Matlab и команды step(sys) и impulse(sys).
Код программы:
>>t=0:0.02:7
>>s=tf('s');
>>w=(250*(0.1*s+1))/(s*(0.75*s+1)*(0.000441*s^2+0.0105*s+1))
>>h=(0.14*s^2)/(0.26*s+1)
>>u=w/(1+w*h)
>>ui=1/((1/w)+h+1)
>>step(ui,t)
>>impulse(ui,t)
Показатели качества переходного процесса:
Апериодическая функция - т.к. 1 максимум.
-
время, когда впервые достигается
-время
достижения максимума.
-время
регулирования.
3%
Перерегулирование:
Частота колебаний:
n – число колебаний за время регулирования =2.
Импульсная переходная функция
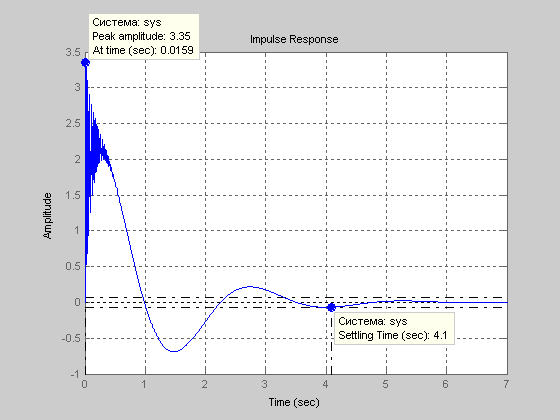
Рис.4
Переходная функция
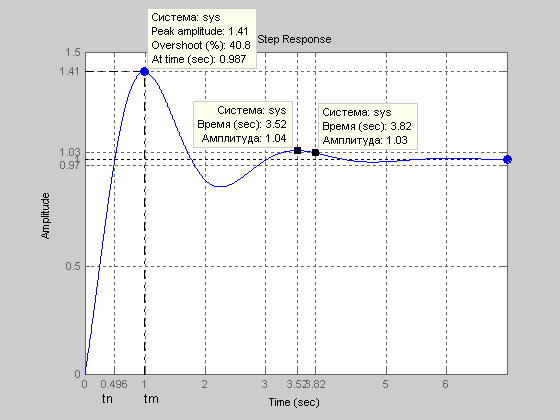
Рис.5
Найти аналитическое выражение импульсной переходной функции. Выделить составляющую найденной функции, соответствующую доминирующим полюсам, сравнить графики функции и указанной её составляющей:
Передаточная функция замкнутой системы:
С помощью программы Матлаб найдем полюса и вычеты для импульсной
функции системы. При использовании команды:
>>[R,P,K]=residue(num,den),
где результатом выполнения этой команды будут векторы-столбцы вычетов R и полюсов Р.
Так как у нас комплексно-сопряженные полюса и вычеты, то такую пару слагаемых объединим:
Общая формула:
R =
-0.8810 + 0.0471i
-0.8810 - 0.0471i
-0.0371
0.8995 - 1.0847i
0.8995 + 1.0847i
P =
1.0e+002 *
-0.0873 + 2.0686i
-0.0873 - 2.0686i
-0.0970
-0.0091 + 0.0248i
-0.0091 - 0.0248i
1)
Где оригинал:
2)
Оригинал:
3)
Где оригинал:
.
Импульсная переходная функция:
Выделим составляющую найденной функции, соответствующую доминирующим полюсам:
И определим ее график:
Код программы:
>>T=0:0.001:7
>>y1=1.8*exp(-0.91*T).*cos(-2.48*T)-2.17*exp(-0.91*T).*sin(-2.48*T)
>>ys=1.76*exp(-8.73*T).*cos(-206.86*T)-0.094*exp(-8.73*T).*sin(-206.86*T)-0.037*
*exp(-9.7*T)+1.8*exp(-0.91*T).*cos(-2.48*T)-2.17*exp(-0.91*T).*sin(-2.48*T)
>>plot(T,ys,T,y1),grid
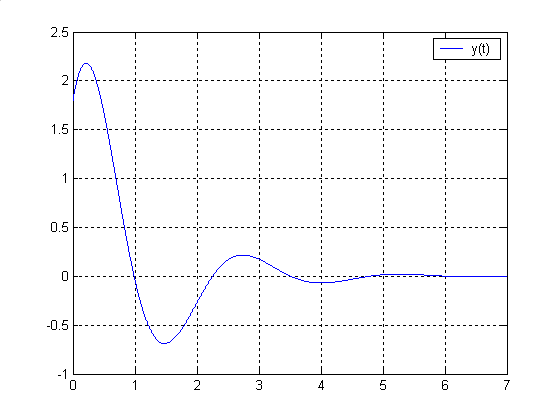
Рис.6
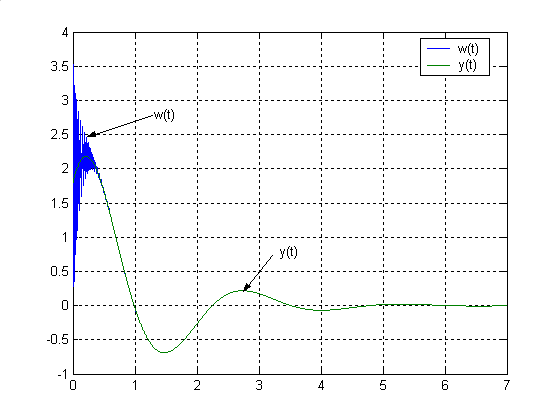
Рис.7