Балтийский Государственный Технический Университет им. Д.Ф. Устинова военмех
Кафедра мехатроники и робототехники
Курсовая работа по курсу Теория автоматического управления
Вариант 18
Студент: Шорохов А.С.
Группа: Н172.
Преподаватель: Коробова И.Л.
Санкт-Петербург
2009г.
Содержание
1. Определить передаточную функцию разомкнутой системы с коррекцией в цепи обратной связи и построить её логарифмические частотные характеристики.
Дать заключение об устойчивости замкнутой системы, определить запасы устойчивости.
2. Оценить показатели качества замкнутой системы, определив нули и полюса передаточной функции.
3. Построить графики переходной функции и импульсной переходной функции определить показатели качества переходного процесса (для оценки времени регулирования принять ∆=3%).
4. Найти аналитическое выражение импульсной переходной функции. Выделить составляющую найденной функции, соответствующую доминирующим полюсам, сравнить графики функции и указанной её составляющей.
5. Построить логарифмическую амплитудно-частотную характеристику замкнутой системы, определить полосу пропускания системы, резонансную частоту, показатель колебательности.
6. Найти уравнения состояния и выхода замкнутой системы. Проверить свойства управляемости и наблюдаемости этих вариантов.
Определить передаточную функцию разомкнутой системы с коррекцией в цепи обратной связи и построить её логарифмические частотные характеристики:
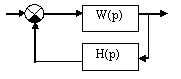
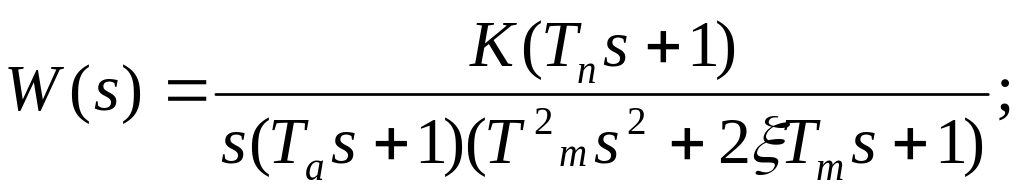
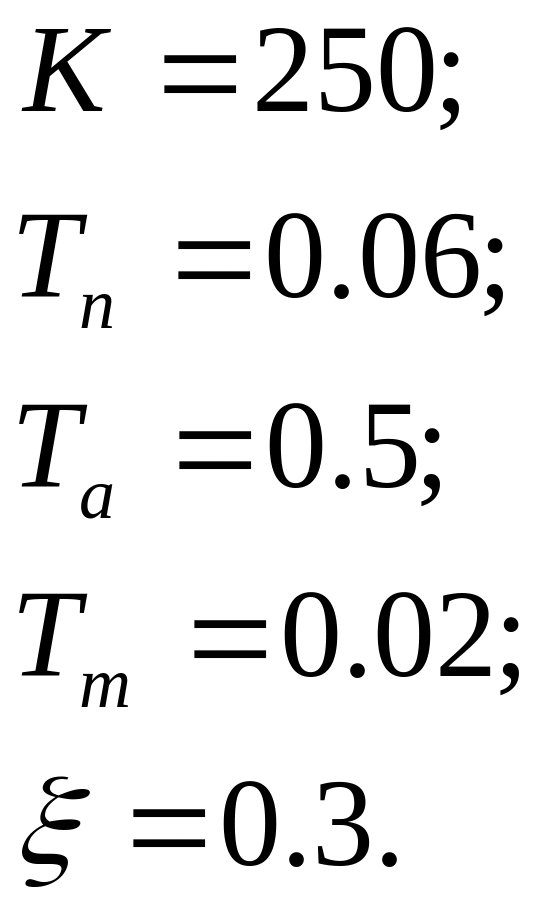
Передаточная функция разомкнутой системы:
Приведем к каноническому виду, используя команду zpk в пакете Матлаб:
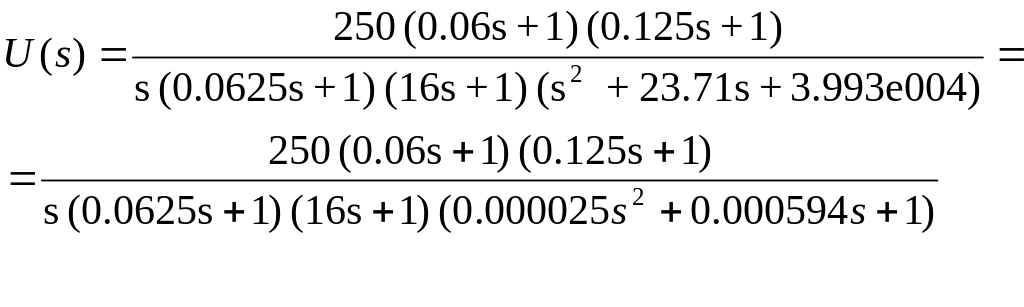
Находим ЛАЧХ и ФЧХ системы, используя пакет MATLAB:
>> num=[ 1.875,46.25,250];
>> den=[2.5e-005,0.001,1.008,16.26,1,0];
>> w=logspace(-3,3);
>> [gam,fi]=bode(num,den,w);
>> semilogx(w,20*log10(gam));
>> grid
>> title('L(w)')
>> semilogx(w,fi)
>> grid
>> title('fi')
>> title('fhase')
Рис.1
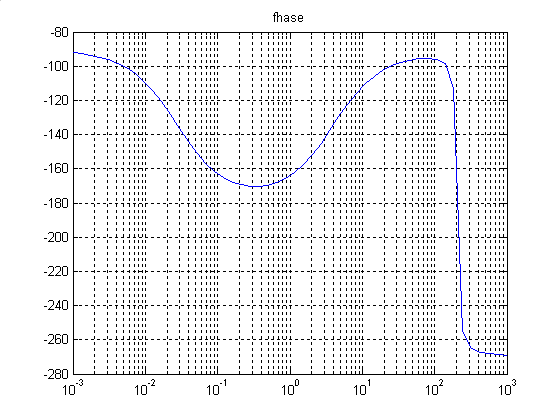
Рис.2
Дать заключение об устойчивости замкнутой системы, определить запасы устойчивости:
Разомкнутая система не имеет корней с положительной вещественной частью, поэтому
по критерию Найквиста, для асимптотической
устойчивости замкнутой системы необходимо
и достаточно, чтобы ЛФЧХ разомкнутой
системы в области частот, где ЛАЧХ
положительна, принимала значение -180˚
четное число раз или не принимала этого
значения, следовательно, данная система
устойчива, т.к. ЛФЧХ не принимала значение
ни разу в области частот, где ЛАЧХ
положительна.
Используя функцию
>>u=w/(1+wh)
>>[g f wg wf]=margin(u)
в пакете Matlab определим:
-запас устойчивости по фазе f и соответствующая частота wf:
f= 37.6265, wf = 2.9608
-запас устойчивости по амплитуде g и соответствующая частота wg:
g = 10.8944
20*lg(g) =20*lg(10.8944)=20,7441, wg = 206.9531
Запас устойчивости по фазе определяется на частоте, при которой ЛАЧХ принимает значение 0.
Запас устойчивости по амплитуде определяется на частоте, при которой ФЧХ принимает значение -180˚.
Построим ЛАЧХ и ЛФЧХ разомкнутой системы, используя Матлаб(bode(u)):
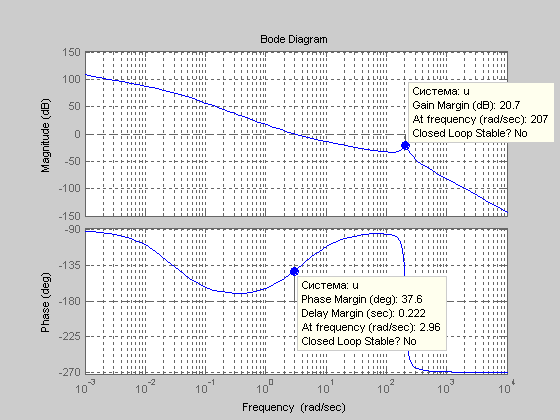
Рис.3