13. Свойства эквивалентных бесконечно малых.

1) Предел отношения двух б.м.ф. не изменится, если каждую из них заменить эквивалентной бесконечно малой.

Пусть и при , тогда

2) Разность б.м.ф. есть б.м.ф. более высокого порядка, чем каждая из них.

Пусть при , тогда , аналогично

3) Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.

Пусть и есть б.м.ф. при , причём - б.м.ф. высшего порядка, чем , т.е. .

Тогда , следовательно, при .

14. Первый замечательный предел.

- первый замечательный предел

Возьмем круг радиуса 1, обозначим радиальную меру угла MOB через х. Пусть . На рисунке , дуга MB численно равна центральному углу х, . Очевидно имеем .На основании соответствующих формул геометрии получаем , разделим неравенство на , получим или . Так как и , то по признаку о пределе промежуточной функции

15. Второй замечательный предел.

- второй замечательный предел

Мы знаем, что числовая последовательность имеет предел, равный е.

1. Пусть . Каждое значение х заключено между двумя целыми числами: ,где n = {x} – целая часть х. Отсюда следует , . Поэтому

Если , то , поэтому

,

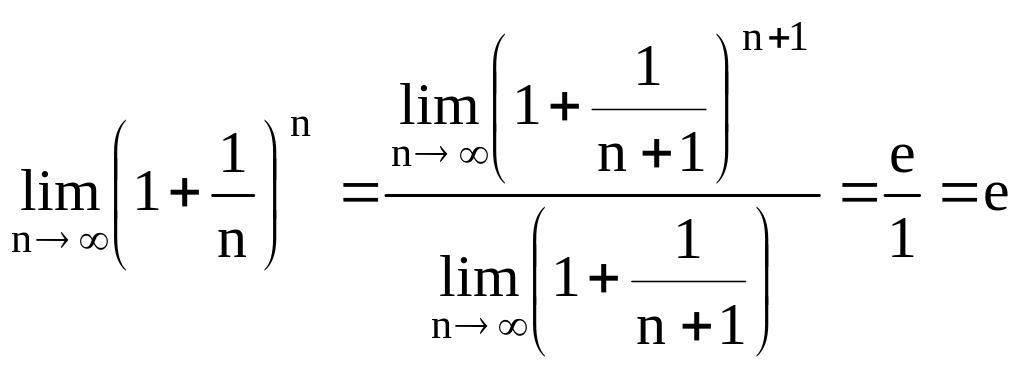По признаку о пределе промежуточной функции:

2. Пусть . Сделаем подстановку , тогда , следовательно

16. Непрерывность функции в точке.

Пусть функция определена в точке и некоторой окрестности этой точки. Функция называется непрерывной в точке , если существует предел функции в этой точке и он равен значению функции в этой точке

Функция непрерывна, если выполняются 3 условия:

1. функция определена в точке 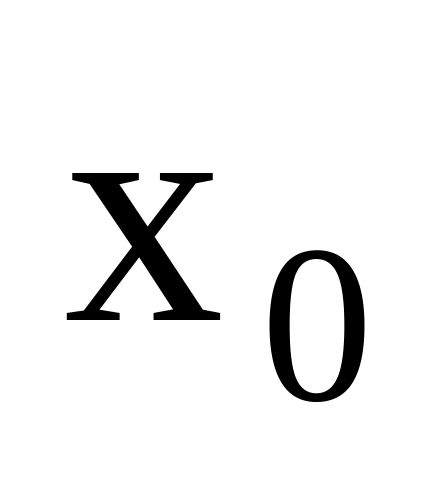и в ее окрестности

2. функция имеет предел при

3. предел функции в точке равен значению функции в этой точке

Это значит, что при нахождении предела некоторой функции f(x) можно перейти к пределу под знаком функции, т.е. в функцию f(x) вместо аргумента х подставить его предельное значение .

Пример. .

17. Свойства непрерывных функций.

1) Сумма, произведение и частное двух непрерывных функций есть функция непрерывная. (для частного кроме тех случаев, когда значение знаменателя равно нулю)

Пусть функции и непрерывны на некотором множестве Х и - любое значение из этого множества.

2) Пусть функции непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция , состоящая из непрерывных функций, непрерывна в точке .

В силу непрерывности функции , , т.е. при имеем . В следствии непрерывности функции имеем :

3) Если функция непрерывна и строго монотонна на [a;b] оси Ох, то обратная функция также непрерывна и монотонна на соответствующем отрезке [c;d] оси Oy.

18. Точки разрыва и их классификация.

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если - точка разрыва функции , то в ней не выполняется по крайней мере одно из условий непрерывности функции.

1. Функция определена в окрестности точки , но не определена в самой точке .

2. Функция определена в точке и в ее окрестности, но не существует предела f(x) при

Точка называется точкой разрыва первого рода функции , если в этой точке существуют конечные пределы слева и справа (односторонние пределы), т.е. и . При этом:

1. Если , то точка называется точкой устранимого разрыва.

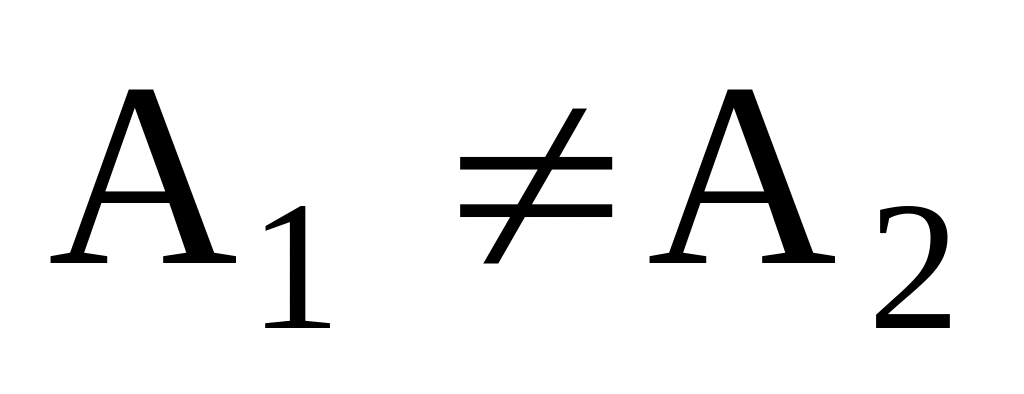2. Если , то точка называется точкой конечного разрыва

Величину называют скачком функции в точке разрыва первого рода.

Точка называется точкой разрыва второго рода функции , если по крайней мере один из односторонних пределов не существует или равен бесконечности.