23.Уравнения линейного трансформатора.

Пусть i₁, i₂ — мгновенные значения тока в первичной и вторичной обмотке соответственно, u₁ — мгновенное напряжение на первичной обмотке, R_H — сопротивление нагрузки. Тогда

Здесь L₁, R₁— индуктивность и активное сопротивление первичной обмотки, L₂, R₂— то же самое для вторичной обмотки, L₁₂— взаимная индуктивность обмоток. Если магнитный поток первичной обмотки полностью пронизывает вторичную, то есть если отсутствует поле рассеяния, то . Индуктивности обмоток в первом приближении пропорциональны квадрату количества витков в них.

Мы получили систему линейных дифференциальных уравнений для токов в обмотках. Можно преобразовать эти дифференциальные уравнения в обычные алгебраические, если воспользоваться методом комплексных амплитуд.

Для этого рассмотрим отклик системы на синусоидальный сигнал u₁=U₁ e^{-jω t} (ω=2π f, где f — частота сигнала, j — мнимая единица). Тогда i₁=I₁ e^{-jω t} и т. д., сокращая экспоненциальные множители получим

U₁=-jωL₁ I₁ -jωL₁₂ I₂+I₁ R₁

-jωL₂ I₂ -jω L₁₂ I₁+I₂ R₂ =-I₂ Z_н

Метод комплексных амплитуд позволяет исследовать не только чисто активную, но и произвольную нагрузку, при этом достаточно заменить сопротивление нагрузки R_н её импедансом Z_н. Из полученных линейных уравнений можно легко выразить ток через нагрузку, воспользовавшись законом Ома— напряжение на нагрузке, и т. п.

.Уравнения идеального трансформатора

Идеальный трансформатор — трансформатор, у которого отсутствуют потери энергии на нагрев обмоток и потоки рассеяния обмоток^[8]. В идеальном трансформаторе все силовые линии проходят через все витки обеих обмоток, и поскольку изменяющееся магнитное поле порождает одну и ту же ЭДС в каждом витке, суммарная ЭДС, индуцируемая в обмотке, пропорциональна полному числу её витков^[9]. Такой трансформатор всю поступающую энергию из первичной цепи трансформирует в магнитное поле и, затем, в энергию вторичной цепи. В этом случае поступающая энергия равна преобразованной энергии:

Где

P₁ — мгновенное значение поступающей на трансформатор мощности, поступающей из первичной цепи,

P₂ — мгновенное значение преобразованной трансформатором мощности, поступающей во вторичную цепь.

Соединив это уравнение с отношением напряжений на концах обмоток, получим уравнение идеального трансформатора:

Таким образом получаем, что при увеличении напряжения на концах вторичной обмотки U₂, уменьшается ток вторичной цепи I₂.

Для преобразования сопротивления одной цепи к сопротивлению другой, нужно умножить величину на квадрат отношения.^[10] Например, сопротивление Z₂ подключено к концам вторичной обмотки, его приведённое значение к первичной цепи будет . Данное правило справедливо также и для вторичной цепи: .

24.Режимы работы трансформатора

1. Режим холостого хода. Данный режим характеризуется разомкнутой вторичной цепью трансформатора, вследствие чего ток в ней не течёт. С помощью опыта холостого хода можно определить КПД трансформатора, коэффициент трансформации, а также потери в стали.

2. Нагрузочный режим. Этот режим характеризуется замкнутой на нагрузке вторичной цепи трансформатора. Данный режим является основным рабочим для трансформатора.

3. Режим короткого замыкания. Этот режим получается в результате замыкания вторичной цепи накоротко. С его помощью можно определить потери полезной мощности на нагрев проводов в цепи трансформатора. Это учитывается в схеме замещения реального трансформатора при помощи активного сопротивления.

16.. Последовательное соединение конденсатора и катушки индуктивности. Понятие о резонансе напряжений

6.5.1. Общие сведения

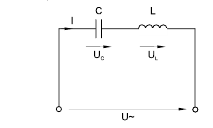
Когда по цепи (рис. 6.4.1) с последовательным соединением конденсатора и ка-

тушки индуктивности протекает один и тот же синусоидальный ток I, напряжение на

конденсаторе UC отстает от тока I на 900, а напряжение на катушке индуктивности UL

опережает ток на 900. Эти напряжения находятся в противофазе (повернуты относи-

тельно друг друга на 1800).

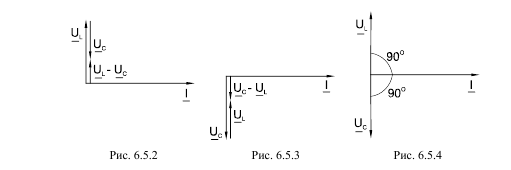
Если одно из напряжений больше другого, цепь оказывается либо преимущест-

венно индуктивной (рис. 6.5.2), либо преимущественно емкостной (рис. 6.5.3). Если

напряжения UL и UС имеют одинаковые значения и компенсируют друг друга, то сум-

марное напряжение на участке цепи L – C оказывается равным нулю. Остается только

небольшая составляющая напряжения на активном сопротивлении катушки и прово-

дов. Такое явление называется резонансом напряжений (рис. 6.5.4).

При резонансе напряжений реактивное сопротивление цепи

X = XL – XC

оказывается равным нулю. При заданных значениях L и C резонанс может быть получен путем изменения частоты.

Рис. 6.4.1 Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности

Поскольку XL = ωL, а XC = 1 / ωC, то резонансная частота ω0 может быть определена из уравнения:

ω0L – 1 / ω0C = 0,

откуда

ω0=1/LC и f0=ω0/2π=1/2π√LC

Полное сопротивление цепи при резонансе оказывается равным небольшому ак-

тивному сопротивлению катушки, поэтому ток в цепи совпадает по фазе с напряжени-

ем и может оказаться довольно большим даже при маленьком приложенном напряже-

нии. При этом напряжения UL и UC могут существенно (в десятки раз!) превышать

приложенное напряжение.