11.Моменты инерции

Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.

Момент инерции относительно точки

Скалярная величина

или

называется полярным моментом инерции относительно точки О. d – расстояние от текущей точки до точки О.

Момент инерции относительно оси

Скалярная величина или

называется моментом инерции относительно оси l. r – расстояние от точки до оси.

Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции.

Величина называется радиусом инерции.

Момент инерции относительно оси через радиус инерции относительно этой же оси определяется выражением .

Моменты инерции относительно осей координат

Центробежные моменты инерции

Установим зависимость между моментами инерции относительно параллельных осей, одна из которых проходит через центр масс.

Теорема о моментах инерции относительно параллельных осей. (Теорема Штейнера)

Момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.

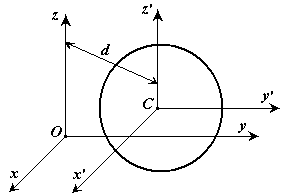
Доказательство: Пусть имеется две декартовы системы координат и , оси которых параллельны. Начало системы находится в центре масс системы. Докажем теорему для осей и .

Координаты связаны между собой соотношениями:

, ,

, , .

Следовательно , что и требовалось доказать.

Главными осями инерции называются оси, в которых центробежные моменты инерции равны нулю.

Моменты инерции тела относительно главных осей инерции называются главными моментами инерции тела.

Тензор инерции и тензор инерции для главных осей:

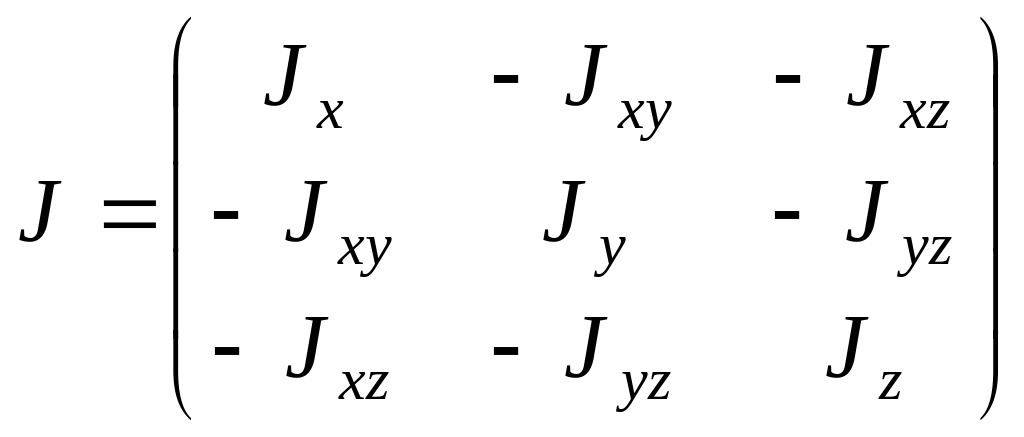
12.Ускорение точки

П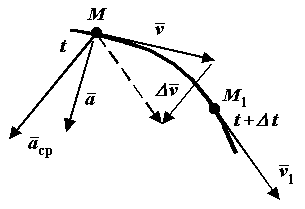 усть движущаяся точка М в момент времени имеет скорость . В другой момент времени эта точка будет занимать положение М₁ и иметь скорость . Чтобы изобразить прираще-ние скорости за время , перенесем вектор параллельно самому себе в точку М.

Рис. 2-3

Средним ускорением точки за время называется отношение вектора приращения скорости к изменению времени .

(2-3)

Ускорением точки в момент времени называется предел к которому стремится среднее ускорение при , стремящемся к нулю. Ускорение точки равно первой производной по времени от скорости точки или второй производной по времени от радиус-вектора.

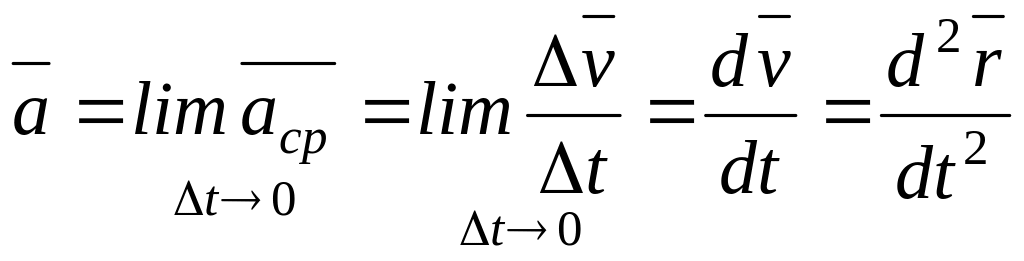(2-4)

Ускорение при координатном способе задания движения

 

1. Координатный способ задания движения

                 При координатном способе задания движения:

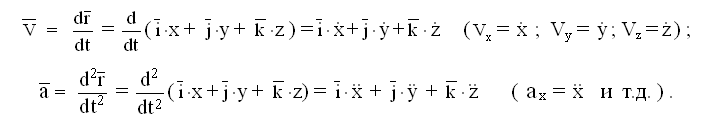
         То есть и вектор скорости точки,  и вектор ее ускорения при координатном способе задания движения определяются через их проекции на координатные оси.  А как найти модуль каждого вектора  и его направляющие  косинусы,  повторять,  наверное,  не стоит.

 

Проекция ускорения точки на какую-либо координатную ось равна второй производной по времени от соответствующей координаты этой точки.

Модуль ускорения и направляющие косинусы равны:

(2-8)

(2-9)

Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:

Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда