46.Поступательное движение твердого тела.

Поступательное движение — это механическое движение системы точек (тела), при котором любой отрезок прямой, связанный с движущимся телом, форма и размеры которого во время движения не меняются, остается параллельным своему положению в любой предыдущий момент времени.

47.Дифференциальные уравнения движения материальной точки.

Из второго закона Ньютона динамики материальной точки

(1.1)

получаются две наиболее распространенные формы дифференциальных уравнений движения:

– дифференциальные уравнения движения точки в координатной форме

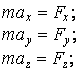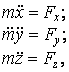или (1.2)

Где – проекции ускорения на оси декартовых координат, – проекции силы на те же оси декартовых координат;

– дифференциальные уравнения движения точки в естественной форме

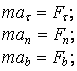или (1.3)

Где – проекции ускорения на естественные оси координат;

S– дуговая координата точки; – скорость точки; – радиус кривизны траектории; – проекции силы на естественные оси координат.

С помощью дифференциальных уравнений (1.2) и (1.3) можно решить любую задачу динамики свободной материальной точки.

48.Теорема об изменении количества изменения точки

d(mV) = Fdt (1)

Произведение mV назовем количеством движения точки, произведение Fdt - элементарным импульсом силы (равнодействующей), что позволяет сформулировать теорему об изменении количества движения материальной точки в дифференциальной форме: дифференциал от количества движения материальной точки равен элементарному импульсу сил, приложенных к точке.

49. Векторные скорости и ускорения точек тела

Скорость точки по модулю и направлению можно представить векторным произведением

(5-3)

где - радиус-вектор точки М, проведенный из произвольной точки оси вращения .

Э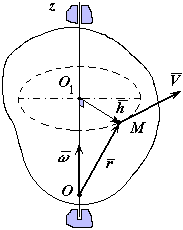 то выражение называется векторной формулой Эйлера.

Доказательство. Вектор перпендикулярен плоскости, в которой расположены векторы и , следовательно, по направлению он совпадает со скоростью . Модуль векторного произведения Таким образом, векторное произведение по модулю и направлению определяет скорость точки.