
- •4.Пара сил
- •Условия равновесия пар сил.
- •5.Законы Кулона
- •6.Скорости и ускорения точек тела при вращении.
- •11.Моменты инерции
- •12.Ускорение точки
- •1. Координатный способ задания движения
- •2.Ускорение точки при естественном способе задания движения.
- •15.Теорема об изменении кинетической энергии материальной точки.
- •Элементарный и полный импульс силы.
- •19. Сложение пар сил. Условие равновесия сил.
- •20.Динамические дифференциальные уравнения относительно движения материальной точки. Динамическая теорема Кориолиса
- •21.Разложение плоского движения твердого тела на поступательное и вращательное движение. Угловая скорость и угловое ускорение тела при плоском движении
- •22.Зависимость между моментами силы относительно оси и относительно любой очки лежащей на оси
- •23. Теорема о моменте равнодействующей силы (вариньона)
- •24. Построение и вычисление ускорения кариолиса
- •25. Аксиомы классической механики
- •26, Условия равновесия системы
- •Скорость точки
- •Нахождение скорости при естественном способе задания движения.
- •28. Скорость точки при векторном способе задания движения.
- •Определение скорости при координатном способе задания движения.
- •Нахождение скорости при естественном способе задания движения.
- •29. Две основные задачи динамики точки:
- •30. Кинетическая энергия системы.
- •31 Кинетическая энергия твердого тела.
- •33 . Дифференциальные уравнения сферического и свободного движений твердого тела
- •35) Условия равновесия в геометрической и аналитической формах.
- •Условия равновесия для частных случаев произвольной системы с ил в аналитической форме.
- •39) Теорема о скоростях точек плоской фигуры.
- •44)Приведение системы сходящихся сил к равнодействующей
- •Условия равновесия системы сходящихся сил
- •46.Поступательное движение твердого тела.
- •47.Дифференциальные уравнения движения материальной точки.
- •48.Теорема об изменении количества изменения точки
44)Приведение системы сходящихся сил к равнодействующей
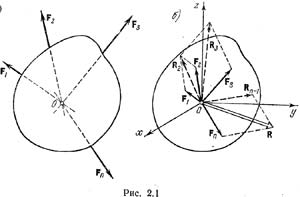
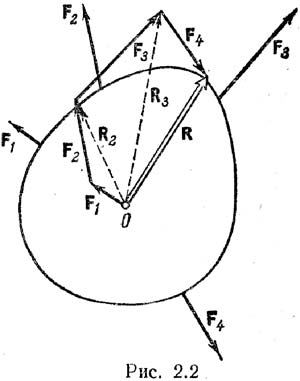
Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке. Докажем теорему: Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна сумме всех этих сил и проходит через точку пересечения их линий действия. Пусть задана система сходящихся сил F1, F2, F3, ..., Fn, приложенных к абсолютно твердому телу (рис. 2.1, а). Перенесем точки приложения сил по линиям их действия в точку пересечения этих линий (21, б). Получили сист сил, прил к одной точке. Она эквивалентна заданной. Сложим F1 и F2, получим их равнодействующую: R2=F1+F2. Сложим R2 с F3: R3=R2+F3=F1+F2+F3. Сложим F1+F2+F3+…+Fn=Rn=R=åFi. Ч.т.д. Вместо параллелограммов можно построить силовой многоугольник. Пусть система состоит из 4 сил (рис 2.2.). От конца вектора F1 отложим вектор F2. Вектор, соединяющий начало О и конец вектора F2, будет вектором R2. Далее отложим вектор F3 помещая его начало в конце вектора F2. Тогда мы получим вектор R8, идущий от точки О к концу вектора F3. Точно так же добавим вектор F4; при этом получим, что вектор, идущий от начала первого вектора F1 к концу вектора F4, является равнодействующей R. Такой пространственный многоугольник называется силовым. Если конец последней силы не совпадает с началом первой силы, то силовой многоугольник назразомкнутый. Если для нах равнодействующей исп прав геометр, то этот способ наз геометрическим.
Больше пользуются аналитическим способом для определения равнодействующей. Проекция суммы векторов на некоторую ось равна сумме проекций на ту же ось слагаемых векторов, получим Rx=åFkx=F1x+F2x+…+Fnx; Ry=åFky=F1y+F2y+…+Fny; Rz=åFkz=F1z+F2z+…+Fnz; где Fkx, Fky, Fkz– проекции силы Fk на оси, а Rx, Ry, Rz– проекции равнодействующей на те же оси. Проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на соответствующие оси. Модуль равнодействующей R равен: R=(Rx2+Ry2+Rz2)1/2. Направляющие косинусы равны: cos(x,R)=Rx/R, cos(y,R)=Ry/R, cos(z,R)=Rz/R. Если силы распол в пл-ти то всё аналогично, отсутствует ось Z.
Условия равновесия системы сходящихся сил
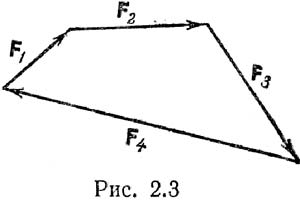
(F1, F2, ...,Fn)~R => для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы их равнодействующая равнялась нулю: R = 0. Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замкнут (рис. 2.3). Это условие используется при графическом решении задач для плоских систем сил. Векторное равенство R=0 эквивалентно трем скалярным равенствам: Rx=åFkx=F1x+F2x+…+Fnx=0; Ry=åFky=F1y+F2y+…+Fny=0; Rz=åFkz=F1z+F2z+…+Fnz=0; где Fkx, Fky, Fkz– проекции силы Fk на оси, а Rx, Ry, Rz– проекции равнодействующей на те же оси. Т. е. для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, находится ли в равновесии заданная система сил.
45) Поступательным называется такое движение твердого тела, при котором любая прямая линия, проведенная в теле, перемещается, оставаясь параллельной своему начальному положению. При поступательном движении:
все точки тела описывают одинаковые траектории;
скорости всех точек тела одинаковые в данный момент времени ;
ускорение всех точек тела одинаковые в данный момент времени ;
Поступательное движение твердого тела полностью определяется движением любой одной его точки, т.е. кинематика поступательного движения может быть сведена к кинематике точки.
Теорема.При поступательном движении твердого тела все его точки движутся по одинаковым и параллельным траекториям и имеют в каждый данный момент времени равные по модулю и направлению скорости и ускорения.
Доказательство.
Для доказательства теоремы рассмотрим
движение отрезка прямой
![]() ,
проведенного в теле, с
,
проведенного в теле, с овершающем
поступательное движение (рис. 2.10). Из
определения поступательного движения
следует, что в каждый данный момент
времени отрезок
,
занимающий последовательно положения
овершающем
поступательное движение (рис. 2.10). Из
определения поступательного движения
следует, что в каждый данный момент
времени отрезок
,
занимающий последовательно положения![]() ,
,
![]() ,
,
![]() и т.д., остается параллельным своему
первоначальному положению. Учитывая
это и то что
и т.д., остается параллельным своему
первоначальному положению. Учитывая
это и то что
![]() ,
делаем вывод, что ломаные линии
,
делаем вывод, что ломаные линии
![]() и
и
![]() параллельны и при наложении совпадут
всеми своими точками. При бесконечном
уменьшении промежутков времени между
рассматриваемыми положениями отрезка
мы видим, что точка
параллельны и при наложении совпадут
всеми своими точками. При бесконечном
уменьшении промежутков времени между
рассматриваемыми положениями отрезка
мы видим, что точка
![]() и точка
и точка
![]() описывают одинаковые кривые, т. е.
кривые, совпадающие при наложении.
описывают одинаковые кривые, т. е.
кривые, совпадающие при наложении.
Для
доказательства второй части теоремы
заметим, что
![]() .
(2.27)
.
(2.27)
Возьмем
производные по времени от левой и правой
частей![]() .Так
как
.Так
как
![]() ,
то
,
то
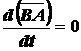 .
.
Тогда![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
