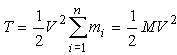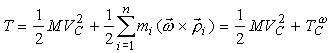- •4.Пара сил
- •Условия равновесия пар сил.
- •5.Законы Кулона
- •6.Скорости и ускорения точек тела при вращении.
- •11.Моменты инерции
- •12.Ускорение точки
- •1. Координатный способ задания движения
- •2.Ускорение точки при естественном способе задания движения.
- •15.Теорема об изменении кинетической энергии материальной точки.
- •Элементарный и полный импульс силы.
- •19. Сложение пар сил. Условие равновесия сил.
- •20.Динамические дифференциальные уравнения относительно движения материальной точки. Динамическая теорема Кориолиса
- •21.Разложение плоского движения твердого тела на поступательное и вращательное движение. Угловая скорость и угловое ускорение тела при плоском движении
- •22.Зависимость между моментами силы относительно оси и относительно любой очки лежащей на оси
- •23. Теорема о моменте равнодействующей силы (вариньона)
- •24. Построение и вычисление ускорения кариолиса
- •25. Аксиомы классической механики
- •26, Условия равновесия системы
- •Скорость точки
- •Нахождение скорости при естественном способе задания движения.
- •28. Скорость точки при векторном способе задания движения.
- •Определение скорости при координатном способе задания движения.
- •Нахождение скорости при естественном способе задания движения.
- •29. Две основные задачи динамики точки:
- •30. Кинетическая энергия системы.
- •31 Кинетическая энергия твердого тела.
- •33 . Дифференциальные уравнения сферического и свободного движений твердого тела
- •35) Условия равновесия в геометрической и аналитической формах.
- •Условия равновесия для частных случаев произвольной системы с ил в аналитической форме.
- •39) Теорема о скоростях точек плоской фигуры.
- •44)Приведение системы сходящихся сил к равнодействующей
- •Условия равновесия системы сходящихся сил
- •46.Поступательное движение твердого тела.
- •47.Дифференциальные уравнения движения материальной точки.
- •48.Теорема об изменении количества изменения точки
31 Кинетическая энергия твердого тела.
Очень часто материальная система представляет твердое тело или систему твердых тел. Поэтому нужно уметь вычислять кинетическую энергию твердого тела при различных видах его движения.
1. В случае поступательного движения скорости всех его точек одинаковы и равны V. Тогда по формуле (24)
|
(26) |
2. При вращении тела вокруг неподвижной оси Vi = ωhzi, где ω - угловая скорость вращения тела вокруг неподвижной оси z, а hzi - расстояние от точки до этой оси. По формуле (24) получаем
|
(27) |
г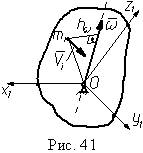 де Jz -
момент инерции тела относительно оси
вращения z.
де Jz -
момент инерции тела относительно оси
вращения z.
3. При движении тела с одной неподвижной точкой (сферическое движение) скорость любой его точки с массой mi выражается как Vi = ωhω, где hω - расстояние от точки до мгновенной оси вращения, на которой лежит вектор угловой скорости ω (рис. 41). То есть распределение скоростей точек тела в каждое мгновение времени такое же, как при вращении вокруг неподвижной оси. Поэтому согласно формуле (27) получим выражение для кинетической энергии твердого тела при его сферическом движении:
|
(28) |
где Jω - момент инерции относительно оси вращения.
Кинетическую энергию вычисляем в связанной с телом системе координат Ox1y1z1 (рис. 43), так как в ней элементы тензора инерции постоянны. Положение оси вращения в твердом теле определим направляющими косинусами
![]()
Тогда
![]()
Подставляя это выражение в формулу (28), имеем
|
(29) |
Если оси Ox1y1z1 будут главными осями инерции, то формула (29) упрощается:
|
(30) |
а если они будут главными центральными осями инерции, то кинетическая энергия тела будет минимальной.
Из формулы (29) можно получить и формулу кинетической энергии тела, вращающегося вокруг неподвижной оси. Для этого нужно положить в (29) ωx1 = ωy1 = 0, тогда ось Oz1 станет неподвижной и будет совпадать с неподвижной осью вращения, то есть ωz1 = ω.
4.
В общем случае свободного движения
твердого тела дополнительно к системам
координат, используемым при выводе
теоремы Кенига, введем систему
координат Cx1y1z1,
неизменно связанную с телом (рис. 42). Так
как переносное движение тела поступательное,
относительная скорость точки тела Vir =
ω ![]() ρi,
где ω -
угловая скорость вращения тела и
связанной с ним системы координат в
кениговой, а ρi -
радиус-вектор, определяющий положение
точки в кениговой и связанной системах
координат, начала которых находятся в
центре масс тела. Тогда, так как твердое
тело является неизменяемой системой
материальных точек, по формуле (25)
ρi,
где ω -
угловая скорость вращения тела и
связанной с ним системы координат в
кениговой, а ρi -
радиус-вектор, определяющий положение
точки в кениговой и связанной системах
координат, начала которых находятся в
центре масс тела. Тогда, так как твердое
тело является неизменяемой системой
материальных точек, по формуле (25)
|
(31) |
где TCω - кинетическая энергия тела возникающая только из-за вращения тела вокруг центра масс. Следовательно, теорему Кенига для свободного твердого тела можно сформулировать так:кинетическая энергия свободного твердого тела равна сумме кинетической энергии его поступательного (переносного) движения вместе с центром масс и кинетической энергии вращения тела вокруг (относительно) центра масс.
Останавливая переносное движение, видим что относительным движением, естественно, является сферическое движение вокруг неподвижного центра масс - точки C, поэтому по формуле (28)
![]()
Следовательно, для вычисления TCω свободного твердого тела нужно применять формулы (29) и (30), учитывая что связанные с телом оси обязательно должны быть центральными.
При плоском движении твердого тела, как показано в кинематике, вектор угловой скорости ω всегда перпендикулярен к плоскости движения xOy, совпадая с поступательно перемещающимися осями Cz* и Cz1. Останавливая переносное поступательное движение, видим что относительным движением является вращение вокруг неподвижной оси Cz1, поэтому по формуле (27)
![]()
где JCz1 - момент инерции относительно оси, связанной с телом , проходящей через центр масс перпендикулярно плоскости движения. По теореме Кенига (31) имеем
|
(32) |
При плоском движении ось Cz1 не меняет своего положения в теле и направления в инерциальном пространстве, что существенно упрощает вычисление кинетической энергии тела в плоском движении по сравнению с вычислением кинетической энергии свободного твердого тела.
32Теорема. Ускорение
точки плоской фигуры
равно сумме ускорения полюса ![]() и
ускорения данной точки во вращательном
движении вокруг полюса
и
ускорения данной точки во вращательном
движении вокруг полюса ![]()
![]() или
или ![]() .
.
При
плоском движении с учетом характера
движения осестремительное ускорение
называется центростремительным и
обозначается символом ![]() .
.
Следствие. Проекции ускорений двух точек плоской фигуры на направление вектора, соединяющего эти точки, связаны равенством
![]() .
.
Другим следствием теоремы об ускорениях точек при плоском движении твердого тела является равенство:
![]() .
.
Вводя
в рассмотрение вектор углового
ускорения ![]() при
плоском движении, теорема может быть
записана в виде:
при
плоском движении, теорема может быть
записана в виде:
![]() или
или ![]() .
.
Проецируя на координатные оси, находим
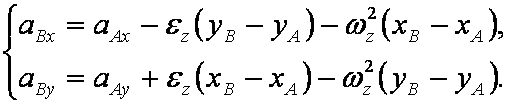 (2.4.2)
(2.4.2)
Эти уравнения могут быть использованы для определения неизвестных величин. При этом возможны два случая:
а)
Если направление ускорения точки ![]() известно
(или известны направления его составляющих),
то из системы уравнений (2.4.2) находится
ускорение этой точки, а также
известно
(или известны направления его составляющих),
то из системы уравнений (2.4.2) находится
ускорение этой точки, а также ![]() .
При этом если знак
совпадает
с
.
При этом если знак
совпадает
с ![]() ,
то вращение плоской фигуры ускоренное.
,
то вращение плоской фигуры ускоренное.
б) Если расстояние от какой-либо точки (например, точки A) плоской фигуры до мгновенного центра скоростей постоянно, то используется другой алгоритм решения. Сначала определяются скорость и ускорение точки A и эта точка принимается за полюс. Далее находится угловое ускорение по формуле
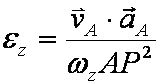 или
или 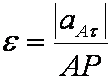 .
(2.4.3)
.
(2.4.3)
Затем
из равенств (2.4.2) получаем проекции
вектора ускорения произвольной
точки ![]() плоской
фигуры на оси координат.
плоской
фигуры на оси координат.
Кинетический момент точки и системы относительно центра и оси
Рассмотрим систему материальных точек с массами m1m2....mn, имеющих в данный момент скорости v1v2.....vn относительно инерциальной системы отсчета. Выберем произвольный центр О (Рис.1). Кинетическим моментом точки mjотносительно центра О называется вектор момента ее количества движения относительно этого центра.
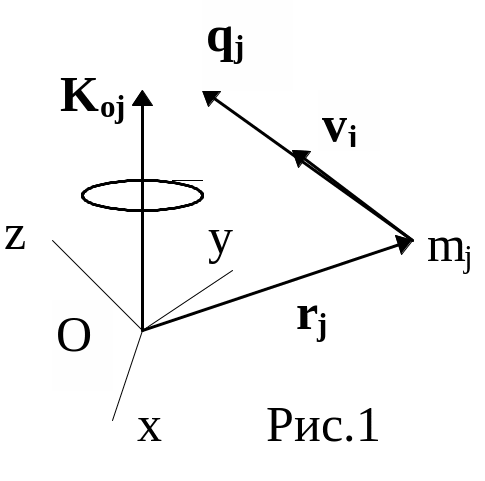
Известно, что векторное умножение можно записать через присоединенную матрицу первого сомножителя радиуса вектора r.
Опуская индекс j, запишем матричное выражение в осях xyz c началом в О:
Ko=mRv (2)
где R- кососимметричная присоединенная матрица столбца r
![]() =m
=m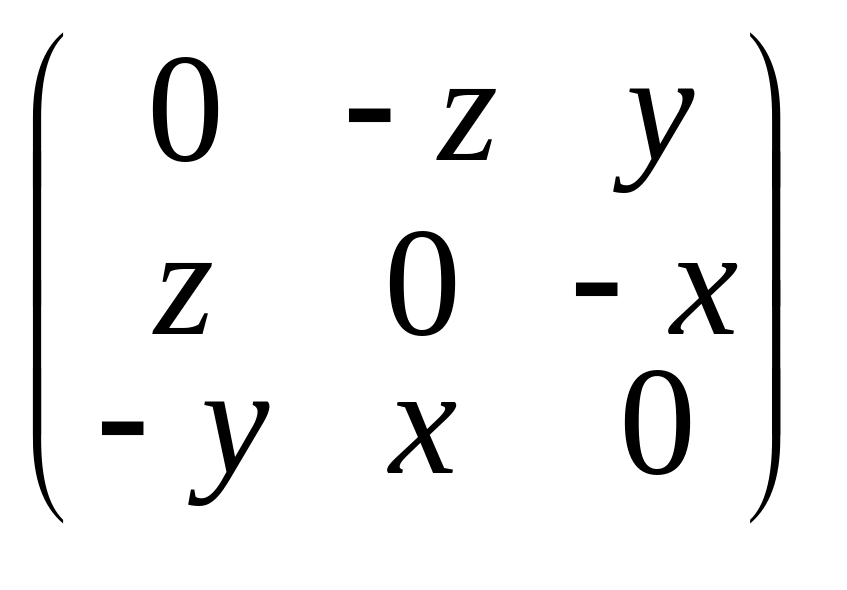
![]() =m
=m![]() (3)
(3)
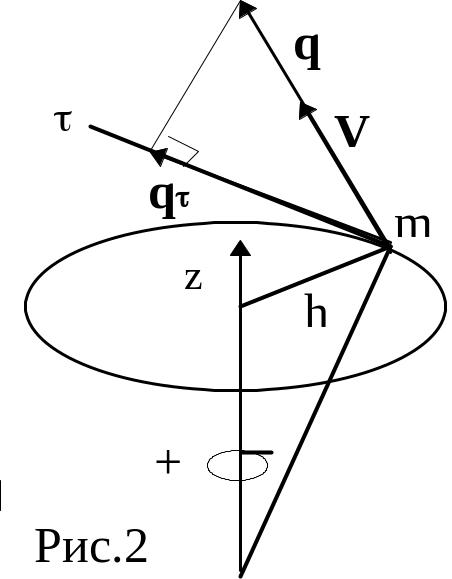
KZ= +qh (4)
Момент обращается в ноль, если вектор количества движения (скорость точки) лежит в одной плоскости с осью (параллелен или пересекает ось)
Теорема об изменении количества движения.
Рассмотрим систему, состоящую из п материальных точек. Составим для этой системы дифференциальные уравнения движения и сложим их почленно. Тогда получим:
![]() .
.
Последняя сумма по свойству внутренних сил равна нулю. Кроме того,
![]()
Окончательно находим:
![]() .
.
Уравнение выражает теорему об изменении количества движения системы в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил. В проекциях на координатные оси будем иметь:
![]()
![]()
![]()
Найдем
другое выражение теоремы. Пусть в
момент ![]() количество
движения системы равно
количество
движения системы равно ![]() , а
в момент
, а
в момент ![]() становится
равным
становится
равным ![]() .
Тогда, умножая обе части равенства
на dt и
интегрируя, получим:
.
Тогда, умножая обе части равенства
на dt и
интегрируя, получим:
![]()
или
![]()
так как интегралы, стоящие справа, дают импульсы внешних сил.
Уравнение выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
В проекциях на координатные оси будем иметь:
![]()
![]()
![]()
Укажем
на связь между доказанной теоремой и
теоремой о движении центра масс.
Так как ![]() то,
подставляя это значение в равенство и
учитывая, что
то,
подставляя это значение в равенство и
учитывая, что ![]() ,
мы получим
,
мы получим ![]() .
.
Следовательно, теорема о движении центра масс и теорема об изменении количества движения системы представляют собой, по существу, две разные формы одной и той же теоремы. В тех случаях, когда изучается движение твердого тела (или системы тел), можно в равной мере пользоваться любой из этих форм.
Практическая ценность теоремы состоит в том, что она позволяет исключить из рассмотрения наперед неизвестные внутренние силы (например, силы давления друг на друга частиц жидкости).
Закон сохранения количества движения.
Из теоремы об изменении количества движения системы можно получить следующие важные следствия:
1) Пусть сумма всех внешних сил, действующих на систему, равна нулю:
![]()
Тогда
из уравнения ![]() следует,
что при этом
следует,
что при этом ![]() .
Таким образом, если
сумма всех внешних сил, действующих на
систему, равна нулю, то вектор количества
движения системы будет постоянен по
модулю и направлению.
.
Таким образом, если
сумма всех внешних сил, действующих на
систему, равна нулю, то вектор количества
движения системы будет постоянен по
модулю и направлению.
2) Пусть внешние силы, действующие на систему, таковы, что сумма их проекций на какую-нибудь ось (например Оx) равна нулю:
![]()
Тогда
из уравнения ![]() следует,
что при этом
следует,
что при этом ![]() .
Таким образом, если
сумма проекций всех действующих внешних
сил на какую-нибудь ось равна нулю, то
проекция количества движения системы
на эту ось есть величина постоянная.
.
Таким образом, если
сумма проекций всех действующих внешних
сил на какую-нибудь ось равна нулю, то
проекция количества движения системы
на эту ось есть величина постоянная.