Нахождение скорости при естественном способе задания движения.

При движении точки по траектории радиус-вектор будет меняться с изменением дуговой координаты, а сама дуговая координата является функцией времени, то есть радиус-вектор является сложной функцией времени r = r (s(t)). По формуле (1) выразим вектор скорости точки:

(14)

Р ассмотрим вектор dr / ds. Согласно формуле (14), этот вектор направлен по касательной к траектории, так как скорость направлена по касательной, а так как при Δs 0 предел отношения длины дуги |Δs| к длине ее хорды MM₁ = Δr (рис. 61) равен единице, то по модулю он равен единице. Следовательно,

(15)

где является единичным вектором касательной к траектории в точке M.

Вектор всегда направлен в сторону возрастания дуговой координаты. На рис. 61 показан случай, когда Δs > 0 (дуговая координата точки больше координаты точки M₁). Сам вектор Δ /Δs направлен в сторону вектора Δ , в сторону положительного отсчета дуги. Когда Δs < 0 , точка M₁ будет находиться ближе к началу отсчета, чем точка M, вектор Δ изменит направление, а вектор Δ /Δs будет направлен в сторону, противоположную Δ (Δs - отрицательное), то есть, по-прежнему, в сторону возрастания дуговой координаты.

Подставляя выражение (15) в формулу (14), получаем

(16)

Модуль вектора скорости равен V =| |. Когда > 0, вектор скорости направлен по вектору , когда < 0 , он имеет направление, противоположное вектору .

Величину часто называют алгебраической скоростью точки, считая ее проекцией вектора скорости на касательную к траектории точки.

29. Две основные задачи динамики точки:

1. Первая задача состоит в том, чтобы по заданному закону движения точки массой m определить силу, под действием которой происходит это движение. Часто первую задачу рассматривают как задачу управления движением, в рамках которой требуется установить характеристики воздействия, обеспечивающие заданный закон движения материальной точки. В зависимости от способа задания движения при решении этой задачи используют соответствующие скалярные уравнения.

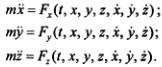(13.3)

2. Вторая задача состоит в определении движения точки по заданным силам и начальным условиям движения, при этом силы должны быть выражены как функции переменных, используемых для задания движения. Решение этой задачи сводится к интегрированию дифференциальных уравнений второго порядка, в процессе которого в решениях появляются произвольные постоянные, подлежащие определению. Так, в задаче о движении точки в трехмерном пространстве, решаемой на основе дифференциальных уравнений , общие решения будут содержать шесть произвольных постоянных:

,

для определения которых потребуется постановка дополнительных условий. Из математики известно, что если эти условия поставлены для начальных (при t = 0) значений функций и их первых производных, т. е. в виде x(0)=х₀, y(0)=у₀, z(0)=z₀, ,то задача (задача Коши) при некоторых ограничениях, налагаемых на правые части дифференциальных уравнений, имеет решение и причем единственное. Таким образом, приложенные к точке силы определяют только ее ускорение, движение же точки помимо сил зависит от начальных условий — положения точки в рассматриваемой инерциальной системе отсчета и ее скорости.

Две основные задачи динамики точки (из лекций):

1. Прямая: Зная m и действующую силу, определим движение материальной точки.

2. Обратная: Зная m материальной точки и ее уравнение движения, можно найти действующую на точку силу.