
- •4.Пара сил
- •Условия равновесия пар сил.
- •5.Законы Кулона
- •6.Скорости и ускорения точек тела при вращении.
- •11.Моменты инерции
- •12.Ускорение точки
- •1. Координатный способ задания движения
- •2.Ускорение точки при естественном способе задания движения.
- •15.Теорема об изменении кинетической энергии материальной точки.
- •Элементарный и полный импульс силы.
- •19. Сложение пар сил. Условие равновесия сил.
- •20.Динамические дифференциальные уравнения относительно движения материальной точки. Динамическая теорема Кориолиса
- •21.Разложение плоского движения твердого тела на поступательное и вращательное движение. Угловая скорость и угловое ускорение тела при плоском движении
- •22.Зависимость между моментами силы относительно оси и относительно любой очки лежащей на оси
- •23. Теорема о моменте равнодействующей силы (вариньона)
- •24. Построение и вычисление ускорения кариолиса
- •25. Аксиомы классической механики
- •26, Условия равновесия системы
- •Скорость точки
- •Нахождение скорости при естественном способе задания движения.
- •28. Скорость точки при векторном способе задания движения.
- •Определение скорости при координатном способе задания движения.
- •Нахождение скорости при естественном способе задания движения.
- •29. Две основные задачи динамики точки:
- •30. Кинетическая энергия системы.
- •31 Кинетическая энергия твердого тела.
- •33 . Дифференциальные уравнения сферического и свободного движений твердого тела
- •35) Условия равновесия в геометрической и аналитической формах.
- •Условия равновесия для частных случаев произвольной системы с ил в аналитической форме.
- •39) Теорема о скоростях точек плоской фигуры.
- •44)Приведение системы сходящихся сил к равнодействующей
- •Условия равновесия системы сходящихся сил
- •46.Поступательное движение твердого тела.
- •47.Дифференциальные уравнения движения материальной точки.
- •48.Теорема об изменении количества изменения точки
Нахождение скорости при естественном способе задания движения.
При движении точки по траектории радиус-вектор будет меняться с изменением дуговой координаты, а сама дуговая координата является функцией времени, то есть радиус-вектор является сложной функцией времени r = r (s(t)). По формуле (1) выразим вектор скорости точки:
|
(14) |
Рассмотрим
вектор dr
/ ds.
Согласно формуле (14), этот вектор направлен
по касательной к траектории, так как
скорость направлена по касательной, а
так как п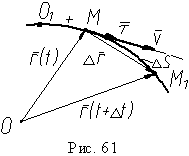 риΔs
0 предел
отношения длины дуги |Δs| к длине ее
хорды MM1 =
Δr (рис.
61) равен единице, то по модулю он равен
единице. Следовательно,
риΔs
0 предел
отношения длины дуги |Δs| к длине ее
хорды MM1 =
Δr (рис.
61) равен единице, то по модулю он равен
единице. Следовательно,
|
(15) |
где ![]() является
единичным вектором касательной к
траектории в точке M.
является
единичным вектором касательной к
траектории в точке M.
Вектор
всегда
направлен в сторону возрастания дуговой
координаты. На рис. 61 показан случай,
когда Δs
> 0 (дуговая
координата точки больше координаты
точки M1).
Сам вектор Δ![]() /Δs направлен
в сторону вектора Δ
,
в сторону положительного отсчета дуги.
Когда Δs
< 0 ,
точка M1 будет
находиться ближе к началу отсчета, чем
точка M,
вектор Δ
изменит
направление, а вектор Δ
/Δs будет
направлен в сторону, противоположную Δ
(Δs -
отрицательное), то есть, по-прежнему, в
сторону возрастания дуговой координаты.
/Δs направлен
в сторону вектора Δ
,
в сторону положительного отсчета дуги.
Когда Δs
< 0 ,
точка M1 будет
находиться ближе к началу отсчета, чем
точка M,
вектор Δ
изменит
направление, а вектор Δ
/Δs будет
направлен в сторону, противоположную Δ
(Δs -
отрицательное), то есть, по-прежнему, в
сторону возрастания дуговой координаты.
Подставляя выражение (15) в формулу (14), получаем
|
(16) |
28. Скорость точки при векторном способе задания движения.
Пусть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Т огда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:
|
(1) |
На рис. 59 изображено как определяется скорость точки. За приращение времени Δt точка переместилась по траектории из положения M в положение M1, а радиус-вектор получил приращение Δr. Когда Δt 0, точка M1 M, а вектор Δr, направленный по хорде MM1, стремится занять положение касательной к траектории. Поэтому вектор скорости V будет направлен, согласно выражению (1), вдоль касательной к траектории в точке M в сторону движения точки.
По определению, вектор скорости является скоростью точки в данное мгновение времени или мгновенной скоростью. Средней скоростью за промежуток времени Δt называется отношение Δr/Δt. Размерность скорости - м/с (метр в секунду), внесистемными единицами скорости могут быть см/с (сантиметр в секунду), км/час (километр в час) и т.д.
Определение скорости при координатном способе задания движения.
Пусть движение точки задано в декартовой системе координат Oxyz, которую считаем неподвижной, и известны кинематические уравнения движения точки: x = x(t); y = y(t); z = z(t). Используя равенство (5) в п. 26, по формуле (1) выражаем скорость точки:
Так как система координат Oxyz неподвижна, ее единичные векторы i,j,k постоянны (не меняют ни величину, ни направление), то слагаемые, содержащие производные этих векторов, равны нулю и
|
(9) |
Проекциями вектора скорости на оси координат являются сомножители перед единичными векторами, следовательно,
Зная проекции скорости на оси координат, можно определить величину вектора скорости:
|
(10) |
Направление вектора скорости определяется тремя направляющими косинусами:
|
(11) |
Формула (9) позволяет не только определить скорость аналитически, но и построить вектор скорости геометрически. По этой формуле вектор скорости можно представить как сумму трех взаимно перпендикулярных составляющих:
|
(12) |
где
|
(13) |
