26, Условия равновесия системы

Для равновесия твердого тела под действием произвольной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю:

1. Для плоской системы сил условие равновесия в аналитической форме имеет вид:

(6)

Таким образом, для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы проекций сил на оси координат и сумма алгебраических моментов всех сил относительно любой точки плоскости.

Выражения (6) являются основной формой условия равновесия для плоской системы сил. Существуют еще две дополнительные формы условий, которые мы сформулируем без доказательства.

I-я форма. Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю три суммы моментов сил системы относительно трех точек плоскости, не лежащих на одной прямой:

(7)

II-я форма. Для равновесия твердого тела под действием плоской системы сил необходимо и достаточно, чтобы равнялись нулю две суммы моментов сил системы относительно двух точек плоскости и сумма проекций сил системы на ось, не перпендикулярную прямой, соединяющей эти точки:

2. Для равновесия пространственной системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех прямоугольных осей координат были равны нулю и сумма моментов равна нулю.

27.

Скорость точки

Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета.

Скорость точки при векторном способе задания движения

Пусть движение точки относительно тела отсчета задано ее радиус-вектором r(t). Тогда, по определению, скоростью точки будет векторная производная радиус-вектора r по скалярному аргументу - времени t:

	(1)

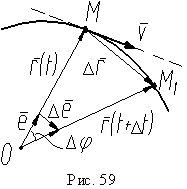
На рис. 59 изображено как определяется скорость точки. За приращение времени Δt точка переместилась по траектории из положения M в положение M₁, а радиус-вектор получил приращение Δr. Когда Δt   0, точка M₁   M, а вектор Δr, направленный по хорде MM₁, стремится занять положение касательной к траектории. Поэтому вектор скорости V будет направлен, согласно выражению (1), вдоль касательной к траектории в точке M в сторону движения точки.

По определению, вектор скорости является скоростью точки в данное мгновение времени или мгновенной скоростью. Средней скоростью за промежуток времени Δt называется отношение Δr/Δt. Размерность скорости - м/с (метр в секунду), внесистемными единицами скорости могут быть см/с (сантиметр в секунду), км/час (километр в час) и т.д.

Скорость точки при координатном способе задания движения

Пусть движение точки задано в декартовой системе координат Oxyz, которую считаем неподвижной, и известны кинематические уравнения движения точки: x = x(t); y = y(t); z = z(t). Используя равенство (5) в п. 26, по формуле (1) выражаем скорость точки:

Так как система координат Oxyz неподвижна, ее единичные векторы i,j,k постоянны (не меняют ни величину, ни направление), то слагаемые, содержащие производные этих векторов, равны нулю и

(9)

Проекциями вектора скорости на оси координат являются сомножители перед единичными векторами, следовательно,

Зная проекции скорости на оси координат, можно определить величину вектора скорости:

(10)

Направление вектора скорости определяется тремя направляющими косинусами:

(11)

Формула (9) позволяет не только определить скорость аналитически, но и построить вектор скорости геометрически. По этой формуле вектор скорости можно представить как сумму трех взаимно перпендикулярных составляющих:

(12)

где

(13)

Геометрически сложив составляющие, найдем вектор скорости. При построении составляющих по формулам (21) нужно учитывать: 1) если производная координаты положительна, то направление составляющей совпадает с направлением единичного вектора координатной оси; 2) если производная отрицательна, составляющая направлена в противоположную сторону.