1. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС МЕХАНИЧЕСКОЙ СИСТЕМЫ. Движение системы, кроме действующих сил, зависит также от её суммарной массы и распределения масс. Масса системы равна арифметической сумме масс всех точек или тел, образующих систему .

В однородном поле тяжести, для которого  , вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести:

,    ,    .                (1)

В полученные равенства входят только массы   материальных точек (частиц), образующих тело, и координаты   этих точек. Следовательно, положение точки С (x_C, y_C, z_C) действительно харак­теризует распределение масс в теле или в любой механической си­стеме, если под  ,  понимать соответственно массы и координаты точек этой системы.

Геометрическая точка С, координаты которой определяются указанными формулами, называется центром масс или центром инерции системы.

Положение центра масс определяется его радиус-вектором  , где   - радиус-векторы точек, образующих систему.

В ряде случаев для определения характера движения системы (особенно твердого тела), достаточно знать закон движения ее центра масс. Например, если бросить камень в цель, совсем не нужно знать как он будет кувыркаться во время полета, важно установить попадет он в цель или нет. Для этого достаточно рассмотреть движение какой-нибудь точки этого тела.

Чтобы найти этот закон, обратимся к уравнениям движения системы и сложим по­членно их левые и правые части. Тогда получим: .

Преобразуем левую часть равенства. Из формулы для радиус-вектора центра масс имеем: .

Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме произ­водных, найдем: или    .

где  - ускорение центра масс системы. Так как по свойству вну­тренних сил системы  , то, подставляя все найденные значения, получим окончательно:

                       (4)

Уравнение и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. Сравнивая с уравнением дви­жения материальной точки, получаем другое вы­ражение теоремы: центр масс системы движется как мате­риальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.

Центр масс механической системы движется как точка, масса которой равна массе всей системы M=Σm_i, к которой приложены все внешние силы системы: или в координатной форме:

где   - ускорение центра масс и его проекции на оси декартовых координат;  внешняя сила и ее проекции на оси декартовых координат.

2. Сложное движение точки - это движение точки, исследуемое одновременно по отношению к нескольким системам отсчета. Рассмотрим сложное движение точки М, перемещающейся по отноше-нию к подвижной системе отсчета O1X1Y1Z1, которая в свою очередь как-то движется относительно другой системы отсчета OXYZ, условно считаемой не-подвижной (рис. 1.73).

Движение точки М относительно подвижной сис-темы отсчета O1X1Y1Z1 называют относительным движением точки. Скорость и ускорение точки в относительном движении называют относительной скоростью и относительным ускорением, обозначают (  ,  ) Движение подвижной системы отсчета и неизменно связанного с ней тела по отношению к неподвижной системе отсчета OXYZ, называется переносным движением Переносной скоростью и ускорением точки называется абсолютная скорость и ускорение той неизменно связанной с подвижными осями точки, с которой в данный момент совпадает точка М (обозначают  ) Движение точки М относительно неподвижной системы отсчета OXYZ называется абсолютным или сложным движением. Скорость и ускорение точки в абсолютном движении называют абсолютной ( ) скоростью и абсолютным ускорением ( ). 

 (1.84) формула для нахождения скорости при сложном движении.

Теорема о сложении ускорений. Абсолютное ускорение, характеризующее изменение абсолютной скорости в абсолютном движении, найдем, продифференцировав по времени векторное равенство (1.84):

 (1.87)

1 группа - производные только от векторов  2 группа - производные только от относительных координат; 3 группа - производные от векторов и относительных координат Каждая из групп соответствует некоторому ускорению.

Переносное ускорение    - вычисляется, как если бы точка М покоилась по отношению подвижной системы осей (x1, y1, z1 = const) и перемещалась вместе с ними по отношению к неподвижной системе; - вычисляется, как если бы координаты x1, y1, z1 менялись, а векторы были постоянны. Последнее слагаемое называют п о в о р о т н ы м ускорением или ускорением Кориолиса - по имени французского ученого Г.Кориолиса

, используя формулы Пуассона  ;   ;   , получим  итак  (1.87)

Формула абсолютного ускорения точки в сложном движении принимает следующий вид:

Абсолютное ускорение точки в сложном движении равно геометрической сумме ее переносного, относительного и поворотного ускорений. 

3. Приведение системы сил к заданному центру.

Основная теорема статики (Пуансо). Любую произвольную систему сил, действующую на твердое тело, можно в общем случае привести к силе и паре сил. Этот процесс замены системы сил одной силой и одной парой сил называется приведением системы сил к заданному центру.

П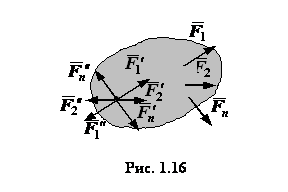 риведение плоской системы сил к данному центру. Теорема Пуансо

  Пусть к твердому телу приложена плоская система сил     (рис.1.16). Возьмем в теле произвольную точку   , ко­торую будем называть центром приведения, и приложим к ней по­парно уравновешенные силы     и   . Заметим, что силы     и   образуют при этом пару сил, так что можно считать силу     перенесенной параллельно самой себе в точку     - за­мененной силой     с присоединением пары  . Посту­пив так и со всеми оставшимися силами, мы приведем заданную систему сил к совокупности пучка сил   , приложенных в точке   , и совокупности пар   . Сходящиеся силы имеют равнодействующую   , приложенную в точке     и равную векторной сумме всех сил системы. Эта сумма называется главным век­тором системы и обозначается   .

 Пары можно заменить одной результирующей парой с моментом   , равным алгебраической сумме их моментов. Так как момент пары равен сумме момен­тов входящих в нее сил относительно любой точки плоскости пары, то для каж­дой из складываемых пар

 .

Поэтому сумма моментов пар равна сумме моментов самих заданных сил отно­сительно точки   , которая называется главным момен­том системы относи­тельно этой точки и обозначается   . Та­ким образом, систему сил, произ­вольно расположенных на плоско­сти, можно заменить совокупностью одной силы   , равной их главному вектору   , и приложенной в произвольно выбран­ном центре приведения, и одной пары, момент которой     равен главному мо­менту     заданных сил относительно центра приве­дения. Это утверждение на­зывается теоремой Пуансо о приведении плоской системы сил к данному цен­тру.

Главный вектор и главный момент системы опре­деляются по формулам:     ,   . (1.5)

4.Пара сил

Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Плоскостью действия пары сил называется плоскость в которой расположены эти силы.

Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.

Моментом пары сил называется вектор , модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия сил пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.

Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.

Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.

Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.

Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.

Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.

Теорема о сложении пар сил. Две пары сил, действующих на одно и то же твердое тело, и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Условия равновесия пар сил.

Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.

Теорема. Для равновесия пар сил, приложенных к твердому телу, необхо-димо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.

Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.

5.Законы Кулона

1. Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Сила трения зависит от активных сил, и её модуль заключён между нулём и максимальным значением, которое достигается в момент выхода тела из положения равновесия, то есть:

- называется предельной силой трения.

2. Предельная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того чтобы сдвинуть, например кирпич, надо приложить одну и туже, силу, независимо, от того, какой гранью он положен на поверхность, широкой или узкой.

3. Предельная сила трения скольжения пропорциональна нормальной реакции (нормальному давлению), то есть

,

где безразмерный коэффициент называют коэффициентом трения скольжения; он не зависит от нормальной реакции.

4. Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, то есть от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения устанавливается экспериментально.

Считается, что коэффициент трения не зависит от скорости движения.