15.Выбор между явными и неявными методами в процедурах моделирования мехатронных с-м (их достоинства и недостатки)

Неявные методы лучше приспособлены для решения систем диф. и алгебраических уравнений, к тому же они более устойчивы. В рез-те, несмотря на большие затраты машинного времени на каждом шаге интегрирования, связанные с необходимостью решения с-м лин. алгебраических ур-ний, общ. затраты м.б. знач-но меньше за счет увеличения шага интегрирования и уменьшения общего кол-ва шагов.

Рассмотрим эту особенность.

.

Применим указанные формулы для численного интегрирования простейшего лин. ДУ:

.

Характеристическое уравнение данной динамической системы имеет вид , или , где – постоянная времени системы.

Разностное ур-ие, соответствующее численному решению явным методом Эйлера, запишется как

.

Условие уст-ти полученного ур-ия: или . .

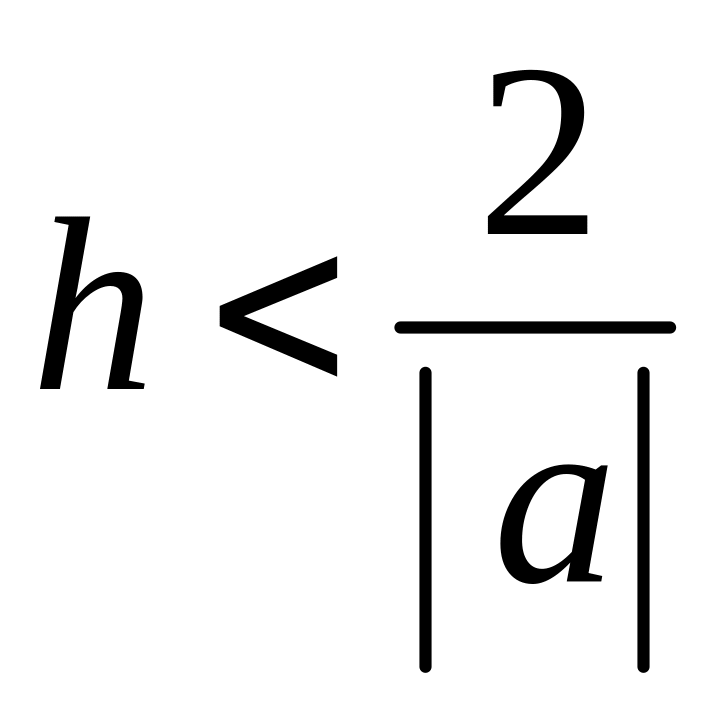Для метода Рунге-Кутты 4-го порядка требование устойчивости ограничивает шаг величиной 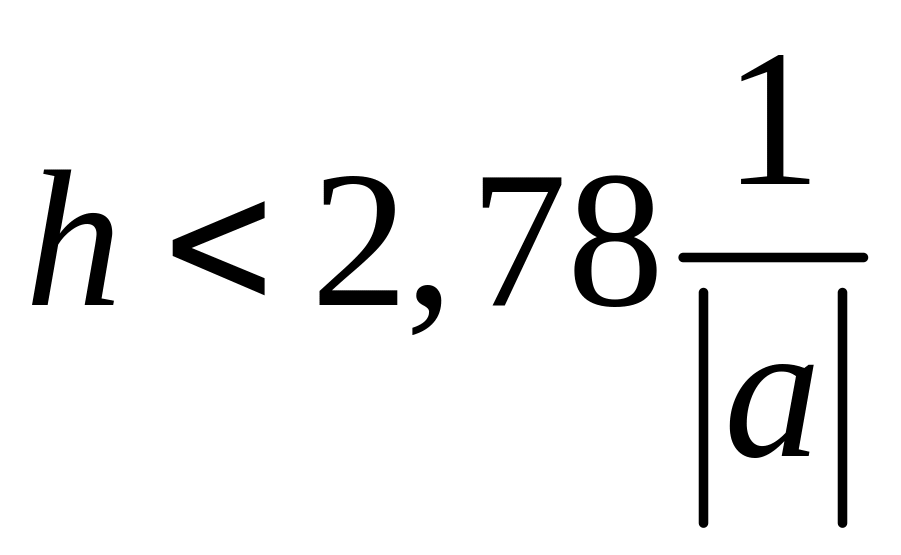, или, в более общем виде, , где – макс. Собств. значение матрицы Якоби.

Применение неявного метода Эйлера к той же системе дает

,

где ограничение на величину шага выглядит по другому: , что позволяет выбрать шаг любой величины, ориентируясь только на требуемый уровень погрешности.

Подготовка ДУ к численному интегрированию

Реальные мехатронные объекты и мехатронные системы описываются, как правило, системами нелинейных алгебраических и дифференциальных уравнений. Для большинства задач, представляющих практический интерес, решение их аналитическими методами невозможно. Результаты могут быть получены путем построения приближенных решений с помощью численных методов интегрирования, в частности конечно-разностных методов.

Общая идея численного интегрирования обыкновенного дифференциального уравнения (ОДУ) заключается в том, что производится дискретизация независимой переменной - времени на интервале и замена ее рядом значений (принцип ). Расстояние между двумя соседними значениями называется шагом интегрирования. В частном случае он может быть постоянным на всем заданном интервале изменения переменной . В результате, системе дифференциальных уравнений тем или иным способом ставится в соответствие система конечно-разностных уравнений

,

где – некоторая вектор-функция, определяемая способом построения метода; – количество предыдущих точек, которые используются в методе интегрирования.

Процедура интегрирования предполагает решение полученной системы конечно-разностных уравнений для фиксированных моментов времени , начиная с момента , для которого определено начальное состояние исследуемой системы . Соответственно, решение получается в виде совокупности значений для заданных моментов времени.

16.Многошаговые методы интегрирования

Методы, зависящие только от и не использующие никакие предыдущие значения переменной называются одношаговыми и могут быть представлены в общем виде как с соответствующей функцией . Можно добиться большей точности, если использовать инф-цию о неск-ких предыдущих точках Именно так поступают в многошаговых методах.

Задача Коши: Если подставить в приведенное ДУ точное решение и проинтегрировать на отрезке , то получим 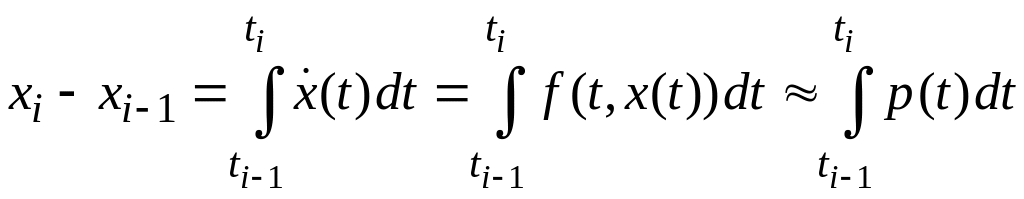, где - полином, аппроксимирующий . Чтобы записать этот полином, предположим, как обычно, что – приближения к решению в точках и узлы расположены равномерно с шагом . Т.о., – полином степени , удовлетворяющий условиям Этот полином можно явно проинтегрировать, что ведет к методу .

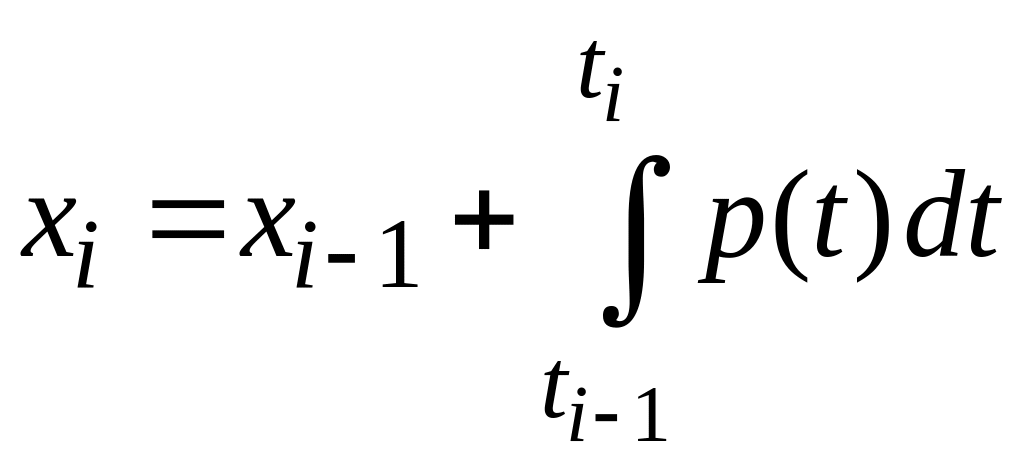Для , полином есть константа, равная , и мы получаем обычный метод Эйлера. Если , то – линейная функция, проходящая через точки и , т.е.

Интегрируя ее от до , получаем следующее выражение: , которое соответствует двухшаговому методу интегрирования, поскольку использует информацию в двух предыдущих точках. Аналогично, если , то является квадратичным полиномом, а соответствующий трехшаговый метод имеет вид

Эти методы наз-ся методами Адамса-Бишфорта.

Многошаговые методы порождают проблему, которая не возникала при использовании одношаговых методов. Интегрирование начинается с начального значения , но при необходима информация о значении функции в точках , которая отсутствует. Обычный выход из положения состоит в использовании какого-либо одношагового метода того же порядка точности, пока не будет набрана необходимая информация.

Многошаговыми м.б. и неявные методы. В этом случае в ф-лы входят зн-ния , которые могут быть определены только неявно, и найдены в рез-те решения с-мы алгебраических Ур-ний. Методы этой группы обычно наз-ся методами Адамса-Моултона.