13.Варианты Data Flow и Control Flow управления процессом структурного моделирования

Структурное модел-ние предусматривает 2 варианта управления п-сом моделирования:

• поток команд (Control Flow),

• поток данных (Data Flow).

П-п потока команд – это обычный п-п записи программ в текстовых языках программирования, где инструкции вып-ся в той послед-ти, в к-ой они написаны. Если в п-се выполнения очередной инструкции программа обнаруживает, что какие-то данные не определены, это рассматривается как ошибка и влечет за собой остановку программы.

Жесткие формы языков программирования, на основе к-ых формируется моделирующая программа при использ-нии п-па Control Flow, плохо сочетаются с возрастающим уровнем граф, языков. При любой форме задания графической инф-ции ее необходимо преобразовать в выполняемые инструкции, т.е. послед-ть команд для процессора, т.к. код граф, языка не может выполняться "строка за строкой". Это ведет к необходимости автоматически преобразовывать введенные пользователем или построенные графическим интерфейсом уравнения к формам, с которыми могут работать, например, библиотеки программных реализаций численных методов.

В этом случае эффективной явл-ся технология потока данных (Dataflow). САМ, работающая на поточной технологии управления процессом моделирования, обязательно содержит блок, упорядочивающий поток данных (информационный поток).

Технология потока данных – с-ма программирования, состоящая из исполняемых узлов данных. Узлы выполняются только тогда, когда все необходимые данные поступят на их входы.

14. Классификации методов численного интегрирования:

• методы явные и неявные;

• методы одношаговые и многошаговые;

• методы первого, второго и т.д. порядков;

• методы с постоянным шагом и методы с автоматическим выбором шага

Методы явные и неявные

Е сли задано диф. ур-е (3.1) и начальные условия , то очередное значение : 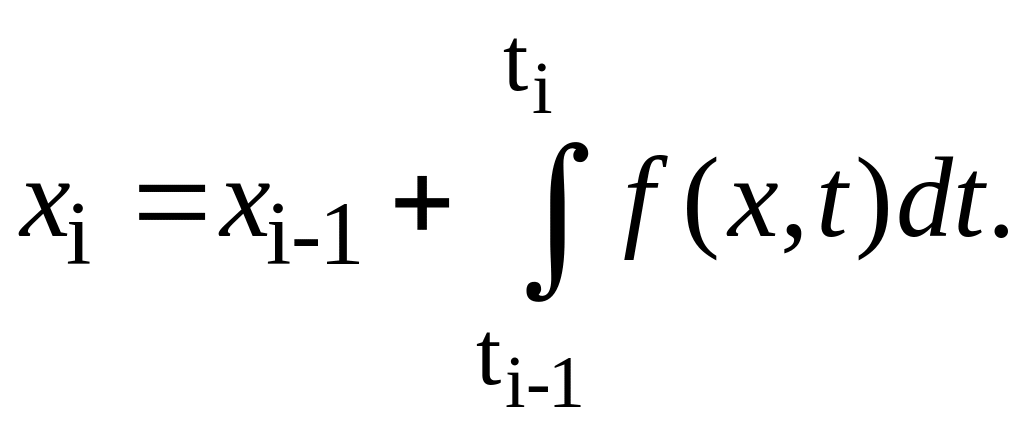Опр. интеграл численно = площади под кривой на интервале . Приближенно эта площадь м.б. вычислена как площадь прямоуг-ка, высота к-го = зн-нию ф-ции на левой границе интервала или зн-нию на правой границе.

(3,3) явн метод. Неизвестное значение м.б. непосредственно вычислено по известному значению в предыдущей точке.

. не явн метод. Здесь в правой части выражения исп-ся неизвестное зн-ие , поэтому вычислить его непосредственно по этой ф-ле нельзя.

Более точное значение интеграла дает метод трапеций, к-му соответствует отрезок 3. Тогда .

Для явных процедура форм-ния модели для числ. интег-ния огранич-ся алгебр-цией исх. диф.ур-й.

Для неявн. методов дальнейшие д-вия зав-ят от того, какой метод решения с-мы нелин. ур-ий реализован в данном пакете. Этап подготовки мат. моделей для неявн. методов, к-ый состоит в линеаризации нелин. алгебраических ур-ий, т.е. в разложении нелин. ф-ий в р.Тэйлора

Пусть задано нелинейное алгебраическое уравнение где - вектор переменных.

Разложение в ряд Тэйлора:

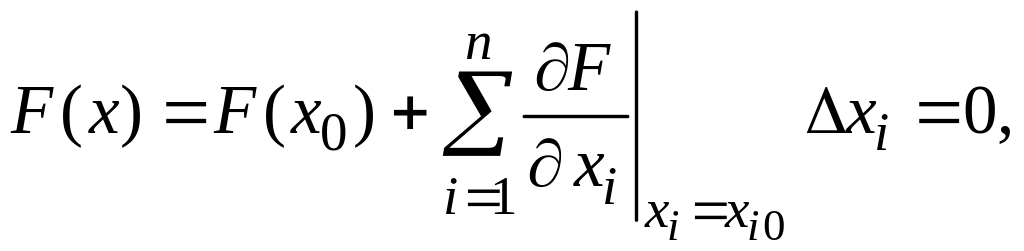где – нач. приближение, в кач-ве к-го берутся зн-ния переменных на предыд. шаге интег-ния; ; – неизв. зн-ние переменной на шаге интег-ния. м.б. записано как лин.алг. ур-ие:

, где ,

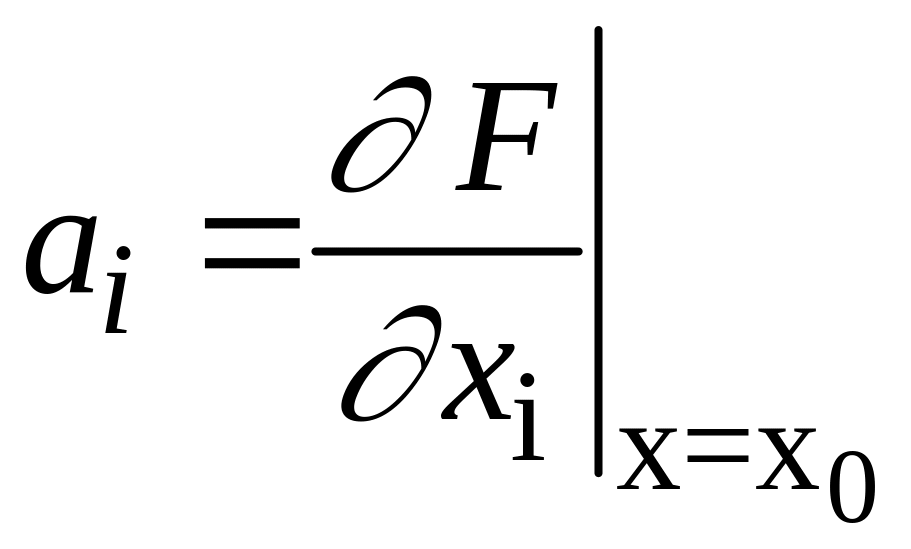Т.о., п-с числен. модел-ния в общ. случае нелин. с-м неявн. методами состоит в форм-нии и решении на каждом шаге интег-ния с-мы лин. алгебр. ур-ий : к-ая вкл-ет компонентн. и топологич. ур-ния моделируемой схемы.