6. Аналитическое моделирование. Методы исследования аналитических моделей.

Для аналит. мод-ния характерно то, что процессы функц-ия элементов системы зап-ся в виде некоторых функцион. соотношений (алгебр., интегро-диф., конечно-разностных и т.д.) или лог. условий. Методы исследования аналит.моделей: аналитический (стремятся получить в общем виде явные завис-ти для искомых характ-к ;численный (не умея решать ур-я в общем виде, стремятся получить числ. результаты при конкр. нач. данных; качественный ( не имея решения в явном виде, можно найти некоторые св-ва решения (ex: оценить устойчивость).

Наиболее полное исслед-е процесса функц-ния можно получить, если известны явные зав-ти, связ. искомые характ-ки с нач. усл., параметрами и переменными исслед. системы, т.е. в результате аналит. решения задачи. Однако такие завис-ти удается получить только для простых систем. Численный метод позволяет иссл-ть, более широкий класс систем, но получ. решения носят частный характер. При иссл-нии сложных систем наиболее эффект. явл-ся методы имитац. мод-ния.

7. Имитационное моделирование. Достоинства и недостатки. Критерии целесообразности применения.

Имитац. мод-ние - мод-ние, при кот. реализующий модель алгоритм воспроизводит процесс функц-ния системы во времени, причем имитируются элементарные явл-я, составл. процесс, с сохранением их лог. структуры и последов-сти протекания во времени. В этой модели сохранены и легко узнаваемы такие черты моделируемого объекта, как структура, связи м/у компонентами, способ передачи инф-ции. + возможность решения более сложных задач. Имит. модели позволяют достаточно просто учитывать наличие дискр. и непрерыв. эл-тов, нелин. харак-ки эл-тов, случ. возд-вия и т.д. -: решение, полученное методом имитац. мод-ния, всегда носит частн.характер, для полного анализа приходится многократно воспроизводить имитац. эксперимент, изменяя исх. данные. Издержки, связ. с имитац. мод-ем, всегда намного выше, чем при аналит. исслед-ях.

Основные критерии целесообразности применения: отсутствие законченной матем. постановки задачи, не разработанность методов ее аналит. решения либо их чрезмерная сложность и трудоемкость, слабая подготовка персонала, не позвол. ими воспользоваться, если иных методов решения задачи просто нет, либо требуется сущ-ное "сжатие" по времени.

8. Особенности управления и моделирования систем с распределенными параметрами. Общая формулировка закона сохранения.

Сущ-ют системы, состояние кот. ха­ракт-ся поведением во вр. некот. набора конечного числа ф-ий одной переменной : .Подобные системы описываются обыкн. ДУ относительно и наз-ся системами с сосредоточенными параметрами (ССП).

Особенность ССП: описание управляемых процес­сов в терминах величин, не отражающих в явной форме влияние про­странственной протяженности объекта на его характеристики.

Т.к. на практике любой техн. объект упр-ния имеет вполне определ. геом. размеры, то ф-ия, характ-щая его состояние зависит не толь­ко от времени, но и от вектора простран. координат, являясь функцией Q(x,t) no меньшей мере двух аргументов. Здесь приходится иметь дело с бескон. числом управляемых величин (по числу точек в рассматр. про­странств. области) , каждая из кот. харак-ет поведение объекта в соотв. фиксир. точке х. Такие системы, состояние кот. опис-ся ф-ями несколь­ких аргументов, зав. как от врем., так и от простран. координат, наз-ся системами с распределенными параметрами (СРП).

Практически любой реал. объект упр-ния предст. собой СРП, и лишь в частных случаях его можно с некоторыми допущениями и погрешностями отнести к типу ССП.

Задачи упр-ния СРП более сложные в сравн. с ССП ввиду целого ряда принцип. особ-тей:

1. состояние сист с распределёнными параметрами зависит как от времени, так и от пространственных ординат и описываются уравнениями частных производных.

2. по сравнению с системами с сосредоточенными параметрами расширяется класс управляющих воздействий за счёт включения пространственно-временных управлений.

3. задача реализации систем управления объектами с распределёнными параметрами резко усложняется по сравнению с системами с сосредоточенными параметрами за счёт необходимости осуществления пространственно временного контроля состояния объекта и введения соответствующих обратных связей.

Для постр-ния мат моделей тех. объектов с распред. парам. классич. методом исп-ся фундам. физ. законы: сохр-я энергии, массы, момента. На их основе строятся ур-ния баланса.

О бщая формулировка закона сохранения: изм-ние во вр. некоторой субстанции в элементарном объёме равно сумме притока-стока ч/з его поверхность с учётом скорости генерации или уничтожения субстанции в этом объекте.

φ – фазовая переменная

Ј – векторы плотности потока фазовой переменной

G – скорость генерации(уничтожения) субстанции в объеме

Div J – скалярная функция заданного аргумента. 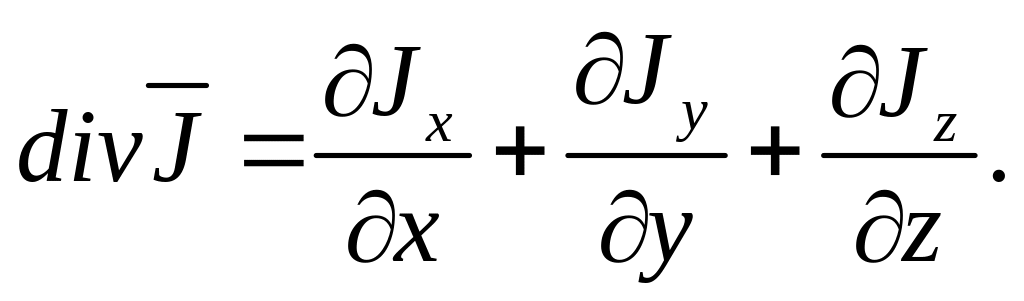Дивергенция вектора плотности потока характ-ет сумму притока-стока субстанции ч/з повер-сть элемент. объема.

Уравнение закона сохранения энергии : , где - - энергия ед-цы объема; - вектор плотности потока энергии; - скорость генерации или поглощения энергии в единице объема.