образования и науки РФ

ГОУ ВПО МО

Московский государственный областной социально-гуманитарный институт

Курсовой проект

по сопротивлению материалов

Тема: расчет стержневых систем на прочность

и жесткость

Выполнил: студент

Технологического факультета

Группы

Руководитель:

Тимошин Ю.Н.

Коломна 2011

Задача №1

Для чугунного статически определимого бруса переменного поперечного сечения требуется:

- построить эпюру продольных сил;

- из расчета на прочность определить площади поперечных сечений участков при заданном их соотношении;

- построить эпюры нормальных напряжений и перемещений;

Вариант № 1

Схема варианта

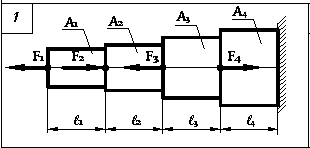
Данные варианта

Для решения задачи определим величины нагрузок в сечениях балки.

Зависимость определяется по формуле

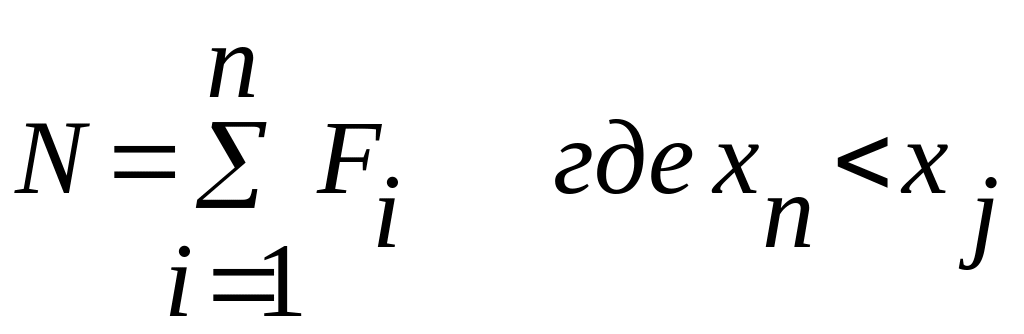
Где xj – текущее значение координаты балки начиная с левого торца

Зависимость имеет следующий вид:

X(см)	FN(кН)
0	-50
50	-50
50	10
115	10
115	70
185	70
185	40
270	40

Эпюра продольных сил представлена на рисунке 1

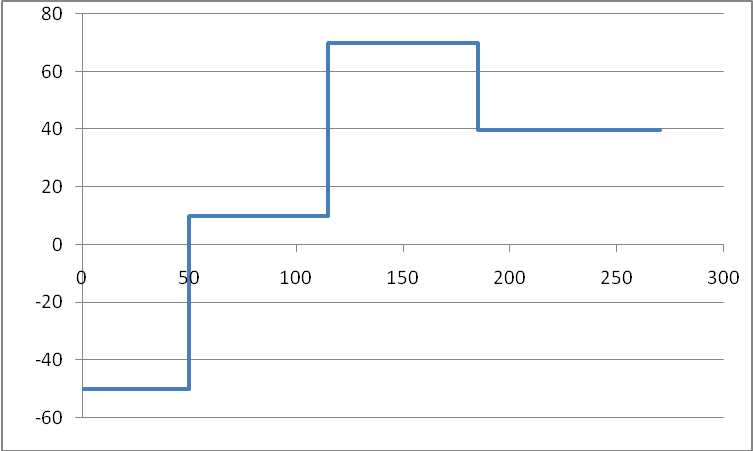
Рис 1

Зависимость напряжений при А=1 м² представлена в таблице

x		Sx
0		-50
50		-50
50		8,333333
115		8,333333
115		38,88889
185		38,88889
185		20
270		20

Находим максимальные значения напряжений

Видим, что критическим является деформация растяжения, поэтому площадь считается по этой деформации

Арас(см2)

10

Зависимость нормальных напряжения и деформаций представлены в таблице

x			т		p
0			-50		0,012319
50			-50		0,024819
50			8,333333		0,024819
115			8,333333		0,022111
115			38,88889		0,022111
185			38,88889		0,0085
185			20		0,0085
270			20		0

Эпюры напряжений и деформаций представлены на рисунках 2-3

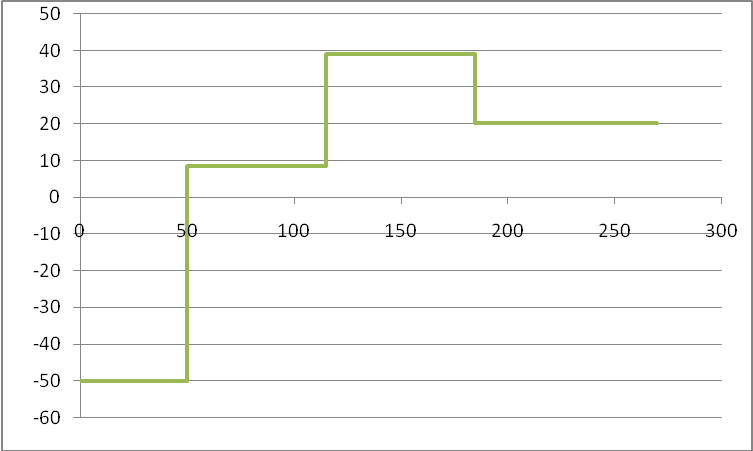
Рис. 2

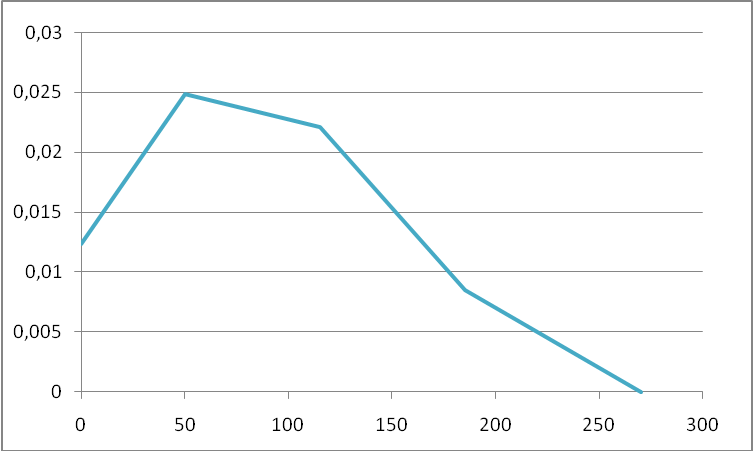
Рис 3

Задача №2

Для стального статически неопределимого бруса переменного поперечного сечения требуется:

- раскрыть статическую неопределимость;

- построить эпюру продольных сил

- из расчета на прочность определить площади поперечных сечений участков;

- построить эпюры нормальных напряжений и перемещений;

- проверить жесткость бруса, приняв допускаемое значение абсолютной продольной деформации [Δl]=2,5мм.

Отношение площадей A1:A2:A3=1:1.2:1.5

Данные для расчета взять из таблицы 2 в соответствии с заданным номером схемы и номером варианта рассчитываемого бруса.

Пример решения задачи.

Схема варианта

Для раскрытия неопределенности вычислим деформации левого торца при предположении, что А = 1 м2 а σ =1 Па тогда деформации вызванные действием сил F1 и F2 ,будут иметь вид:

F2	240
F1	525

Деформация левого торца, вызванная действием силы реакции в нем при единичной величине реакции будет

R	155

Уравнением совместимости деформаций в данном случае будет равенство нулю суммарной деформации в левом торце.

То есть ΔλR+ ΔλF1+ ΔλF2=0

Следовательно R = -4,93548

Таким образом статически неопределимая схема приводится к схеме на рис. 4

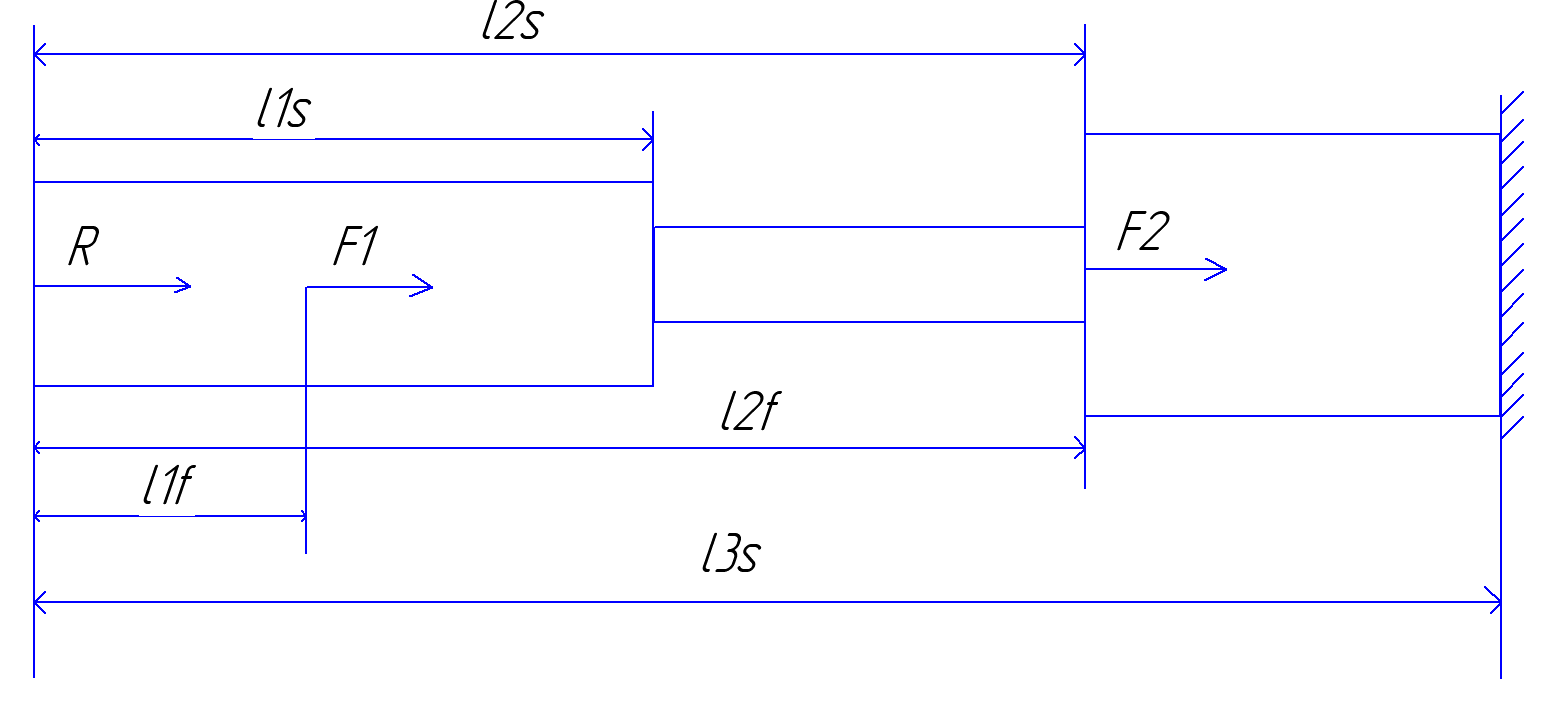
Рис 4

Определим величины нагрузок в сечениях балки.

Зависимость определяется по формуле

Где xj – текущее значение координаты балки, начиная с левого торца

Зависимость имеет следующий вид:

xs FN 190 8,064516 145 8,064516 145 0,064516 145 0,064516 145 0,064516 120 0,064516 120 0,064516 60 0,064516 60 -4,93548 0 -4,93548

Эпюра продольных сил представлена на рисунке 5

Рис 5

Зависимость напряжений при А=1 м² представлена в таблице

xs	FN	Sig(0)
190		5,376344
145		5,376344
145		0,043011
145		0,064516
145		0,064516
120		0,064516
120		0,053763
60		0,053763
60		-4,1129
0		-4,1129

Находим максимальные значения напряжений и площадь обеспечивающую прочность балки

SigMax

5,376344

A(см2)

0,268817

Зависимость нормальных напряжения и деформаций представлены в таблице

xs							(см)
190					200	0,000952	0
145					200	0,000952	0,042857
145					1,6	7,62E-06	0,042857
145					2,4	1,14E-05	0,042857
145					2,4	1,14E-05	0,042857
120					2,4	1,14E-05	0,043143
120					2	9,52E-06	0,043143
60					2	9,52E-06	0,043714
60					-153	-0,00073	0,043714
0					-153	-0,00073	0

Эпюры напряжений и деформаций представлены на рисунках 6-7

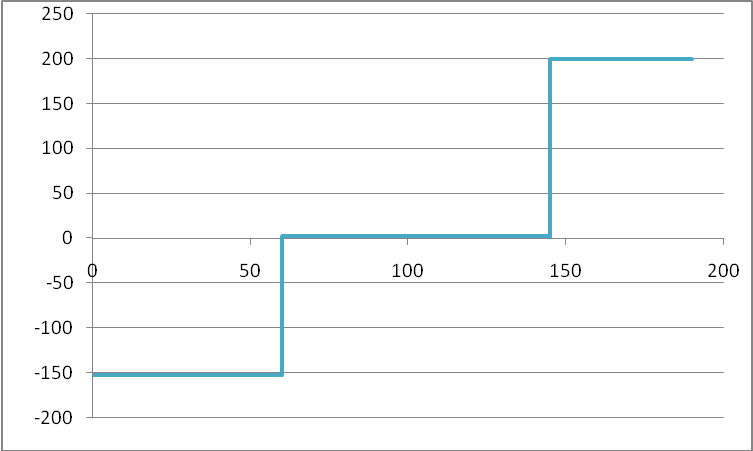
Рис. 6

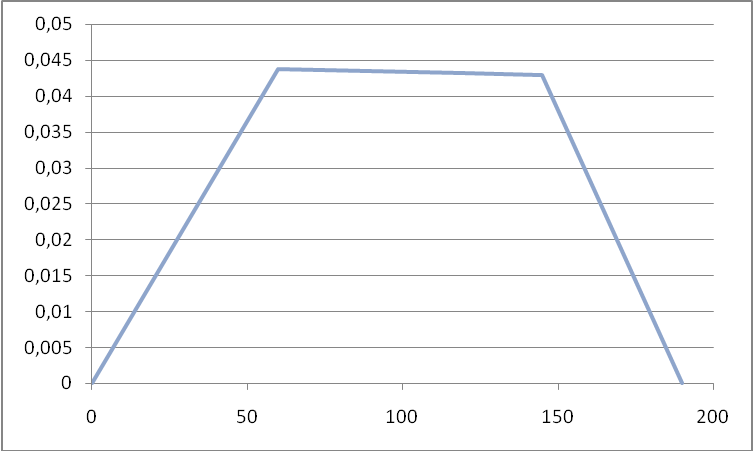
Рис 7

Как видим деформации стержня не превышают 0,5 мм, то есть балка является устойчивой.