Моделирование системы регулирования по отклонению
Модель системы регулирования по отклонению создана с помощью языка программирования Pascal в среде разработки Delphi 7.
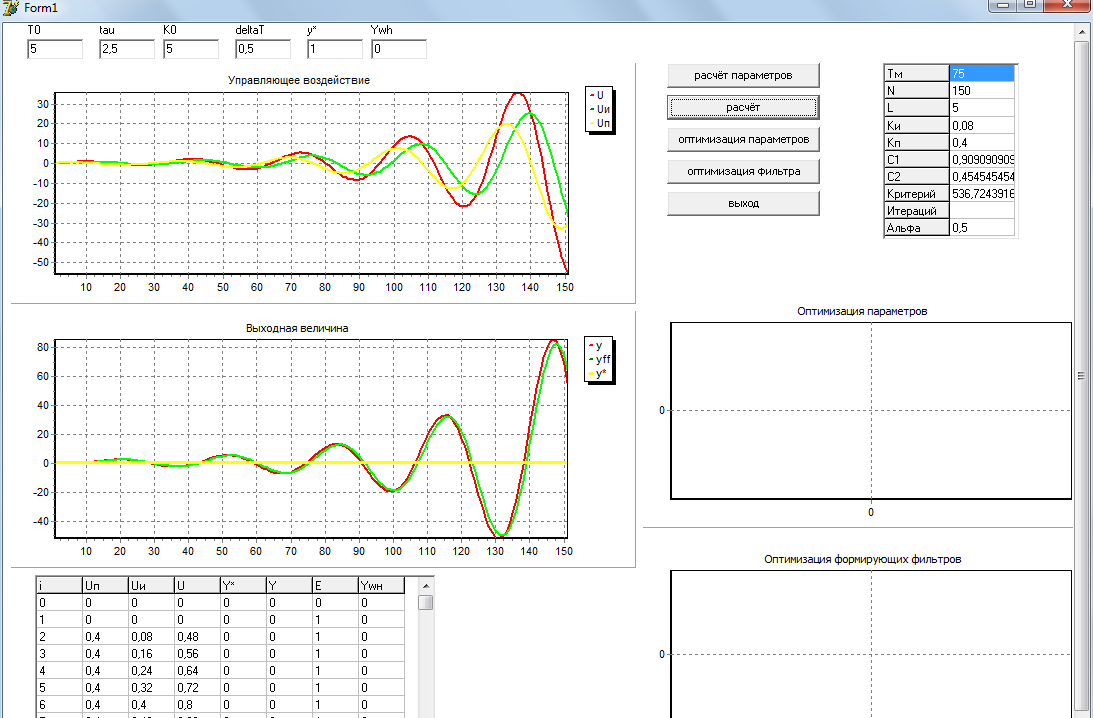
Рисунок 5 – Расчёт параметров
Начальные
значения для моделирования системы
регулирования по отклонению:
=5,
τ=2,5, k0
=5, y*=1,
ywн
=0.1* Y*.
Настроечные параметры регулирования kп =0,4 и kи =0,08
Смоделированный выходной сигнал отклоняется от требуемого значения, следовательно настроечные параметры не удовлетворяют условиям задачи.
Проведем оптимизацию с помощью метода покоординатного спуска.
Поиск оптимальных настроек регулятора модели системы регулирования по отклонению методом покоординатного спуска.
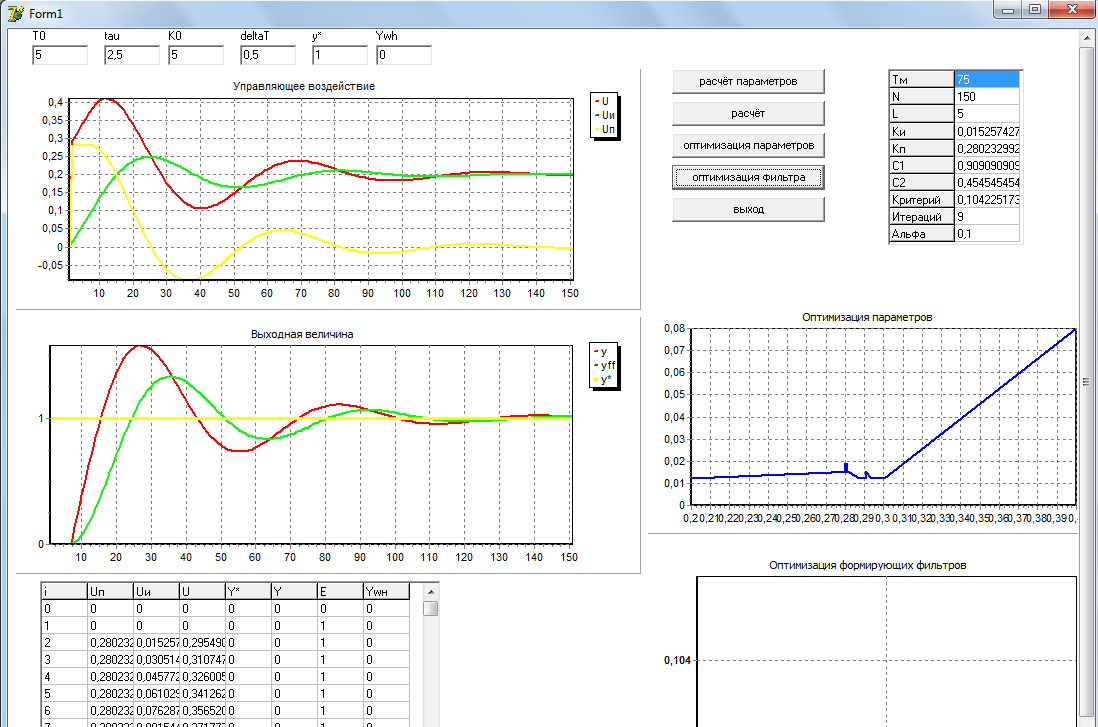
Рисунок 6 - Моделирование системы регулирования по отклонению с оптимизированными настроечными параметрами.
После проведенной оптимизации параметров мы получили настроечные параметры kп =0,28 и kи=0,015. Среднеквадратический критерий при этом стал равен 0,104. Так же по графику из рисунка 6 отчетливо видно, что смоделированный выходной сигнал приближается к заданию, но с некоторой погрешностью. Применим к неконтролируемому воздействию формирующий фильтр и оптимизируем настроечный параметр α методом полного перебора.
Поиск оптимальных настроек формирующего фильтра системы регулирования по отклонению методом покоординатного спуска
Оптимизировав настроечный параметр, мы получили α=0,1. Именно это значение α является оптимальным, при котором выходная величина наиболее точно стремится к заданию.
Оценим
влияние формирующего фильтра на
неконтролируемое входное воздействие
при моделирование системы регулирования
по отклонению. Для этого возьмем 4
различных значения
:
ywн =0* y* (0% от задания);
ywн =0,33* y* (33% от задания);
ywн =0,66* y* (66% от задания);
ywн =0,1* y* (100% от задания);
Оценим результаты моделирования во всех 4х случаях.
Проанализировав полученные данные, была выявлена зависимость α от : чем больше неконтролируемое возмущение, тем меньше настроечный параметр. Отсюда следует, что при малых значениях формирующий фильтр не требуется, потому как из-за него возрастает среднеквадратический критерий, однако при больших необходим фильтр с малым значением настроечного параметра α.
Исследование влияния отношения транспортного запаздывания к времени спада АКФ на величину среднеквадратического критерия
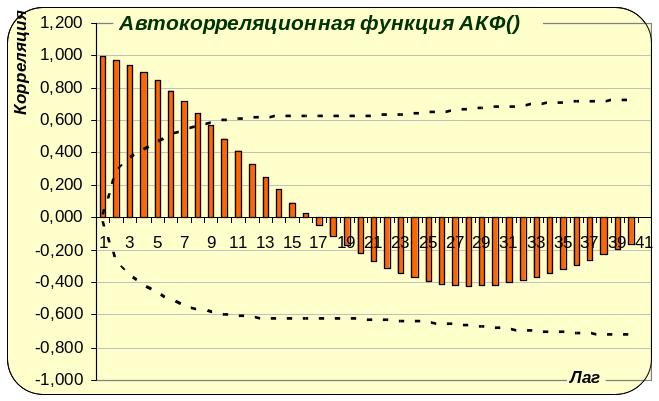
Время спада АКФ Такф=16.
Критерий |
тау/АКФ |
тау |
0,069 |
0,15625 |
2,5 |
0,057 |
0,1 |
1,6 |
0,094 |
0,5 |
8 |
0,1 |
0,75 |
12 |
0,104 |
1 |
16 |