2.2 Индуктивность. Катушка индуктивности

Индуктивность – идеальный двухполюсный элемент, в котором накапливается энергия магнитного поля (рисунок 5). Введение в теоретическое рассмотрение индуктивности позволяет описывать процессы, связанные с возникновением магнитного потока в каком-либо участке цепи, например при протекании тока по проводу катушки индуктивности.

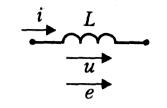
Рисунок 5

Простейший вариант катушки индуктивности – изолированный провод, намотанный на каркас (сердечник), который изготавливают из диэлектрика или ферромагнитного материала. Протекающий по катушке индуктивности ток i связан с полным магнитным потоком, или (другое именование) с потокосцеплением самоиндукции , следующим соотношением:

 = Li.

Эта формула записана при таком выборе направления отсчета тока и магнитного потока, при котором знаки тока и потокосцепления одинаковы. Следовательно, L > 0. Параметр (коэффициент) L называется, как и сам элемент, индуктивностью. Коэффициент L для линейной индуктивности не зависит от тока или потокосцепления. В дальнейшем рассматриваются только линейные и не зависящие от времени индуктивности.

Изменение тока во времени влечет изменение полного магнитного потока, пронизывающего витки катушки индуктивности. Согласно закону электромагнитной индукции изменяющийся магнитный поток возбуждает вихревое электрическое поле, и на выводах катушки индуктивности (а значит, и на полюсах индуктивности) появляется электродвижущая сила самоиндукции:

е = – d/dt.

ЭДС самоиндукции противодействует изменению потокосцепления, а, следовательно, и тока в индуктивности. При совпадающих условных положительных направлениях i и е это «противодействие» учитывается знаком «минус» в формуле. Напряжение на индуктивности и при указанных на рисунке 5 опорных направлениях равно – е и в случае линейной и неизменной во времени индуктивности пропорционально скорости изменения протекающего через индуктивность тока i. Связь тока и напряжения на индуктивности выражается формулами:

В реальных цепях недопустимы мгновенные изменения магнитного потока, и это означает, что ток, протекающий через неизменную во времени индуктивность, является непрерывной функцией – он не может меняться скачком.

Единица измерения индуктивности – генри. Сокращенное обозначение – Гн (в России) или Н (международное обозначение).

Чтобы реализовать требуемую индуктивность, в цепь включают подходящую катушку индуктивности. Предположим, что катушку индуктивности изготовили, намотав  витков изолированного провода на магнитопроводящий сердечник, или магнитопровод, характеризуемый относительной магнитной проницаемостью . (При необходимости на схемах указывают наличие магнитопроводящего сердечника в катушке индуктивности; пример приведен на рисунке 6, а.) Индуктивность катушки с сердечником вычисляют по формуле

L =  ₀ S ²/ l,

в которой: ₀ = 4 10 ^-7 Гн/м – магнитная постоянная, S — площадь поперечного сечения сердечника, l – средняя длина сердечника. Эта формула годится и для тороидальной (рисунок 6, б), и для цилиндрической (рисунок 6, в) катушки при условии, что длина цилиндра в 3-4 раза больше диаметра поперечного сечения цилиндра.

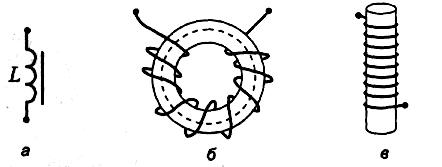
Рисунок 6

При описании электрических свойств катушки индуктивности бывает недостаточно учитывать только индуктивность L. Часто приходится считаться с потерями в проводе. Поэтому последовательно с индуктивностью L в схему замещения катушки индуктивности включают сопротивление потерь r₀ (рисунок 7, а). Его приходится учитывать, если на рабочей частоте нарушается неравенство 2fL >> r₀. Такое может случиться еще на относительно низких частотах, например, при наматывании катушки длинным и тонким проводом.

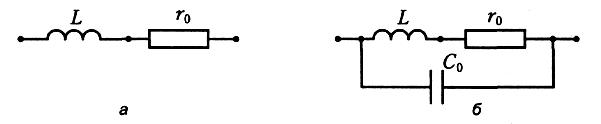
Рисунок 7

При вычислении сопротивления потерь r₀ надо иметь в виду, что оно отличается от сопротивления постоянному току вследствие поверхностного эффекта, или скин-эффекта, – неравномерного распределения переменного тока по поперечному сечению проводника. Из-за скин-эффекта плотность тока оказывается максимальной вблизи поверхности и минимальной на оси провода. Чем выше частота колебаний, тем сильнее эта неравномерность выражена – на очень высоких частотах ток в основном течет в тонком поверхностном слое (в скин-слое). В результате уменьшается эффективная площадь поперечного сечения провода. Известно, что с ростом частоты сопротивление провода увеличивается пропорционально корню квадратному частоты. Неравномерность распределения тока в проводе катушки дополнительно усиливается за счет того, что он свернут в виток и около него расположены другие витки (проявляется эффект близости).

На высоких частотах начинают заметно проявляться токи смещения, замыкающиеся между витками катушки. Для их учета в схему замещения вводят емкость С₀, подключая ее параллельно индуктивности и сопротивлению (рисунок 7, б).