3.6 Протокол g.703 Семенов ю.А. (гнц итэф)

(ITU-T Recommendation G.703.Physical/Electrical Characteristics of Hierarchical Digital Interfaces. 1972 last amended in 1991).

Интерфейс G.703 (ITU-T Recommendation G.703.Physical/Electrical Characteristics of Hierarchical Digital Interfaces. 1972 last amended in 1991) был разработан в 1972 году и базируется на стандартах G.702, G.704 и I.430 и обслуживает сети с иерархией PDH и SDH. Первоначально он разрабатывался для систем с импульсно-кодовой модуляцией. G.703 может работать на скоростях передачи данных 64 Кбит/с, 1544, 6312, 32064 и 44736 Кбит/с (PDH, американская версия), 2048, 8448, 34368, 139264 Кбит/с (европейская версия). Предусматривается работа и при 155,52 Мбит/с. В качестве физического канала передачи может использоваться скрученная пара (Z=100-120 Ом) или коаксиальный кабель (75 Ом), амплитуда импульса 1-3В.

При скорости 64 Кбит/с через интерфейс передается три типа сигналов: информационный (64 Кбит/с) и два синхронизирующих тактовых 64 Кбит/с и 8 Кбит/с. Стандарт предусматривает 3 вида взаимодействия терминального оборудования: однонаправленный (codirectional; рис. 3.6.1), разнонаправленный (рис. 3.6.2) и с центральным тактовым генератором (рис. 3.6.3).

Рис. 3.6.1. Однонаправленная передача информации и тактовых сигналов

Рис. 3.6.2. Разнонаправленная передача информации и тактового сигнала для 64 Кбит/с

Во втором варианте терминалы неравноправны - один из них управляющий, другой - управляемый. Тактовые сигналы идут в этом случае только от управляющего терминала.

Рис. 3.6.3. Интерфейс с центральным тактовым генератором для 64 кбит/с

Частота синхронизирующих сигналов может быть меньше скорости передачи данных в 2, 4 и 8 раз. Тип кода зависит от скорости передачи и типа аппаратного интерфейса. Характеристики основных разновидностей интерфейса G.703 приведены в таблице 3.6.1.

Таблица 3.6.1.

Скорость [кбит/с]	64	1544	6312	32064	44736	2048	8448	34368	139264	155520
Тип кода	AMI	AMI B8ZS	B6ZS	AMI	B3ZS	HDB3	HDB3	HDB3	CMI	CMI
Амплитуда, В	1,0	3,0	1,0	1,0	1,0	2,37 3,0	2,37	1,0	±0,55	±0,55
Ширина импульса, нс	15000	323,5	79	15,6	11,2	244	59,0	14,55	3,59	3,2

Кодировка относится лишь к случаю проводных каналов.

3.7 Дерево Штайнера Семенов ю.А. (гнц итэф)

Алгоритм дерева Штайнера используется в телекоммуникациях при оптимизации маршрутов передачи мультимедийных данных. Рассмотрим проблему поиска оптимального пути в предположении, что критерием оптимизации является длина этого пути. Задача может быть решена следующим образом:

1. Сначала находим два ближайших узла. Если соединение их не создаст циклических путей, производим такое объединение.

2. Повторяем операцию до тех пор, пока не будут объединены все узлы.

Алгоритм может быть упрощен. Сначала пометим все узлы уникальным образом. Затем находим два ближайшие узла с разными метками и соединяем их. После этого оба узла получают идентичные метки. Когда все узлы окажутся соединенными, они все получат идентичные метки. Имеется возможность добавления к графу дополнительных виртуальных точек Штайнера (1В), которые могут позволить сократить суммарную длину соединений. Смотри рис. 1 (http://www.colorstudy.com/static/ianb/old/steiner/summary.html; а также D. M. Warm, P. Winter, M. Zachariasen. Exact Algorithms for Plane Steiner Tree Problems: Computational Study, Advances in Steiner Trees, pages 81-116, Kluwer Academic Publishers, 2000; http://www.diku.dk/users/martinz/#publications).

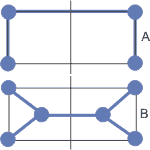
Рис.1. Пример уменьшения суммарной длины дерева путем введения дополнительных точек

Метрика дерева варианта А равна 4 (длина ребра ячейки имеет метрику 1), а варианта В 1+4*sqrt(1/2)=3,83. Вариант В на рисунке 1 не всегда реализуем, так как в некоторых случаях узлы Штайнера могут иметь только целочисленные координаты (х,у), тогда точки Штайнера не могут сократить длину соединений для графа на рис. 1. В этом варианте расстояние между узлами (x1,y1) и (x2,y2) равно abs(x1-x2)+abs(y1-y2). Пример использования точек Штайнера для такого варианта показан на рис. 2.

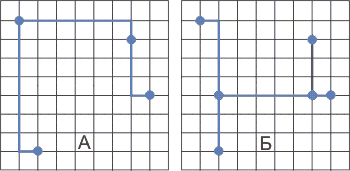
Рис. 2. Использование точек Штайнера для минимизации длины маршрута по ортогональной сетке

Дерево варианта А на рис. 2 характеризуется метрикой 19, а для Б после добавления двух точек Штайнера (выделены более светлой закраской) метрика равна 17.

Довольно часто (телекоммуникации, а также трассировка печатных плат и микросхем) приходится сталкиваться с проблемами поиска оптимальных деревьев Штайнера в плоскости (Эвклида и прямолинейный).

Проблема сводится к поиску наикратчайшей длины дерева Штайнера SMT (Shortest Minimum Tree). При этом приходится размещать набор из n терминалов на плоскости с учетом эвклидовой L₂-метрики и/или прямолинейной (или Манхэттеновской) L₁-метрики.

Пусть u=(u_x,u_y) и v=(v_x,v_y) являются парой точек на декартовой плоскости . Расстояние между этими точками в метрике L_p (L_p -расстояние, 1  p  ) характеризуется 2uv2_p= (|u_x - v_y|^p + |u_x - v_y|^p)^1/p.

Эвклидовские SMT (ESMT) и прямолинейные SMT (RSMT) представляют собой подмножества полных деревьев Штайнера (FST). Эвклидово FST (EFST) и прямолинейное FST (RFST), охватывающие k терминалов, 2 k  n, имеет k-2 точек Штайнера (за исключением случая k=4; RFST могут тогда иметь одну точку Штайнера с четырьмя исходящими ребрами). Точки Штайнера в EFST имеют три исходящих ребра. Точки Штайнера в RSMT имеют также три исходящих ребра (за исключением выше приведенного случая). Длина EMST (соответственно RMST) превосходит длину ESMT (соответственно RSMT) как минимум в 2/3 раз (соответственно 3/2 раз) [смотри F. K. Hwang, D. S. Richards and P. Winter. The Steiner Tree Problem. Annals of Discrete Mathematics 53. Elsevier Science Publishers, Netherlands, 1992.].

При поиске SMT для эвклидова или прямолинейного варианта субнаборы терминалов рассматриваются один за другим. Для каждого субнабора определяются все его FST один за другим. Кратчайшие из них запоминаются. Узким местом данного подхода является формирование FST.