3. Графический метод решения задач

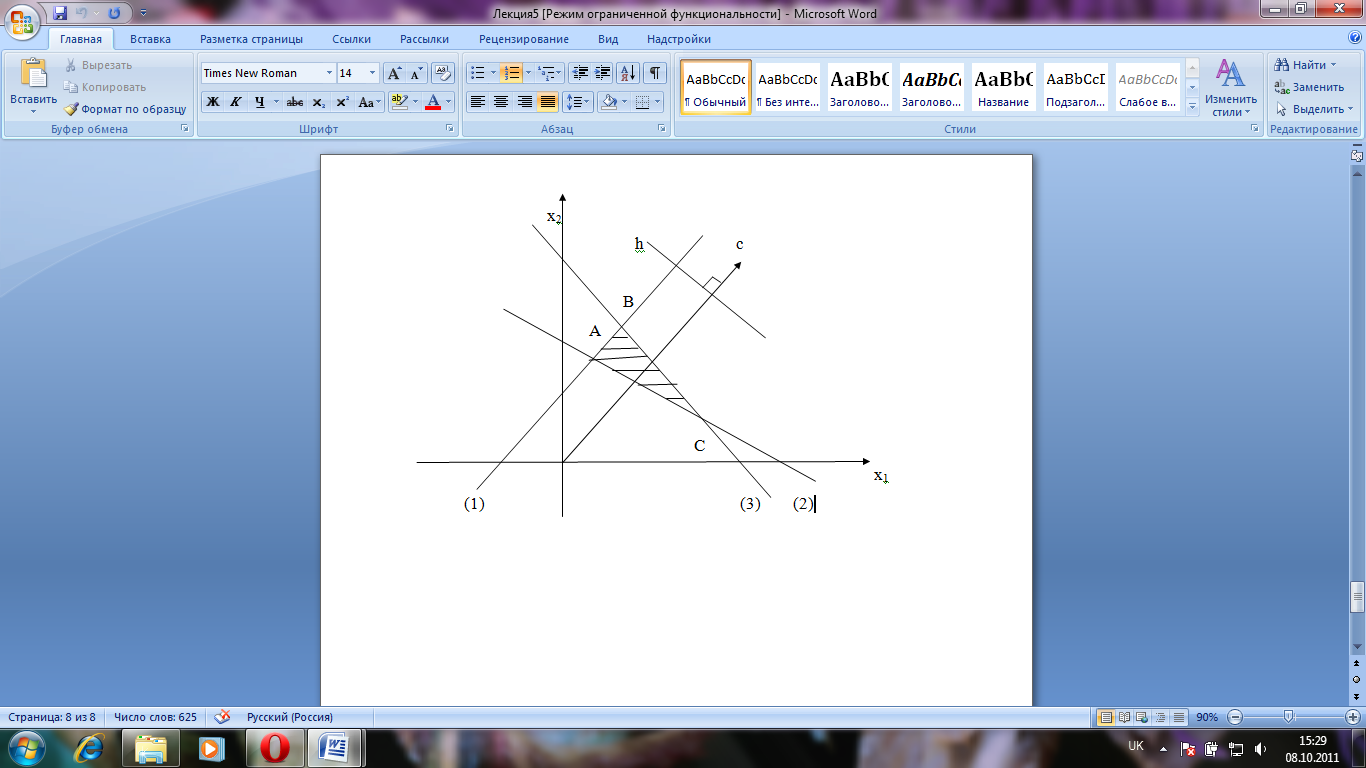
Задача 3.1

Решить графически

х1	0	3
х2	2	0

10х₁+15х₂=30

х1	0	5
х2	2	0

2х₁+5х₂=10

х1	0	5
х2	2,5	0

0,4х₁+0,8х₂=2

1. Построить графики:

х_опт=(3;0) находится в т.А

F=5*3+1*0=15.

Ответ: х*=(3;0), F=15.

А

Задача 3.2

Решить графически

Получилась задача в симметричном виде. Дальнейший алгоритм ее решения см. раньше.

х1	0	-3
х2	4,5	0

3х₁-2х₂=-9

х1	0	9
х2	6,75	0

3х₁+4х₂=27

х1	0	7
х2	14	0

-2х₁-х₂=-14

F= , X=

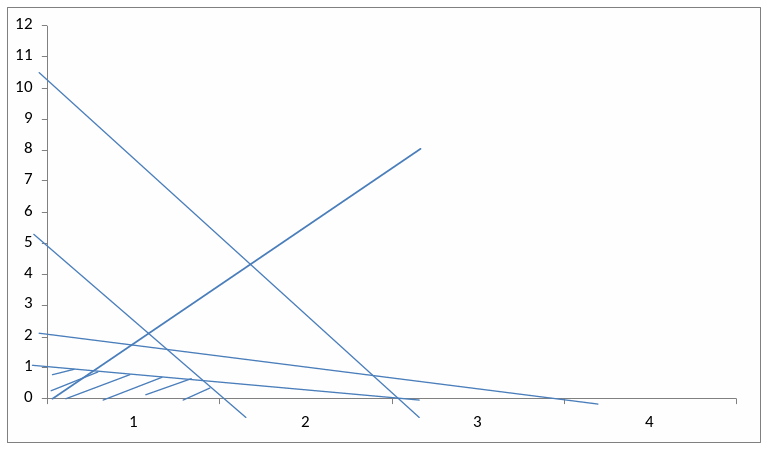
Задача 3.3

Решить графически

(1) (2) (3) (4)

	0	2
	10	0

	0	3
	2	0

	0	3
	5	0

	0	2
	1	0

Задача 3.4

Решить графически

Решение:

хj – к-во выпускаемой продукции

Графически:

1)(0;1,2); (2;0)

2)(0;2,8); (1,8;0)

3)(0;1,4); (2;0)

Ответ: F=(55,5)

X*=(1,7; 0,17)

Задача 3.5

Решить графически

Решение

1)(0;2); (2;0)

2)(0;2); (1;0)

3)(0;4); (2,6;0)

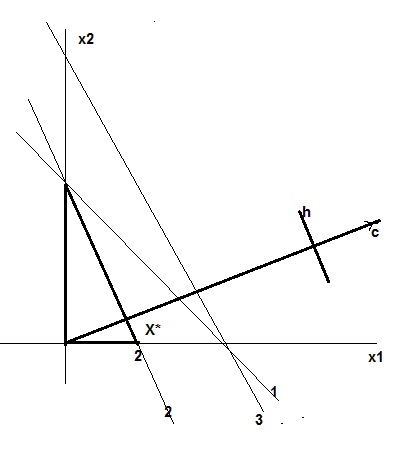
Ответ: F=(16)

X*=(2; 0)

Задача 3.6

Решить графически

Графически:

1)(0;10); (10;0)

2)(0;15); (7,5;0)

3)(0;10); (20;0)

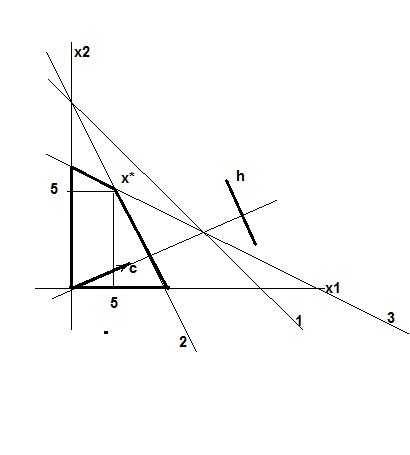
Ответ: F=(40)

X*=(5; 5)

Задача 3.7

Решить графически

F min =7x₁-x₂

Ограничения по запасам

x₁+x₂>=3 (0;3)(3;0)

5x₁+x₂>=5 (0;5)(1;0)

x₁+5x₂>=5 (0;1)(5;0)

x₁<=4 (4;0)

x₂<=4

Решение: (0;4)

Графический метод решения задачи

x ₁=0.2

x₂=4

F=7*0.2-4= -2.6

Ответ: F=-2.6; Х=(0,2; 4)

4.Метод потенциалов для нахождения оптимального плана, транспортная задача

Задача 4.1

Требуется перевезти продукцию от трех производителей, на три склада, если объёмы производства равны ai=(5,10,5), объёмы потребления bi=(10,5,2), стоимость перевозки единицы груза,

Cij=

П от-ль

Пр-во B1 B2 B3 B4

10 5 2 3

3 4 0

- - 2 3 2,0

A1 5 -q

4 6 4 0

A2 10 5 5 - -q - q 5,0

1 2 3 0

A3 5 5 - - - 0

5 0 0 0

ai bj; 20 17, задача не сбалансированная, открытая; нужно ввести потребителя B4.

F=2 2+3 0+5 4+5 6+5 1=59

3 4 2 0 0

4 6 4 0 2

1 2 3 0 -1

- j 2 4 2 0

Построим матрицу оценок , по формуле =(ui+(- j))-Cij.

-1 0 0 0

= 0 0 0 2 Q

0 1 -2 -1

Так как есть >0, то план не оптимален, приступим к его улучшению,max =2.

Среди клеток в которых max-Q, найдем minx , Q=(x-Qmin)=0.

Построим новую транспортную таблицу:

П от-ль

Пр-во B1 B2 B3 B4

3 4 2 0

- - 2 3

A1 -q

4 6 4 0

A2 5 5 5 - - q 0 q

1 2 3 0

A3 5 - - -

5 0 0 0

F=59 или F2=F1+A Q=53

Проверим план на оптимальность:

3 4 2 0 0

4 6 4 0 0

1 2 3 0 -3

- j 4 6 2 0

1 2 0 0

= 0 0 -2 0

0 1 -4 -3

Q=(x-Qmin)=3

П от-ль

Пр-во B1 B2 B3 B4

4 4 2

5 3 2

A 1

4 6 4 0

A2 5 2 - 3

1

A3 5

F3=59-2 3=53

3. 4 2 0 0

3. 6 4 0 2

1 2 3 0 -1

- j 2 4 2 -2