Министерство образования и науки, молодежи и спорта Украины
Одесский национальный политехнический университет
Институт бизнеса, экономики и информационных технологий
Кафедра экономической кибернетики и информационных технологий
Задачи
По курсу
«Исследование операций»
Одесса-2011-2012 (1 семестр)
Содержание
Введение в исследования операций………………………………………………...3
Решение задач линейного программирования. Симплекс-метод……………..4
Экономическая интерпретация симплекс-метода………………………………8
Решение задач линейного программирования М-методом…………………..9
Графический метод решения задач……………………………………………..12
Геометрические свойства задач линейного программирования…………….15
Алгоритм графического решения задач линейного
программирования, записанных в общем виде………………………………..18
Двойственные задачи линейного программирования……………………….26
Метод потенциалов для нахождения оптимального плана,
транспортная задача………………………………………………………….……32
9.Виды моделей транспортных задач…………………………………………...36
10. Целочисленное программирование……………………………………..…..37
11. Виды задач целочисленного программирования…………………………39
Симплекс-метод
Задача 1.1
9x1 + 10x2 + 16x3 → max;
Алгоритм:
№ |
|
|
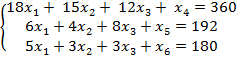
0 |
9 |
10 |
16 |
0 |
0 |
0 |
|
С |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
360 |
18 |
15 |
12 |
1 |
0 |
0 |
30 |
2 |
0 |
|
192 |
6 |
4 |
8 |
0 |
1 |
0 |
24 |
3 |
0 |
|
180 |
5 |
3 |
3 |
0 |
0 |
1 |
60 |
|
|
|
0 |
-9 |
-10 |
-16 |
0 |
0 |
0 |
|
1 |
0 |
|
72 |
9 |
9 |
0 |
1 |
- |
0 |
24 |
2 |
16 |
|
24 |
|
|
1 |
0 |
|
0 |
48 |
3 |
0 |
|
108 |
|
|
0 |
0 |
- |
1 |
72 |
|
|
|
384 |
3 |
-2 |
0 |
0 |
2 |
0 |
|
1 |
10 |
|
8 |
1 |
1 |
0 |
|
|
0 |
|
2 |
15 |
|
20 |
|
0 |
1 |
- |
|
0 |
|
3 |
0 |
|
96 |
|
0 |
0 |
|
|
1 |
|
|
|
F= |
400 |
5 |
0 |
0 |
|
|
0 |
|
Задача 1.2
Решить симплекс-методом
Симплекс-метод |
|
|
|
|
|
|
|
|
|
|
|
30 |
25 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
Q |
0 |
х3 |
6 |
3 |
5 |
1 |
0 |
0 |
2 |
0 |
х4 |
40 |
22 |
14 |
0 |
1 |
0 |
1 4/5 |
0 |
х5 |
20 |
10 |
14 |
0 |
0 |
1 |
2 |
|
F= |
0 |
-30 |
-25 |
0 |
0 |
0 |
|
|
|
|
30 |
25 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
Q |
0 |
х3 |
5/9 |
0 |
3 |
1 |
- 1/7 |
0 |
1/6 |
30 |
х1 |
1 4/5 |
1 |
2/3 |
0 |
0 |
0 |
2 6/7 |
0 |
х5 |
1 4/5 |
0 |
7 2/3 |
0 |
- 4/9 |
1 |
1/4 |
|
F= |
54 5/9 |
0 |
-6 |
0 |
1 3/8 |
0 |
|
|
|
|
30 |
25 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
|
25 |
х2 |
1/6 |
0 |
1 |
1/3 |
-0 |
0 |
|
30 |
х1 |
1 5/7 |
1 |
0 |
- 1/5 |
0 |
0 |
|
0 |
х5 |
1/2 |
0 |
0 |
-2 1/2 |
- 1/8 |
1 |
|
|
F= |
55 3/5 |
0 |
0 |
2 |
1 1/9 |
0 |
|
Задача 1.3
Решить симплекс-методом
|
|
|
9 |
8 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
Q |
0 |
х3 |
2 |
1 |
1 |
1 |
0 |
0 |
2 |
0 |
х4 |
2 |
2 |
1 |
0 |
1 |
0 |
1 |
0 |
х5 |
8 |
3 |
2 |
0 |
0 |
1 |
2 2/3 |
|
F= |
0 |
-9 |
-8 |
0 |
0 |
0 |
|
|
|
|
9 |
8 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
Q |
0 |
х3 |
1 |
0 |
1/2 |
1 |
- 1/2 |
0 |
2 |
9 |
х1 |
1 |
1 |
1/2 |
0 |
1/2 |
0 |
2 |
0 |
х5 |
5 |
0 |
1/2 |
0 |
-1 1/2 |
1 |
10 |
|
|
9 |
0 |
-3 1/2 |
0 |
4 1/2 |
0 |
|
|
F= |
9 |
0 |
-3 1/2 |
0 |
4 1/2 |
0 |
|
|
|
|
9 |
8 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
|
8 |
х2 |
2 |
0 |
1 |
2 |
-1 |
0 |
|
9 |
х1 |
0 |
1 |
0 |
-1 |
1 |
0 |
|
0 |
х5 |
4 |
0 |
0 |
-1 |
-1 |
1 |
|
|
F= |
16 |
0 |
0 |
7 |
1 |
0 |
|
Задача 1.4
Решить симплекс-методом
|
|
|
5 |
3 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
Q |
0 |
х3 |
10 |
1 |
1 |
1 |
0 |
0 |
10 |
0 |
х4 |
15 |
2 |
1 |
0 |
1 |
0 |
7 1/2 |
0 |
х5 |
20 |
1 |
2 |
0 |
0 |
1 |
20 |
|
F= |
0 |
-5 |
-3 |
0 |
0 |
0 |
|
|
|
|
5 |
3 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
Q |
0 |
х3 |
2 1/2 |
0 |
1/2 |
1 |
- 1/2 |
0 |
5 |
5 |
х1 |
7 1/2 |
1 |
1/2 |
0 |
1/2 |
0 |
15 |
0 |
х5 |
12 1/2 |
0 |
1 1/2 |
0 |
- 1/2 |
1 |
8 1/3 |
|
|
37 1/2 |
0 |
- 1/2 |
0 |
2 1/2 |
0 |
|
|
F= |
37 1/2 |
0 |
- 1/2 |
0 |
2 1/2 |
0 |
|
|
|
|
5 |
3 |
0 |
0 |
0 |
|
с |
б |
а0 |
а1 |
а2 |
а3 |
а4 |
а5 |
|
3 |
х2 |
5 |
0 |
1 |
2 |
-1 |
0 |
|
5 |
х1 |
5 |
1 |
0 |
-1 |
1 |
0 |
|
0 |
х5 |
5 |
0 |
0 |
-3 |
1 |
1 |
|
|
F= |
40 |
0 |
0 |
1 |
2 |
0 |
|