2. Кинематический расчет привода

2.1 Определение показателя геометрического ряда чисел оборотов шпинделя.

Показатель геометрического ряда чисел оборотов шпинделя подсчитывается по формуле : , где

n_max – максимальная частота вращения шпинделя,

n_min – минимальная частота вращения шпинделя,

z – число скоростей.

В нашем случае : z = 12, n_max = 1180, n_min = 95.

Тогда получим: =1,257 – округлим до 1,26 .

Примем стандартные значения показателя ряда φ = 1,26. Запишем для него 12 нормальных значений чисел оборотов шпинделя: n₁ =95,

n₂ = 80; n₃ = 100, n₄ = 125, n₅ = 160, n₆ = 200, n₇ = 250, n₈ = 315, n₉ = 400,

n₁₀ = 500, n₁₁ = 630, n₁₂ = 800.

2.2 Выбор структуры привода.

2.2.1 Структурная формула

Применяемой кинематической схеме соответствует структурная формула, показывающая как разбито общее количество вариантов чисел оборотов между отдельными группами передач, т.е.

z = P₁·P₂·P₃·…·P_n, где

P₁ – число скоростей первой группы передач,

P_n – число скоростей n-ой группы передач.

В нашем случае имеем:

12 = 3(1)·2(3)·2(6)

2.2.2 Развернутые структурные формулы

Промежуточные значения передаточных отношений или чисел оборотов шпинделя могут быть получены путем различных комбинаций передач в группах P₁,P_2,P₃…P_n в зависимости от принятого порядка перемещений групп передач, т.е. от того, какая группа передач принята основной, какая первой умножающей, какая второй умножающей и т.д. Передаточные отношения в коробках скоростей строятся по закону геометрического ряда. Передаточные отношения в каждой группе передач также образуют геометрический ряд, но с показателем φ^x, где x – у каждой группы передач свой.

Для основной группы передач x = x₀ = 1; для первой умножающей x = x₁ = P₀·P₁, т.е. числу ступеней основной группы передач; для второй умножающей x = x₂ = P₀·P₁·P₂·…·P_k-1.

На основании изложенного составим для конкретных условий развернутые структурные формулы, отражающие различный порядок переключения групп передач.

Общий вид формулы: z = P₁(x₁)·P₂(x₂)·…·P_n(x_n)

Для нашего случая: 12 = 3(1) ·2(3) ·2(6),

2.2.3 Построение структурных сеток

С целью наглядного представления и выбора оптимальной структуры привода изобразим некоторые возможные структурные сетки для принятой кинематической схемы.

Сетка №1 Сетка №2

3(1) 2(3) 2(6) 3(1) 2(3) 2(6)

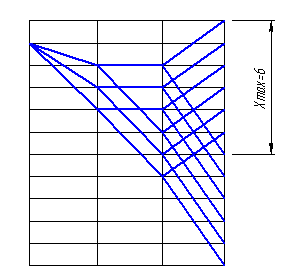
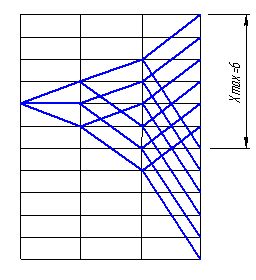
Рис. 1

2.2.4 Анализ структурных сеток.

Не все варианты структурных сеток позволяют получить при разработке коробки скоростей компактное конструктивное решение. Это зависит от наибольшего значения показателя ряда, допускаемого той или иной сеткой. Для коробок скоростей установлены рекомендуемые значения передаточных отношений для любой группы передач: i_min = , i_max = 2.

При выполнении этих условий получаем выражение для φ_max

φ_max = , где x_max – число интервалов по сетке между двумя крайними лучами последней умножающей группы.

Для сетки №1 x_max = 6, φ_max = =1,26;

Для сетки №2 x_max = 6, φ_max = =1,26.

Значит, для двух сеток можно разработать конструкцию коробок скоростей со стандартными значениями показателей – 1,06; 1,12; 1,19; 1,26; 1,3; 1,41.

Все рассмотренные сетки отвечают условию φ ≤ φ_max – условию компактного исполнения привода.

Из двух вариантов выбираем наилучший по конструктивным соображениям. Наиболее оптимальной является сетка №1, т.к. в приводах главного движения происходит уменьшение чисел оборотов от ведущего вала к ведомому. При применении данной сетки в области высоких чисел оборотов работает большое количество шестерен, т.к. главная редукция осуществляется на последующей ступени. Скоростные шестерни и валы имеют меньшие габариты, т.к. при данной мощности они будут придавать меньшие крутящие моменты, а следовательно привод будет более компактным, чем в других случаях.