Завдання 12.

На основі даних підприємства визначити залежність отриманого прибутку від обсягу реалізації продукції, використавши методи кореляційно-регресійного аналізу, за умови, що форма зв'язку є лінійною. Оцінити отримане рівняння регресії. Зробити висновки за результатами аналізу (інформацію наведено в дод. 12).

№ під-ва	Х рентабельність	У прибуток	Х*У	Х2	Ух
1	389	15,1	5873,9	151321	11,9
2	417	16,0	6672	173889	15,4
3	409	15,6	6380,4	167281	14,4
4	431	16,4	7068,4	185761	17,1
5	430	16,0	6880	184900	16,9
6	440	16,3	7172	193600	18,2
Разом	2516	95,4	40046,7	1056752	93,8

Якісний та графічний аналіз даних (див. рисунок) дає підстави обрати прямолінійну залежність між цими показниками, яка має загальний вигляд:

y_x= a₀ + a_1*x

де: y_x - результативна ознака (продуктивність праці); х - факторна ознака (електроозброєність праці).

Залежність буде визначена і модель залежності побудована, коли будуть визначені параметри а₀ та а₁. Щоб їх відшукати потрібно скласти систему нормальних рівнянь, для чого виконуємо необхідні обчислення в таблиці.

Система нормальних рівнянь:

Розв’язком її є: a₀ = -35,52; a₁ = 0,122.

Отже, рівняння кореляційного зв’язку має вигляд:

у_х=-35.52+0,122х.

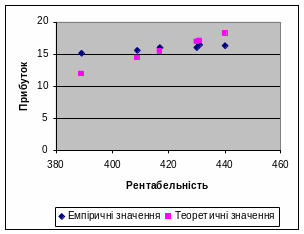
Коефіцієнт регресії а₁ показує, що в разі зміни рентабельності на 1 пункт прибуток підприємства в даній сукупності змінюється на 0,122.

Завдання 15.

Виходячи з наведених даних вирівняти динамічний ряд, який характеризує реалізацію продукції підприємства промисловості, дати оцінку рівнянню регресії та спрогнозувати обсяг реалізації на наступний рік (інформацію наведено в дод. 15).

Роки (Х)	Обсяг реалізації, тис. грн. (У)	Х*У	Х2	Ух, вирівняний ряд
1	550	550	1	540,7
2	551,2	1102,4	4	551,286
3	552,4	1657,2	9	561,872
4	554,8	2219,2	16	572,458
5	597,6	2988	25	583,044
6	600	3600	36	593,63
7	601,2	4208,4	49	604,216
Σ = 28	4007,2	16325,2	140	4007,206

а₀ = (∑у*∑х² - ∑ху*∑х) / (n ∑х² - ∑х*∑х)

а₁ =(n*∑ху -∑х*∑у) / (n ∑х² - ∑х*∑х)

а₀ = (4007,2*140-16325,2*28)/(7*140-28*28) = 103902,4/196 = 530,114

а₁ = (7*16325,2-28*4007,2)/(7*140-28*28) = (114276,4-112201,6)/196=10,586

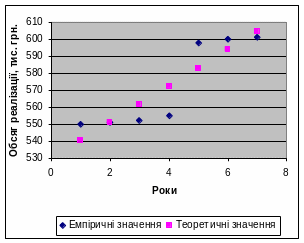
Отже, лінійне рівняння регресії має вигляд:

Y_х = 530,114 + 10,586*х

Спрогнозуємо за отриманим рівнянням регресії обсяг реалізації продукції у 8-му році: У (8 рік) = 530,114 + 10,586*8 = 614,802 тис.грн. Ці прогнозні значення навряд чи можна вважати достовірними, тому що коефіцієнти детермінації та кореляції відповідають дуже слабкому рівню зв’язку між змінними.

Дане рівняння регресії показує, що з кожним наступним роком обсяг реалізації зросте на 10,586 тис. грн.