Решение систем линейных уравнений

1) Определение матрицы, ее виды (квадратная, прямоугольная и т.Д.). Операции сложения, вычитания матриц, умножение на число.

Матрицей называется квадратная или прямоугольная таблица, заполненная числами. Эти числа называются элементами матрицы. Элементы матрицы, расположенные по горизонталям, образуют строки матрицы. Элементы матрицы, расположенные по вертикалям, образуют столбцы матрицы. ŒМатрица A , имеющая m строк и n столбцов, называется матрицей размера m на n. ______________________________________________________________________________

Каждую матрицу можно умножить на любое число, причем, если k– число, то k*A= {k*aij }.

________________________________________________________________________________

Матрицы одного и того же размера можно складывать, причем Am*n *Bm*n= {aij +bij}

2) Операция умножения матриц и ее свойства. Транспонирование матриц и его свойства.

Умножение:    Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй:

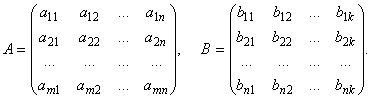
    Произведением матриц A и B  называется матрица

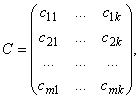
    элементы которой вычисляются по формуле

,

    __________________________________________________________________________

Транспонированием матрицы называется замена строк матрицы на её столбцы с сохранением их номеров. Транспонированная матрица обладает следующими свойствами: -дважды транспонированная матрица равна исходной матрице, т.е. (А^T)^T=A; -при транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций; -симметрическая матрица не изменяется при транспонировании.

3) Определитель матрицы и его свойства. Понятие линейной зависимости.

Каждой такой матрице можно поставить в соответствие единственное действительное число, называемое определителем (детерминантом) матрицы и обозначаемое

 Для каждой квадратной матрицы определено число, называемое определителем матрицы.

Определителем матрицы первого порядка  называется число, равное единственному

элементу этой матрицы: A = {a}, detA = |A| = a.

Пусть A — произвольная квадратная матрица порядка n, n>1:

Определителем квадратной матрицы n-го порядка, n >1, называется число, равное

где M_1j — определитель квадратной матрицы, полученной из матрицы A вычеркиванием

первой строки и j-го столбца.

Квадратная матрица называется вырожденной, если её определитель равен нулю.

Квадратная матрица называется невырожденной, если её определитель отличен от нуля.

Определитель произведения квадратных матриц равен произведению определителей

сомножителей.

Отметим, что определитель существует только для квадратных матриц.

4) Элементарные преобразования. Дополнительный минор, минор, алгебраическое дополнение.

Элементарными преобразованиями матрицы называют следующие операции:

-перестановка любых двух строк матрицы;

- умножение любой строки на произвольное, отличное от нуля, число;

- сложение любой строки с другой строкой , умноженной на произвольное число;

- транспонирование матрицы.

______________________________________________________________________

Рассмотрим матрицу A:

  

Вычеркнем из матрицы k строк с номерами i₁, i₂, ..., i_k и k столбцов, с номерами j₁, j₂, ..., j_k.

Элементы, расположенные на пересечении вычеркнутых строк, образуют определитель,

который называется минором порядка k. Его обозначают M_k:

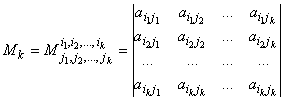
Минор, образованный оставшимися элементами называется дополнительным минором минора M_k и обозначают M_k'.

Алгебраическим дополнением A_k минора M_k называется число, равное дополнительному

минору M_k', умноженному на (−1) в степени, равной сумме номеров вычеркнутых строк и

столбцов:

Если вычеркнуты одна строка и один столбец, то соответствующие миноры и алгебраические дополнения называют минорами и алгебраическими дополнениями элемента.