Вариант 24.

а) Вычислить: s=bSIN(ax²COS(2x))-1

где b=Ln(a)- при x=1.8, a=2.1

б) Вычислить:

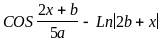		, если ax>b
y=		e3x-0.89SIN(x), если ax=b
		Arctg(2x)+bCOS(2ax), если ax<b

при a= -2.391, b=7.08, x=0.023

в) Представить таблицу значений аргумента и заданной функции.

		2t-a, если t>=4
y=
		bet+t, если t<4

где a=Ln(t²+2t+5), b=COS²(t)-SIN(t)

для t[2;6] с шагом 0.5

Вариант 25.

а) Вычислить: y=Lnx/a+SIN(x+0.3)^1/2

где a=e^-bx-Tg(b+x) при x= -0.41, b=0.5

б) Вычислить:

		Ln(bx)-1/(bx+1), если SIN(bx)<0.75
z=		bx+1, если SIN(bx)=0.75
		Ln(bx)+1/(bx+1), если SIN(bx)>0.75

для b=1.38, x=5.83

в) Вычислить:

		2Lnt+b, если t+b<0
x=
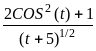		, если t+b>=0

		tb, если x3>1
y=
		Lnx3, если x3< =1

для t[-2.8;-2] с шагом 0.1, b=2.2